贡献者: addis; ACertainUser
复变函数(complex function)一般是指自变量和函数值都在复数域内取值的函数,即 $f:\mathbb C \to \mathbb C$,通常表示为
\begin{equation}
w = f(z)~.
\end{equation}
更一般地,函数值为复数的函数都可以叫做复变函数。例如 $f: \mathbb R \to \mathbb C$(自变量是一个实数)或者 $f:\mathbb R^N \to \mathbb C$(自变量是 $N$ 个有序实数)。
1. 复变函数的表示方法
z 型
完全类似于一元实函数 $y=f(x)$,复函数可以记为
\begin{equation}
w = f(z)~.
\end{equation}
其中 w,z 都是复数。例如 $w=e^z, w=2z+i$ 等。
x-y 型
若把自变量 $z$ 拆分成实部 $x$ 和虚部 $y$,即 $z = x + \mathrm{i} y$,且函数 $f$ 也拆分成实部函数 $u(x,y)$ 和虚部函数 $v(x,y)$,则复变函数可记为两个二元实函数的 “组合”,即
\begin{equation}
w = u(x,y) + \mathrm{i} v(x,y)~,
\end{equation}
其中 $u, v: \mathbb R^2 \to \mathbb R$ 都是二元实函数。
例如,复指数函数被定义为
\begin{equation}
w = \mathrm{e} ^z = \mathrm{e} ^x \cos y + \mathrm{i} \mathrm{e} ^x\sin y \qquad (z \in \mathbb C)~,
\end{equation}
即实部和虚部函数分别为 $u(x, y) = \mathrm{e} ^x \cos y$,$v(x, y) = \mathrm{e} ^x \sin y$。
例 1 简谐振动的复数形式
例如物理中质点的简谐振动的复数形式为
\begin{equation}
f(t) = \mathrm{e} ^{- \mathrm{i} \omega t} = \cos\left(\omega t\right) + \mathrm{i} \sin\left(\omega t\right) \qquad (t \in \mathbb R)~.
\end{equation}
它的实部表示振动的位移,而虚部没有物理意义。
2. 复变函数与矢量场
当我们把复变函数记为式 3 的形式后,可以把它看作一个平面矢量场,即复平面上的每一点对应一个几何矢量。令实轴和虚轴分别为 $x$ 轴和 $y$ 轴,其单位矢量分别为 $ \hat{\boldsymbol{\mathbf{x}}} $ 和 $ \hat{\boldsymbol{\mathbf{y}}} $,令位置矢量 $ \boldsymbol{\mathbf{r}} = x \hat{\boldsymbol{\mathbf{x}}} + y \hat{\boldsymbol{\mathbf{y}}} $,那么这个矢量场就可以表示为
\begin{equation}
\boldsymbol{\mathbf{w}} ( \boldsymbol{\mathbf{r}} ) = u( \boldsymbol{\mathbf{r}} ) \hat{\boldsymbol{\mathbf{x}}} + v( \boldsymbol{\mathbf{r}} ) \hat{\boldsymbol{\mathbf{y}}} ~.
\end{equation}
这相当于把映射 $f:\mathbb C \to \mathbb C$ 看成 $f: \mathbb R^2 \to \mathbb R^2$。其中 $u, v$ 分别是二维平面上的标量场。
正因如此,研究复变函数时可以借助许多矢量分析的工具,如散度和旋度等。所以以后讲解时我们也会使用相应的矢量分析内容作为预备知识。
3. 复变函数的可视化
使用矢量场的概念可以用于把复变函数可视化,这里以复指数函数(式 4 )为例。第一种方法是用箭头表示平面矢量场,如图 1 。
图 1:$ \mathrm{e} ^z$ 对应的二维矢量场(
式 6 ),图中的箭头与 $ \boldsymbol{\mathbf{w}} ( \boldsymbol{\mathbf{r}} )$ 成正比。
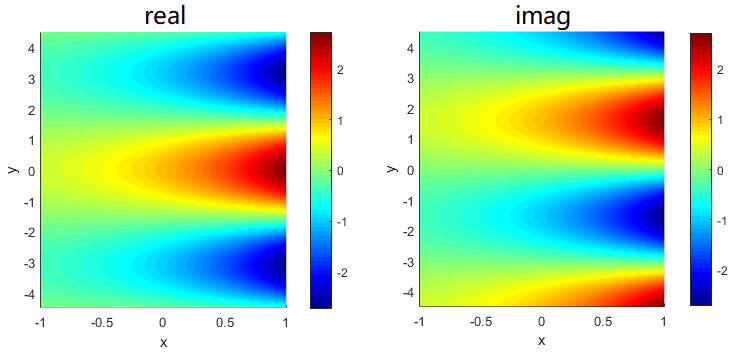
也可以把复变函数的实部 $u(x,y)$ 和虚部 $v(x, y)$ 分别画成二维标量场(图 2 )。
图 2:$ \exp\left(z\right) $ 的实部和虚部函数
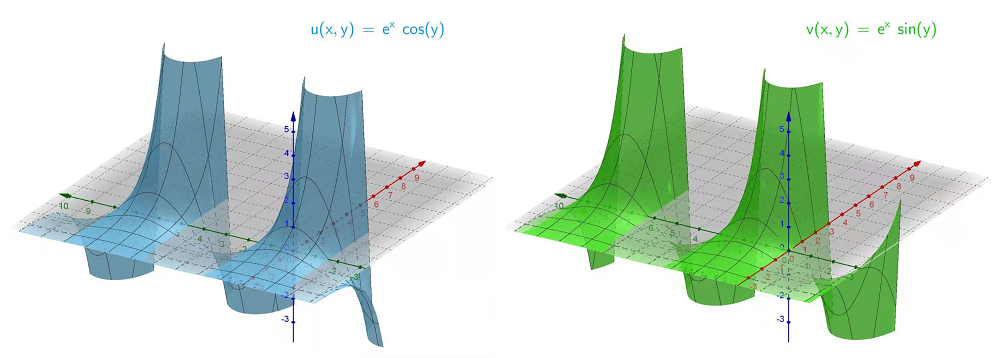
式 3 也可以画成 3D 的曲面图
图 3:$ \exp\left(z\right) $ 的实部和虚部函数
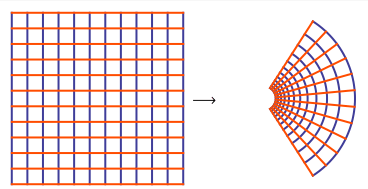
还有一种方式是使用变形网格的方式表示平面到平面的映射(图 4 ),由该图可以看出 $x$ 决定 $ \mathrm{e} ^z$ 的模长,$y$ 决定 $ \mathrm{e} ^z$ 的辐角。
图 4:$ \exp\left(z\right) $ 函数把复平面上的方形网格映射成另一种形状的网格(来自 Wolfram Alpha)
4. 作为实函数的拓展
复变函数中很多函数与我们原来学过的函数同名,只是定义域和值域从实数拓展到了复数。例如三角函数,对数函数,指数函数等。拓展后,复变函数的定义必须要与原来的实函数保持 “兼容”,即当自变量取实数时,函数值也要与原来相同。
例如,当复指数函数式 4 的自变量只在实轴上取值(即 $y = 0$)时,该函数变为我们原来所熟悉的实函数 $ \mathrm{e} ^x$。 又如,复正弦函数的定义为
\begin{equation}
\sin z = \sin\left(x + \mathrm{i} y\right) = \sin x\cosh y + \mathrm{i} \cos x\sinh y~,
\end{equation}
其中 $\sinh $ 和 $\cosh $ 是双曲正弦和双曲余弦函数
双曲函数。当 $y = 0$ 时($\cosh 0 = 1$,$\sinh 0 = 0$),又重新得到实函数 $\sin x$。
如果只需满足 “兼容” 的条件,那么拓展的方式可以有无限多种,所以为什么一定要拓展成式 4 或式 7 呢?这是因为我们通常还需要复变函数满足另一个条件,就是拓展后的函数需要是解析的,这叫做解析拓延。解析拓延是唯一的,例如实函数 $\sin x$ 进行解析拓延后,只有式 7 一种可能的定义。
我们研究的复变函时几乎都是在讨论解析函数(至少在复平面的某个区域内解析),简单来说解析函数要求它可以在复平面的某个区域内关于某点 $z_0$ 展开为(复)无穷级数(类比实函数的泰勒级数)
\begin{equation}
f(z) = \sum_{n=0}^\infty c_n (z - z_0)^n~.
\end{equation}
我们说,如果复变函数在某个区域解析,那么它在该区域就是
光滑(smooth)的,即无穷阶连续可导(类比实函数的
高阶导数)。
5. 复变函数的导数
复变函数的导数定义与实函数的导数十分相似:
\begin{equation}
f'(z) = \lim_{\Delta z \to 0} \frac{\Delta f}{\Delta z}~.
\end{equation}
只是这里的除法变为复数的除法(
式 20 )。讨论一般复变函数的导数较为复杂,因为它不但取决于 $z$ 的值,还取决于求导的方向(即 $\Delta z$ 趋近于 $0$ 的方向),这有点类似于
方向导数。但我们通常研究的解析函数有一个非常好的性质:如果复变函数在某个区域上解析,那么在该区域上其导数与求导方向无关。详见 “
柯西—黎曼条件”。
对于复数域的基本初等函数(几乎都是解析函数),它们的导函数也大多和实数域基本初等函数的导函数具有一样的表达式。例如 $( \mathrm{e} ^z)' = \mathrm{e} ^z$,$\sin' z = \cos z$,等。四则运算的求导法则也与实函数的情况相同。
6. 复积分
复变函数的积分需要在复平面上选取一个路径。从矢量场的角度考虑,这可以类比矢量场的线积分。
未完成:旋度为零,积分结果与路径无关