贡献者: ACertainUser; addis; JierPeter; Giacomo
1. 一点处的导数
几何含义
12一个一元函数 $y = f(x)$ 在直角坐标系中表示为一条曲线。在切线与割线中,我们已经初步了解了什么是切线与割线。
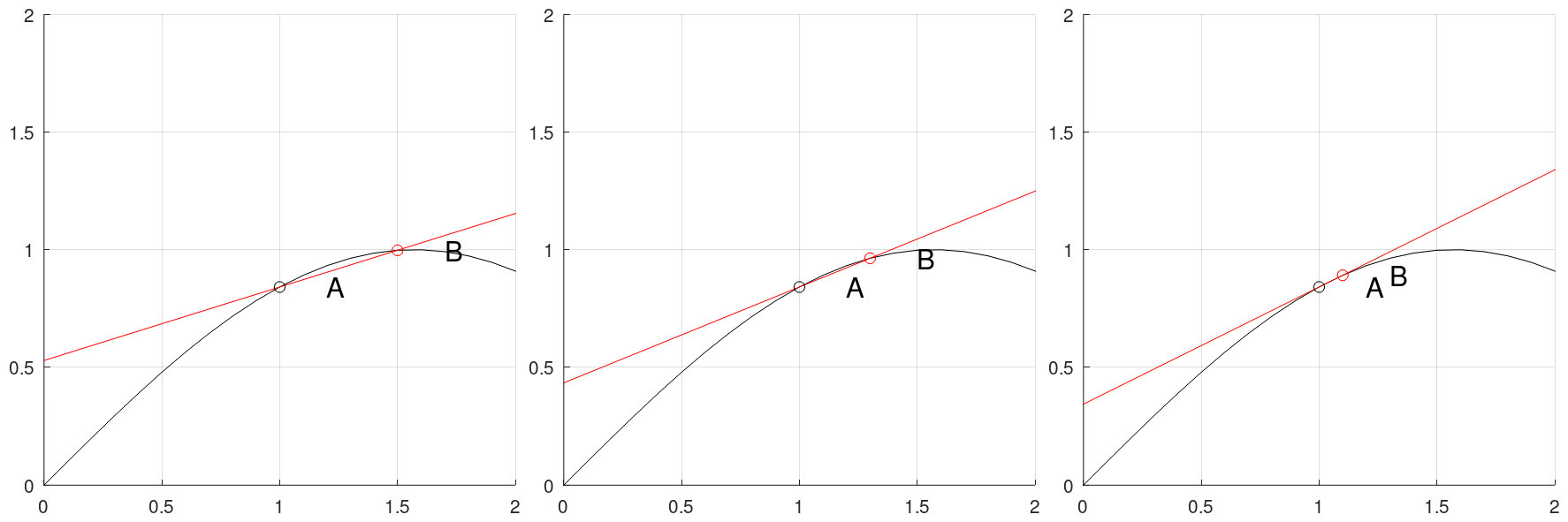
图 1:B 趋向 A,割线趋向切线
我们先写出割线的直线方程。由于割线就是一条经过 A,B 两点的直线,根据高中数学知识,很容易得到
\begin{equation}
y-y_A=\frac{y_B-y_A}{x_B-x_A}(x-x_A)=\frac{f(x_B)-f(x_A)}{x_B-x_A}(x-x_A)~.
\end{equation}
观察割线的方程,除了斜率项 $k=\frac{f(x_B)-f(x_A)}{x_B-x_A}$,其余项均与 $x_B$ 无关。现在,如图 1 所示,我们固定 A 点不动,让 B 点趋近于 A 点,即令 $x_B\rightarrow x_A$,这使割线趋向于切线,它的斜率即可用极限来定义
\begin{equation}
k=\lim_{x_B\to x_A}\frac{f(x_B)-f(x_A)}{x_B-x_A}~.
\end{equation}
我们把这个切线的斜率定义为 $x=x_A$ 处 $f(x)$ 的导数,一般记为 $f'(x_A)$ 或 $ \frac{\mathrm{d}{f}}{\mathrm{d}{x}} |_{x=x_A}$。因此,我们说函数一点处的导数值就等于这点处切线的斜率。
图 2:点 $A$ 的切线。$f'(x_A)=k=\tan \theta$
更一般的,有
定义 1 函数一点处的导数
$f(x)$ 在 $x=x_0$ 处的导数为
\begin{equation}
f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}~,
\end{equation}
也可以写为
\begin{equation}
f'(x_0)=\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}~.
\end{equation}
“物理” 含义
仔细观察 $x=x_0$ 附近切线的形状与 $f(x)$ 的形状,你很容易看出这两者是几乎一样的3,这启发我们在一个小区域内用切线来近似原函数。
图 3:将切点放大,会发现切线和曲线在切点附近 “重合”
此时,若想计算 $x$ 轻微增加后,函数值 $y$ 的增量,就没有必要复杂地计算
$$\Delta y = f(x_0+\Delta x) - f(x_0)~,$$
而只需要计算
\begin{equation}
\Delta y = f'(x_0) \Delta x~,
\end{equation}
这就引入了
微分的概念。更重要的是,这启发了我们导数的另一层含义:导函数确定了 $x=x_0$ 处,$y$ 关于 $x$ 变化的 “敏感度”,即 $x$ 轻微变化时,$y$ 会做出多大的响应。例如,一个绝对值大的导数值意味着 $y$ 会因为 $x$ 的轻微变化而剧烈变化。
理解这一含义的最直白例子或许是速度,速度被定义为物体位置关于时间的导数 $v= \frac{\mathrm{d}{r}}{\mathrm{d}{t}} $。即使只靠直觉,我们也能理解“速度快” 就是指 “一瞬间他就从我眼前飞过去了”,这就是说当时间轻微增加时,物体的位置大幅变化。
单侧导数
类似于单侧极限,我们也可以引入单侧导数的概念。如果 B 点从右侧趋近 A 点,但始终不运动到 A 点的左侧,那么此时切线的斜率即为该点处函数的右导数值,可以记为 $f'_+(x_A)$。更一般地,用极限的语言可以写为:
定义 2 单侧导数
$f(x)$ 在 $x=x_0$ 处的右导数为:
\begin{equation}
f'_+(x_0) = \lim_{x\to x_0^+} \frac{f(x)-f(x_0)}{x-x_0}~.
\end{equation}
同理,可以定义左导数:
\begin{equation}
f'_-(x_0) = \lim_{x\to x_0^-} \frac{f(x)-f(x_0)}{x-x_0}~.
\end{equation}
类似于极限,我们也有
定理 1
函数在某点可导的充分必要条件是它左右导数都存在并相等。
$$f'(x_0)=A\Longleftrightarrow f'_+(x_0)=f'_-(x_0)=A~.$$
也就是说,若左(或右)导数不存在,或者左、右导数存在但不相等,那此处的导数就不存在。
例 1
如图,在棱角处,虽然函数连续,甚至左、右导数均存在,但他们的大小不相同,因此在棱角处该函数不可导。
图 4:棱角处不可导
一个更明确的例子是绝对值函数 $f(x) = |x|$, 它在零点的左导数为 $-1$,而右导数为 $1$。
未完成:作图:函数图像和导函数图像
。
2. 导函数
在上文中,我们定义了一点处函数的导数。原则上我们可以任意选取函数定义域中的一点,然后用根据上文 “导数的定义” 找到该点处的导数值。这也就是说,对于函数定义域中的任意一点,都有一个导数值与之对应,这符合函数的定义,也就是说我们可以在这二者间定义一个新函数,这就是 $f(x)$ 的 “导函数”;在不引起混淆的情况下往往简称为 “导数”。
字面上看,导函数的定义与一点处函数的导数完全类似。
定义 3 导函数
\begin{equation}
f'(x)=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}~.
\end{equation}
通常将导函数记为以下的一种
\begin{equation}
f'(x),\quad [f(x)]',\quad \frac{\mathrm{d}{y}}{\mathrm{d}{x}} ,\quad \frac{\mathrm{d}{f}}{\mathrm{d}{x}} ,\quad \frac{\mathrm{d}}{\mathrm{d}{x}} f(x)~.
\end{equation}
在物理中,还可以在物理量上方加一点表示对时间求导(注意仅限于对时间求导),例如 $\dot f(t) = \mathrm{d}{f(t)}/\mathrm{d}{t} $。
例 2 直线方程的导函数
计算 $f(x)=2x+3$ 的导函数。
根据定义,
$$
\begin{aligned}
f'(x)&=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\\
&=\lim_{\Delta x \to 0}\frac{[2(x+\Delta x)+3]-(2x+3)}{\Delta x}\\
&=\lim_{\Delta x \to 0}\frac{2\Delta x}{\Delta x}\\
&=2~.
\end{aligned}
$$
事实上,所有直线方程的导函数都是常函数,且数值上等于自己的斜率。当然,实际上很少直接使用定义计算导数,有一些技巧可以简化求导过程(见本节其他文章)。
例 3 常函数的导函数
计算 $f(x)=C$ 的导函数, 其中 $C$ 是常数。
仍然根据定义,
$$
\begin{aligned}
f'(x)&=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\\
&=\lim_{\Delta x \to 0}\frac{C-C}{\Delta x}\\
&=\lim_{\Delta x \to 0}\frac{0}{\Delta x}\\
&=0~,\\
\end{aligned}
$$
因此常函数的导数为零。这可以理解为例 2 当 $x$ 的系数为零时的特例。
例 4 二次函数的导函数
计算 $f(x)= a x^2 + b x + c$ 的导函数。
仍然根据定义,
$$
\begin{aligned}
f'(x)&=\lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} \\
&=\lim_{\Delta x \to 0} \frac{a(x + \Delta x)^2 + b (x + \Delta x) + c - a x^2 - b x - c}{\Delta x} \\
&=\lim_{\Delta x \to 0} \frac{2 a x (\Delta x) + a (\Delta x)^2 + b \Delta x}{\Delta x} \\
&=\lim_{\Delta x \to 0} 2 a x + a (\Delta x) + b \\
&= 2 a x + b ~,\\
\end{aligned}
$$
因此二次函数的导数为一次函数。当 $a = 0$,二次函数退化为直线方程。
1. ^ 本文参考了 [1] , [2]
2. ^ 除非特别声明,我们暂且假定探讨的函数在定义域内处处可导,就和大多数物理学家和工程师所默许的一样
3. ^ 这个结论可不是我瞎说的,数学上是能给出严格的证明
[1] ^ 同济大学数学系. 高等数学 (上下册) 高等教育出版社 (2014) 第七版
[2] ^ J. Hass, C. Heil, M. Weir.Thomas' Cauculus 14ed