氦原子数值解 TDSE

贡献者： addis

预备知识　广义球谐函数，Lanczos 算法，氢原子球坐标薛定谔方程数值解

1. 波函数展开

　　使用角向基底为两个电子总轨道角动量和 $z$ 分量的本征态，即广义球谐函数 $Y_{l_{1}, l_{2}}^{L, M} ({\hat{r}}_{1}, {\hat{r}}_{2})$ 。

　　总波函数所在的空间可以看做角向空间和径向空间的张量积空间。现在有了角向空间的正交归一基底（内积由式 12 定义为 $\int \dots d Ω_{1} d Ω_{2}$ ），总波函数就可以在该基底上展开（ $| R_{λ} ⟩$ 并不是基底也非正交归一，只相当于展开系数）

\begin{matrix} (1) & | Ψ ⟩ = \sum_{λ} | R_{λ} ⟩ \otimes | Y_{λ} ⟩ . \end{matrix}

其中

λ

是将所有的

(l_{1}, l_{2}, L, M)

组合排序后的序号。

| R_{λ} ⟩

是二维径向波函数

\begin{matrix} (2) & | R_{λ} ⟩ = \frac{1}{r_{1} r_{2}} ψ_{λ} (r_{1}, r_{2}) . \end{matrix}

即总波函数为

\begin{matrix} (3) & Ψ (r_{1}, r_{2}) = \sum_{L, M, l_{1}, l_{2}} \frac{1}{r_{1} r_{2}} ψ_{l_{1}, l_{2}}^{L, M} (r_{1}, r_{2}) Y_{l_{1}, l_{2}}^{L, M} ({\hat{r}}_{1}, {\hat{r}}_{2}) . \end{matrix}

由于总波函数的内积定义为

\int \dots r_{1}^{2} d r_{1} d Ω_{1} r_{2}^{2} d r_{2} d Ω_{2}

，所以径向空间的内积定义为

\int \dots r_{1}^{2} d r_{1} r_{2}^{2} d r_{2}

。

　　由张量积空间中的结论，我们可以求哈密顿算符 $H$ 关于角向基底的 “矩阵元” $H_{λ, λ^{'}}$ ，每个矩阵元是径向空间中的一个算符。

\begin{matrix} (4) & H_{λ, λ^{'}} = ⟨ Y_{λ} | H | Y_{λ^{'}} ⟩ . \end{matrix}

列出薛定谔方程的 “矩阵形式”，就得到了一组耦合的二维径向波函数的薛定谔方程

\begin{matrix} (5) & \sum_{λ^{'}} H_{λ, λ^{'}} | R_{λ^{'}} ⟩ = i \frac{\partial}{\partial t} | R_{λ} ⟩, \end{matrix}

总哈密顿可以表示为

\begin{matrix} (6) & H = H_{1} + H_{2} + V_{12} + V_{F 1} + V_{F 2} . \end{matrix}

其中

H_{i} (i = 1, 2)

是单个电子的哈密顿算符（式 11 ），

V_{12}

是两电子之间的库仑势能，

V_{F i}

是电场对每个电子的作用势能。

　　 $H_{i}$ 不耦合分波，对应对角矩阵

\begin{matrix} (7) & \begin{aligned} ⟨ Y_{λ} | H_{i} | Y_{λ^{'}} ⟩ & = δ_{λ, λ^{'}} (K_{r i} + \frac{L_{i}^{2}}{2 r_{i}^{2}} - \frac{2}{r_{i}}) \\ = δ_{λ, λ^{'}} (- \frac{1}{2 m} \frac{\partial^{2}}{\partial {r_{i}}^{2}} + \frac{l_{i}^{2}}{2 m r_{i}^{2}} - \frac{2}{r_{i}}) (i = 1, 2), \end{aligned} \end{matrix}

其中第二项

L_{i}

变为

l_{i}

是因为

| Y_{λ} ⟩

基底是

L_{i}^{2}

的本征函数。剩下的哈密顿项

V_{12} + V_{F 1} + V_{F 2}

都会耦合分波。

2. 波函数的对称性

　　我们一般假设电子自旋态恒为 singlet（反对称），所以总波函数满足粒子交换对称 $Ψ (r_{1}, r_{2}) = Ψ (r_{2}, r_{1})$ 。由式 7 可以导出分波的对称性

\begin{matrix} (8) & ψ_{l_{1}, l_{2}}^{L, M} (r_{1}, r_{2}) = (- 1)^{l_{1} + l_{2} - L} ψ_{l_{2}, l_{1}}^{L, M} (r_{2}, r_{1}) . \end{matrix}

理论上用该式可以在程序中减少一半重复的分波，并且分波的 coupling 演化也可以得到精简，但由于编程麻烦暂时没有实现。

　　另外可以证明（其实是数值计算发现的） $l_{1} + l_{2} - L$ 为奇数的分波（奇分波）和 $l_{1} + l_{2} - L$ 为偶数的分波（偶分波）在线偏振电场中是独立演化的，也就是 $V_{12}$ 和 $z_{1}, z_{2}$ 不会把奇偶性不同的分波耦合起来。所以如果氦原子从基态（只包含偶分波： $l_{1} = l_{2}, L = 0$ ）开始在线偏振电场中演化，那么奇数分波的项将始终为零，可以在程序中去除。

3. 电子相互作用项

\begin{matrix} (9) & \begin{aligned} V_{12} = \frac{1}{| r_{2} - r_{1} |} & = 4 π \sum_{l = 0}^{\infty} \frac{1}{2 l + 1} \frac{r_{<}^{l}}{r_{>}^{l + 1}} \sum_{m = - l}^{l} Y_{l, m}^{*} ({\hat{r}}_{1}) Y_{l, m} ({\hat{r}}_{2}) \\ = 4 π \sum_{l = 0}^{\infty} \frac{(- 1)^{l}}{\sqrt{2 l + 1}} \frac{r_{<}^{l}}{r_{>}^{l + 1}} Y_{l, l}^{0, 0} ({\hat{r}}_{1}, {\hat{r}}_{2}) . \end{aligned} \end{matrix}

这就相当于将张量积空间中的线性算符分解成径向和角向算符的张量积之和。第二步使用了式 9 ，即

\begin{matrix} (10) & Y_{l, l}^{0, 0} ({\hat{r}}_{1}, {\hat{r}}_{2}) = \frac{(- 1)^{l}}{\sqrt{2 l + 1}} \sum_{m = - l}^{l} Y_{l m}^{*} ({\hat{r}}_{1}) Y_{l m} ({\hat{r}}_{2}) . \end{matrix}

　　要计算矩阵元 $⟨ Y_{λ} | V_{12} | Y_{λ^{'}} ⟩$ ，就要对 6 个球谐函数的乘积的线性组合做两次角向积分。使用式 12 可以将上式表示为六个 CG 系数相乘的线性组合（二重求和）。

\begin{matrix} (11) & \begin{aligned} ⟨ Y_{l_{1} l_{2}}^{L M} | Y_{l m}^{*} ({\hat{r}}_{1}) Y_{l m} ({\hat{r}}_{2}) | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'} M^{'}} ⟩ \\ = \sum_{m_{1}^{'}, m_{2}^{'}} \sum_{m_{1}, m_{2}} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2}^{'} & L^{'} \\ m_{1}^{'} & m_{2}^{'} & M^{'} \end{array}] \times \\ \iint Y_{l_{1} m_{1}}^{*} ({\hat{r}}_{1}) Y_{l_{2} m_{2}}^{*} ({\hat{r}}_{2}) Y_{l m}^{*} ({\hat{r}}_{1}) Y_{l m} ({\hat{r}}_{2}) Y_{l_{1}^{'} m_{1}^{'}} ({\hat{r}}_{1}) Y_{l_{2}^{'} m_{2}^{'}} ({\hat{r}}_{2}) d Ω_{1} d Ω_{2} \\ = \sum_{m_{1}^{'}, m_{2}^{'}} \sum_{m_{1}, m_{2}} (- 1)^{m_{1} + m_{2} + m} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2}^{'} & L^{'} \\ m_{1}^{'} & m_{2}^{'} & M^{'} \end{array}] \times \\ \int Y_{l_{1}, - m_{1}} ({\hat{r}}_{1}) Y_{l, - m} ({\hat{r}}_{1}) Y_{l_{1}^{'} m_{1}^{'}} ({\hat{r}}_{1}) d Ω_{1} \int Y_{l_{2}, - m_{2}} ({\hat{r}}_{2}) Y_{l m} ({\hat{r}}_{2}) Y_{l_{2}^{'} m_{2}^{'}} ({\hat{r}}_{2}) d Ω_{2} \\ = \frac{2 l + 1}{4 π} \sqrt{(2 l_{1} + 1) (2 l_{1}^{'} + 1) (2 l_{2} + 1) (2 l_{2}^{'} + 1)} \sum_{m_{1}^{'}, m_{2}^{'}} \sum_{m_{1}, m_{2}} (- 1)^{m_{1} + m_{2} + m} \times \\ (\begin{array}{c} l_{1} & l & l_{1}^{'} \\ 0 & 0 & 0 \end{array}) (\begin{array}{c} l_{1} & l & l_{1}^{'} \\ - m_{1} & - m & m_{1}^{'} \end{array}) (\begin{array}{c} l_{2} & l & l_{2}^{'} \\ 0 & 0 & 0 \end{array}) (\begin{array}{c} l_{2} & l & l_{2}^{'} \\ - m_{2} & m & m_{2}^{'} \end{array}) \times \\ [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2}^{'} & L^{'} \\ m_{1}^{'} & m_{2}^{'} & M^{'} \end{array}] . \end{aligned} \end{matrix}

现在试图对

m

求和并使用选择定则（3j 符号第二行之和为 0），得（注意

m

的范围）该求和中最多只有一项不为 0，所以

\begin{matrix} (12) & \begin{aligned} ⟨ Y_{l_{1} l_{2}}^{L M} | Y_{l, l}^{0, 0} | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'} M^{'}} ⟩ = \\ δ_{M, M^{'}} (- 1)^{l} \frac{\sqrt{2 l + 1}}{4 π} \sqrt{(2 l_{1} + 1) (2 l_{1}^{'} + 1) (2 l_{2} + 1) (2 l_{2}^{'} + 1)} \times \\ \sum_{m_{1}^{'}, m_{2}^{'}} \sum_{m_{1}, m_{2}} (- 1)^{m_{1}^{'} + m_{2}} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2}^{'} & L^{'} \\ m_{1}^{'} & m_{2}^{'} & M \end{array}] (\begin{array}{c} l_{1} & l & l_{1}^{'} \\ 0 & 0 & 0 \end{array}) \times \\ (\begin{array}{c} l_{1} & l & l_{1}^{'} \\ - m_{1} & m_{1} - m_{1}^{'} & m_{1}^{'} \end{array}) (\begin{array}{c} l_{2} & l & l_{2}^{'} \\ 0 & 0 & 0 \end{array}) (\begin{array}{c} l_{2} & l & l_{2}^{'} \\ - m_{2} & m_{2} - m_{2}^{'} & m_{2}^{'} \end{array}) . \end{aligned} \end{matrix}

其中对

m_{1}, m_{2}

的求和要求

\begin{matrix} (13) & m_{1} + m_{2} = m_{1}^{'} + m_{2}^{'} = M, | m_{1}^{'} - m_{1} | ⩽ l, | m_{2}^{'} - m_{2} | ⩽ l . \end{matrix}

　　由于 CG 系数都是实数，这必定是一个实数矩阵。选择定则如下

根据总角动量守恒（ $1 / r_{12}$ 算符与 $L, L_{z}$ 算符对易）， $L \neq L^{'}$ 或 $M \neq M^{'}$ 时，矩阵元为零。
根据 parity CG coefficients，当 $l_{1}^{'} + l + l_{1}$ 或 $l_{2}^{'} + l + l_{2}$ 为奇数时，上式等于 0。
根据 $Π Y = (- 1)^{l_{1} + l_{2}} Y$ （式 5 ），考虑到 $1 / r_{12}$ 具有偶宇称，所以 $l_{1} + l_{2}$ 与 $l_{1}^{'} + l_{2}^{'}$ 的奇偶必须不同。

　　爱华的论文中将式 12 用 9j 符号表示，但仅限于 $M \neq M^{'}$ 。然而经过数值验证，我发现应该可以将爱华的公式拓展为

\begin{matrix} (14) & \begin{aligned} ⟨ Y_{l_{1} l_{2}}^{L M} | Y_{l l}^{00} | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'} M^{'}} ⟩ = & \frac{2 l + 1}{4 π} δ_{L, L^{'}} δ_{M, M^{'}} \sqrt{(2 l_{1}^{'} + 1) (2 l_{2}^{'} + 1) (2 L + 1)} \times \\ [\begin{array}{c} l & l_{1}^{'} & l_{1} \\ 0 & 0 & 0 \end{array}] [\begin{array}{c} l & l_{2}^{'} & l_{2} \\ 0 & 0 & 0 \end{array}] {\begin{array}{c} l & l_{1}^{'} & l_{1} \\ l & l_{2}^{'} & l_{2} \\ 0 & L & L \end{array}} . \end{aligned} \end{matrix}

注意当

M = M^{'}

时，结果与

M

无关。

泊松积分

　　按照 FEDVR 基底的思路，我们会自然地想把 $V_{12}$ 算符展开后的 $⟨ r_{i} r_{j} | r_{<}^{l} / r_{>}^{l} | r_{i^{'}} r_{j^{'}} ⟩$ 用高斯 Lobatto 积分来计算，然而这么做并不精确，因为 $r_{<}^{l} / r_{>}^{l}$ 用有限阶多项式展开会有误差。使用泊松积分法可以减小计算误差，且仍然保持对角矩阵的形式，即

\begin{matrix} (15) & ⟨ r_{i} r_{j} | \frac{r_{<}^{l}}{r_{>}^{l + 1}} | r_{i^{'}} r_{j^{'}} ⟩ \propto δ_{i, i^{'}} δ_{j, j^{'}} . \end{matrix}

根据我的猜测（有空验证一下！），泊松积分积分的结果应该和直接用数值积分的结果是一样的。

\begin{matrix} (16) & ⟨ r_{i} r_{j} | \frac{r_{<}^{l}}{r_{>}^{l + 1}} | r_{i^{'}} r_{j^{'}} ⟩ = δ_{i, i^{'}} δ_{j, j^{'}} [\frac{2 l + 1}{r_{i} r_{j} \sqrt{ω_{i} ω_{j}}} (2 T_{l})_{i, j}^{- 1} + \frac{r_{i}^{l} r_{j}^{l}}{r_{m a x}^{2 l + 1}}] . \end{matrix}

推导参考 McCurdy, Solving the three-body Coulomb breakup problem using exterior complex scaling 式 68。其中

T_{l}

是单电子动能算符的矩阵

\begin{matrix} (17) & \begin{aligned} (T_{l})_{i j} & = ⟨ r_{i} | [- \frac{1}{2 m} \frac{d^{2}}{d r^{2}} + \frac{l (l + 1)}{2 m r}] | r_{j} ⟩ \\ = - \frac{1}{2 m} ⟨ r_{i} | \frac{d^{2}}{d r^{2}} | r_{j} ⟩ + δ_{i, j} \frac{l (l + 1)}{2 m r_{i}^{2}} . \end{aligned} \end{matrix}

其中

| r_{i} ⟩

是一维 FEDVR 格点在

r_{i}

处的正交归一基底，

r_{m a x}

是计算

T_{l}

时最后一个 FE 的边界。虽然式 16 中含有

r_{m a x}

，但结果却与

r_{m a x}

无关，原因是

T_{l}

也和

r_{m a x}

4. 电场作用项（长度规范）

　　长度规范中，对每个电子，

\begin{matrix} (18) & V_{F} = E \cdot r = E_{x} x + E_{y} y + E_{z} z \end{matrix}

与氢原子的情况相同，有

\begin{matrix} (19) & x = \sqrt{\frac{2 π}{3}} r (Y_{1, - 1} - Y_{1, 1}), y = i \sqrt{\frac{2 π}{3}} r (Y_{1, - 1} + Y_{1, 1}), z = 2 \sqrt{\frac{π}{3}} r Y_{1, 0} . \end{matrix}

对线偏振电场我们只需要最后一项，以第一个电子为例，令

\begin{matrix} (20) & F^{(z 1)} = \cos θ_{1} . \end{matrix}

\begin{matrix} (21) & \begin{aligned} ⟨ Y_{l_{1} l_{2}}^{L M} | \cos θ_{1} | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'} M^{'}} ⟩ = 2 \sqrt{\frac{π}{3}} \sum_{m_{1}^{'}, m_{2}^{'}} \sum_{m_{1}, m_{2}} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2} & L^{'} \\ m_{1}^{'} & m_{2}^{'} & M^{'} \end{array}] \times \\ \iint Y_{l_{1} m_{1}}^{*} ({\hat{r}}_{1}) Y_{l_{2} m_{2}}^{*} ({\hat{r}}_{2}) Y_{10} ({\hat{r}}_{1}) Y_{l_{1}^{'} m_{1}^{'}} ({\hat{r}}_{1}) Y_{l_{2}^{'} m_{2}^{'}} ({\hat{r}}_{2}) d Ω_{1} d Ω_{2} \\ = 2 \sqrt{\frac{π}{3}} δ_{l_{2}, l_{2}^{'}} \sum_{m_{1}, m_{2}, m_{1}^{'}} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2}^{'} & L^{'} \\ m_{1}^{'} & m_{2} & M^{'} \end{array}] \times \\ \int Y_{l_{1} m_{1}}^{*} ({\hat{r}}_{1}) Y_{10} ({\hat{r}}_{1}) Y_{l_{1}^{'} m_{1}^{'}} ({\hat{r}}_{1}) d Ω_{1} \\ = δ_{l_{2}, l_{2}^{'}} \sqrt{(2 l_{1} + 1) (2 l_{1}^{'} + 1)} \sum_{m_{1}, m_{2}, m_{1}^{'}} (- 1)^{m_{1}} \times \\ [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2} & L^{'} \\ m_{1}^{'} & m_{2} & M^{'} \end{array}] (\begin{array}{c} l_{1} & 1 & l_{1}^{'} \\ 0 & 0 & 0 \end{array}) (\begin{array}{c} l_{1} & 1 & l_{1}^{'} \\ - m_{1} & 0 & m_{1}^{'} \end{array}) \\ = δ_{l_{2}, l_{2}^{'}} δ_{M, M^{'}} \sqrt{(2 l_{1} + 1) (2 l_{1}^{'} + 1)} \sum_{m_{1}, m_{2}} (- 1)^{m_{1}} \times \\ [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2} & L^{'} \\ m_{1} & m_{2} & M \end{array}] (\begin{array}{c} l_{1} & 1 & l_{1}^{'} \\ 0 & 0 & 0 \end{array}) (\begin{array}{c} l_{1} & 1 & l_{1}^{'} \\ - m_{1} & 0 & m_{1} \end{array}) . \end{aligned} \end{matrix}

　　最后一步使用了 3j 符号中 $m_{1} + m_{2} + m_{3} = 0$ ，以及 CG 系数中 $m_{1} + m_{2} = M$ 的性质。两个 delta 函数验证了对第一个电子作用的 $z$ 方向电场不会影响第二个电子的角动量以及总角动量的 $z$ 分量。推导中还陆续得出了 $m_{1}^{'} = m_{1}, m_{2}^{'} = m_{2}$ 的结论，即该电场同样不会影响每个电子的角动量 $z$ 分量（所以对 $m_{1}^{'}, m_{2}^{'}$ 的求和消去了）。最后对 $m_{1}, m_{2}$ 的求和中，要求 $m_{1} + m_{2} = M$ ，且 $| m_{1} | < min {l_{1}, l_{1}^{'}}$ 。

　　同理，对第二个电子有

\begin{matrix} (22) & \begin{aligned} ⟨ Y_{l_{1} l_{2}}^{L M} | z_{2} | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'} M^{'}} ⟩ = δ_{l_{1}, l_{1}^{'}} δ_{M, M^{'}} \sqrt{(2 l_{2} + 1) (2 l_{2}^{'} + 1)} r \sum_{m_{1}, m_{2}} (- 1)^{m_{2}} \times \\ [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1} & l_{2}^{'} & L^{'} \\ m_{1} & m_{2} & M \end{array}] (\begin{array}{c} l_{2} & 1 & l_{2}^{'} \\ 0 & 0 & 0 \end{array}) (\begin{array}{c} l_{2} & 1 & l_{2}^{'} \\ - m_{2} & 0 & m_{2} \end{array}) . \end{aligned} \end{matrix}

　　在爱华的毕业论文中， $M = M^{'} = 0$ 时用 9j 符号表示为

\begin{matrix} (23) & \begin{aligned} ⟨ Y_{l_{1} l_{2}}^{L M} | z_{i} | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'} M^{'}} ⟩ = r \sqrt{9 (2 l_{1}^{'} + 1) (2 l_{2}^{'} + 1) (2 L^{'} + 1) / (4 π)^{2}} \\ \times [\begin{array}{c} δ_{i, 1} & l_{1}^{'} & l_{1} \\ 0 & 0 & 0 \end{array}] [\begin{array}{c} δ_{i, 2} & l_{2}^{'} & l_{2} \\ 0 & 0 & 0 \end{array}] [\begin{array}{c} 1 & L^{'} & L \\ 0 & 0 & 0 \end{array}] {\begin{array}{c} δ_{i, 1} & l_{1}^{'} & l_{1} \\ δ_{i, 2} & l_{2}^{'} & l_{2} \\ 1 & L^{'} & L \end{array}} (i = 1, 2), \end{aligned} \end{matrix}

选择定则：

L^{'} - L = \pm 1

，

M^{'} = M

，

l_{1} + l_{2} - L

奇偶性不变。这就是为什么从基态（

l_{1} = l_{2}

，

L = 0

）的电离计算可以排除所有

l_{1} + l_{2} - L

为奇数的分波。

　　但由于单光子只有 $l = 1$ ，所以 $l_{1} + l_{2} - L$ 奇偶性不变的条件还可以进一步变为 $l_{1}, l_{2}$ 其中一个改变 $\pm 1$ 。

5. 电场作用项（速度规范）

　　 特别注意：在速度规范下即使只考虑从基态的单电离，也需要好几个 $L$ ，因为电矢势不为零时，波函数比起长度规范叠乘了一个平面波，而这个平面波需要更多分波才能展开。

　　类比氢原子（式 25 ），每两个分波之间的耦合从一个数变为一个算符

\begin{matrix} (24) & F_{λ, λ^{'}}^{(v 1)} = F_{λ, λ^{'}}^{(z 1)} \frac{\partial}{\partial r_{1}} + \frac{F_{λ, λ^{'}}^{(v z 1)}}{r_{1}} . \end{matrix}

其中

F_{λ, λ^{'}}^{(z 1)}

在式 20 中定义。第二项

\begin{matrix} (25) & F^{(v z 1)} = - \cos θ_{1} - \sin θ_{1} \frac{\partial}{\partial θ_{1}} . \end{matrix}

为了方便暂且假设所有

M = 0

，有

\begin{matrix} (26) & \begin{aligned} F_{λ, λ^{'}}^{(v z 1)} & = ⟨ Y_{l_{1} l_{2}}^{L} | F^{(v z 1)} | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'}} ⟩ \\ = δ_{l_{2}, l_{2}^{'}} \sum_{m_{1}, m_{2}, m_{1}^{'}} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & 0 \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2}^{'} & L^{'} \\ m_{1}^{'} & m_{2} & 0 \end{array}] \times \\ \int Y_{l_{1} m_{1}}^{*} ({\hat{r}}_{1}) F^{(v z 1)} ({\hat{r}}_{1}) Y_{l_{1}^{'} m_{1}^{'}} ({\hat{r}}_{1}) d Ω_{1} \\ = δ_{l_{2}, l_{2}^{'}} \sum_{m_{1}} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & - m_{1} & 0 \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2}^{'} & L^{'} \\ m_{1} & - m_{1} & 0 \end{array}] \times \\ (δ_{l_{1}^{'}, l_{1} + 1} l_{1}^{'} C_{l_{1}, m_{1}} - δ_{l_{1}, l_{1}^{'} + 1} l_{1} C_{l_{1}^{'}, m_{1}}) . \end{aligned} \end{matrix}

积分

C_{l, m}

可以参考式 18 。同理，

\begin{matrix} (27) & \begin{aligned} F_{λ, λ^{'}}^{(v z 2)} & = ⟨ Y_{l_{1} l_{2}}^{L} | F^{(v z 2)} | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'}} ⟩ \\ = δ_{l_{1}, l_{1}^{'}} \sum_{m_{1}, m_{2}, m_{2}^{'}} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & 0 \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2}^{'} & L^{'} \\ m_{1} & m_{2}^{'} & 0 \end{array}] \times \\ \int Y_{l_{2} m_{2}}^{*} ({\hat{r}}_{2}) F^{(v z 2)} ({\hat{r}}_{2}) Y_{l_{2}^{'} m_{2}^{'}} ({\hat{r}}_{2}) d Ω_{1} \\ = δ_{l_{1}, l_{1}^{'}} \sum_{m_{2}} [\begin{array}{c} l_{1} & l_{2} & L \\ - m_{2} & m_{2} & 0 \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2}^{'} & L^{'} \\ - m_{2} & m_{2} & 0 \end{array}] \times \\ (δ_{l_{2}^{'}, l_{2} + 1} l_{2}^{'} C_{l_{2}, m_{2}} - δ_{l_{2}, l_{2}^{'} + 1} l_{2} C_{l_{2}^{'}, m_{2}}) . \end{aligned} \end{matrix}

　　 选择定则： 经过数值验证，速度规范的选择定则同样可以保证 $l_{1} + l_{2} - L$ 奇偶性不变。

　　 对称性： 经过数值验证， $F_{(l_{1}, l_{2}, L), (l_{1}^{'}, l_{2}^{'}, L^{'})}^{(v z 1)} = F_{(l_{2}, l_{1}, L), (l_{2}^{'}, l_{1}^{'}, L^{'})}^{(v z 2)}$ 。

6. 非线性偏振电场

　　对非线性偏振电场，式 18 的前两项不为零，但只和 $z$ 分量的结果大同小异（只有最后一个 3j 系数变为两项，再除以 $\sqrt{2}$ 以归一化）

\begin{matrix} (28) & \begin{aligned} ⟨ Y_{l_{1} l_{2}}^{L M} | x_{1} | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'} M^{'}} ⟩ = \frac{δ_{l_{2}, l_{2}^{'}} δ_{M, M^{'}}}{\sqrt{2}} \sqrt{(2 l_{1} + 1) (2 l_{1}^{'} + 1)} r \times \\ \sum_{m_{1}, m_{2}} (- 1)^{m_{1}} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2} & L^{'} \\ m_{1} & m_{2} & M \end{array}] \times \\ (\begin{array}{c} l_{1} & 1 & l_{1}^{'} \\ 0 & 0 & 0 \end{array}) [(\begin{array}{c} l_{1} & 1 & l_{1}^{'} \\ - m_{1} & - 1 & m_{1} \end{array}) - (\begin{array}{c} l_{1} & 1 & l_{1}^{'} \\ - m_{1} & 1 & m_{1} \end{array})] . \end{aligned} \end{matrix}

\begin{matrix} (29) & \begin{aligned} ⟨ Y_{l_{1} l_{2}}^{L M} | y_{1} | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'} M^{'}} ⟩ = \frac{i δ_{l_{2}, l_{2}^{'}} δ_{M, M^{'}}}{\sqrt{2}} \sqrt{(2 l_{1} + 1) (2 l_{1}^{'} + 1)} r \times \\ \sum_{m_{1}, m_{2}} (- 1)^{m_{1}} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1}^{'} & l_{2} & L^{'} \\ m_{1} & m_{2} & M \end{array}] \times \\ (\begin{array}{c} l_{1} & 1 & l_{1}^{'} \\ 0 & 0 & 0 \end{array}) [(\begin{array}{c} l_{1} & 1 & l_{1}^{'} \\ - m_{1} & - 1 & m_{1} \end{array}) + (\begin{array}{c} l_{1} & 1 & l_{1}^{'} \\ - m_{1} & 1 & m_{1} \end{array})] . \end{aligned} \end{matrix}

\begin{matrix} (30) & \begin{aligned} ⟨ Y_{l_{1} l_{2}}^{L M} | x_{2} | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'} M^{'}} ⟩ = \frac{δ_{l_{1}, l_{1}^{'}} δ_{M, M^{'}}}{\sqrt{2}} \sqrt{(2 l_{2} + 1) (2 l_{2}^{'} + 1)} r \\ \sum_{m_{1}, m_{2}} (- 1)^{m_{2}} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1} & l_{2}^{'} & L^{'} \\ m_{1} & m_{2} & M \end{array}] \times \\ (\begin{array}{c} l_{2} & 1 & l_{2}^{'} \\ 0 & 0 & 0 \end{array}) [(\begin{array}{c} l_{2} & 1 & l_{2}^{'} \\ - m_{2} & - 1 & m_{2} \end{array}) - (\begin{array}{c} l_{2} & 1 & l_{2}^{'} \\ - m_{2} & 0 & m_{1} \end{array})] . \end{aligned} \end{matrix}

\begin{matrix} (31) & \begin{aligned} ⟨ Y_{l_{1} l_{2}}^{L M} | y_{2} | Y_{l_{1}^{'} l_{2}^{'}}^{L^{'} M^{'}} ⟩ = \frac{i δ_{l_{1}, l_{1}^{'}} δ_{M, M^{'}}}{\sqrt{2}} \sqrt{(2 l_{2} + 1) (2 l_{2}^{'} + 1)} r \\ \sum_{m_{1}, m_{2}} (- 1)^{m_{2}} [\begin{array}{c} l_{1} & l_{2} & L \\ m_{1} & m_{2} & M \end{array}] [\begin{array}{c} l_{1} & l_{2}^{'} & L^{'} \\ m_{1} & m_{2} & M \end{array}] \times \\ (\begin{array}{c} l_{2} & 1 & l_{2}^{'} \\ 0 & 0 & 0 \end{array}) [(\begin{array}{c} l_{2} & 1 & l_{2}^{'} \\ - m_{2} & - 1 & m_{2} \end{array}) + (\begin{array}{c} l_{2} & 1 & l_{2}^{'} \\ - m_{2} & 0 & m_{1} \end{array})] . \end{aligned} \end{matrix}

7. 束缚态

　　能量较低的束缚态可以轻易用虚时间演化得到，即把 $\exp (- i H Δ t)$ 替换为 $\exp (- H Δ t)$ ，这相当于把 $Δ t$ 变为虚数 $- i Δ t$ ，因此得名。氦原子基态只包含 $L = 0$ 的分波，这要求 $l_{1} = l_{2} = 0, 1, 2, \dots$ （参考图 2 ）。

　　注意氦原子基态只需要由 $L = 0$ 的分波展开。另外要特别注意，千万不要对束缚态的分波进行截断，这样会产生类似冲击波的噪音，其强度可以媲美双电离。

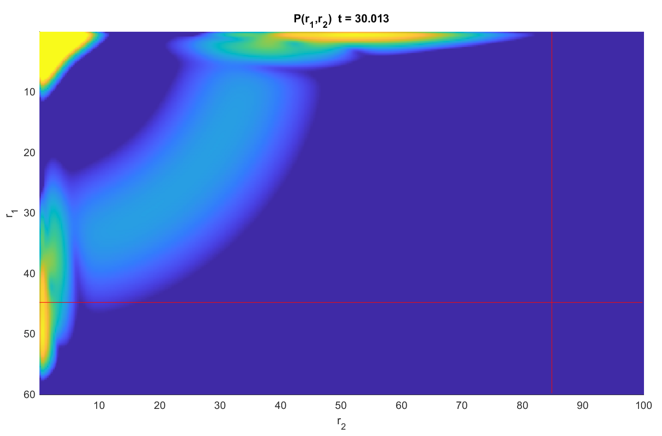
图 1：束缚态分波截断噪音（氦原子单电离 110eV，速度规范整体 Lanczos 算法）

图 2：束缚态分波截断噪音 2（缩小时间步长，增加 Krylov 阶数）

图 3：完美波形（Lanczos 算法 11eV 单电离。Krylov 阶数 15，时间步长 0.025，Locatto 节点数 6，等间距 FE 1 au，分波配置 3,3,3）

8. Crank-Nicolson 波函数演化

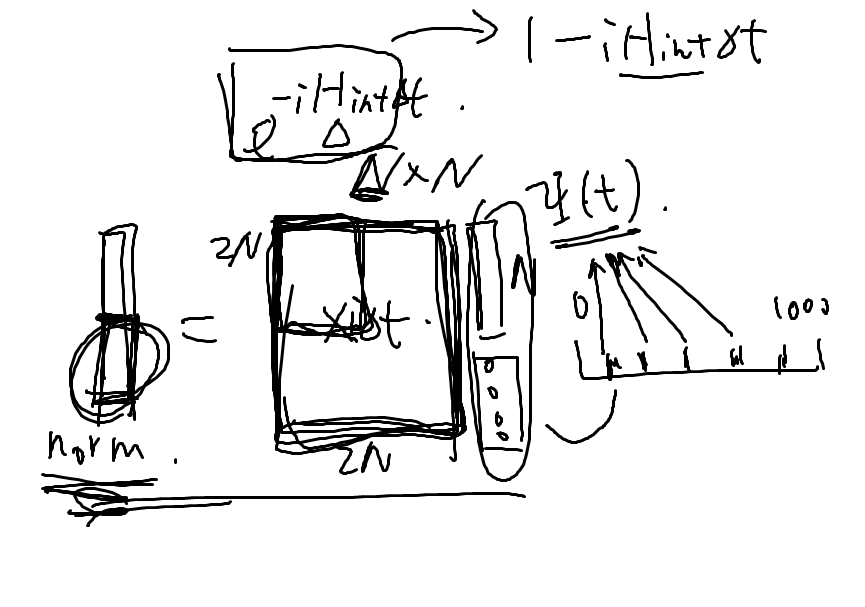
　　对薛定谔方程式 5 做 Crank-Nicolson 演化（propagation）同样使用 split operator

\begin{matrix} (32) & \exp (- i H Δ t) = \exp (- i H_{0} \frac{Δ t}{2}) \exp (- i H_{i n t} Δ t) \exp (- i H_{0} \frac{Δ t}{2}) + O (Δ t^{3}) . \end{matrix}

只是这里的

H_{i n t} = V_{12} + V_{F}

是所有

⟨ Y | | Y ⟩

作用后为非对角（算符）矩阵的项，即电子的相互作用和电场对每个电子的作用。

　　 $H_{0} = H_{1} + H_{2}$ 由于 $H_{1}$ 和 $H_{2}$ 对易，我们可以将它们独立演化而不产生误差（式 3 ）：

\begin{matrix} (33) & \exp (- i H_{0} \frac{Δ t}{2}) = \exp (- i H_{1} \frac{Δ t}{2}) \exp (- i H_{2} \frac{Δ t}{2}) . \end{matrix}

也就是对每个 partial wave 的二维网格，用类似氢原子的方法演化每一列再演化每一行。

　　根据以上的推导可以看出 $H_{i n t}$ 在展开成径向算符与角向算符的张量积的线性组合后，径向算符都是关于 $r$ 的函数，这对 FEDVR 基底来说都是对角矩阵（即使使用泊松积分）。所以在演化 $\exp (- i H_{i n t} Δ t)$ 时，每个二维 FEDVR 格点都可以独立进行，给大量并行提供了可能性。总结起来，程序中的三维波函数矩阵的每个方向的演化都可以每列独立进行。

　　在演化 $\exp (- i H_{i n t} Δ t)$ 的时候，爱华的做法是进一步 split 成三个 operators

\begin{matrix} (34) & \exp (- i H_{i n t} Δ t) = \exp (- i V_{F} \frac{Δ t}{2}) \exp (- i V_{12} Δ t) \exp (- i V_{F} \frac{Δ t}{2}) . \end{matrix}

这是因为

V_{F} = V_{F 1} + V_{F 2}

是含时的，和电场分量

E_{z}

成正比。

　　爱华进一步分割的原因是，他的代码中预先储存了 $V_{F}$ 和 $V_{12}$ 对角化后的本征值和本征矢矩阵，如果直接对 $H_{i n t}$ 对角化，那么就需要每一步都重新对角化一次。预先储存所需的内存和分波数的平方成正比，然而当我们需要很多分波的时候，内存就远远不够了。为了解决内存问题，我径向和角向都使用 Crank-Nicolson 演化，而且每个时间步长对每个格点重新生成 $V_{F} + V_{12}$ 矩阵并一次演化不需要分成三次。对于波函数绝对值低于某个阈值的格点，我们甚至可以忽略不演化。

　　另外一点，如果只关心 single ionization，可以用一个长方形网格（见 Ossiander 2017 Nat. Phys.）。但要注意在短边加入 absorber 防止反射。）

9. Lanczos 波函数演化

　　 Lanczos 算法是 Pazourek 组用的。注意他们并没有使用算符拆分。一口气把整个哈密顿作用在波函数上。它们使用等间距 FE，Krylov 基底的数量在 15 左右。通过调整时间步长来固定误差估计。

10. 分波收敛分析

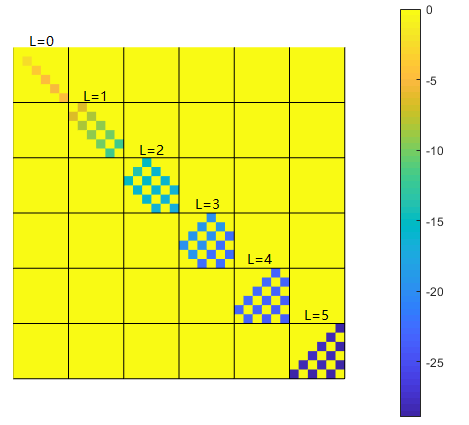
　　使用 $l_{1, m a x}, l_{2, m a x}, L_{m a x}$ 来生成分波列表有时候会有较大的浪费，会出现许多概率极小的分波。最好的办法是把各个分波的概率画成图，从图中可以轻易看出分波是否收敛以及是否有浪费。

图 4：

l_{1, m a x}, l_{2, m a x}, L_{m a x} = 5

，可以看出

L

较小时需要更大

l_{1}, l_{2}

，而

L

较大时浪费严重。理想情况是每个

L

中最小概率的分波都差不多。

11. 时间步长误差分析以及变步长演化

　　首先要注意的是一个电磁场周期至少要有若干个步长，可以在程序中检查。

　　对于任何演化算法，一个最简单的方法就是每隔一段时间，使用 dt/N（ $N = 2$ 或 $4$ ）为步长，演化 $N$ 次然后和 dt 一次的结果做对比，计算 $‖ Δ Ψ^{'} - Δ Ψ ‖ / ‖ Δ Ψ ‖$ 用于衡量相对误差。其中 $Δ Ψ = Ψ (t + d t) - Ψ (t)$ 。然而这对 Crank-Nicolson 似乎不准。

　　对于 Lanzos，有标准的误差公式，也可以和 $‖ Δ Ψ^{'} - Δ Ψ ‖ / ‖ Δ Ψ ‖$ 对比看看哪个更准。

12. 分波误差分析（原创）

　　我们截取有限个分波时，在分波演化（式 34 ）的过程中，会引入新的误差。截取以后， $V_{F}, V_{12}$ 仍然是厄米矩阵，所以他们的传播子同样是幺正的，所以不能用波函数的模长来估计误差。所以可以用另一种方法来估计误差。误差可以每隔几步估算一次，令 $V_{F}^{'}, V_{12}^{'}$ 为两倍基底数量的矩阵，那么可以计算 $(i V_{F}^{'} Δ t) v$ 比基底多出来的几个分波，对每个分波的绝对值进行求和。

图 5：分波误差分析

13. 束缚态

　　理论上可以数值解总哈密顿矩阵的本征值，但实际上这个矩阵大到几乎不可能解出（事实上我们从来不会把总哈密顿矩阵直接储存，而是储存 split operator）。我们使用虚时间演化（imaginary time propagation）。

　　虚时演化的初始态我用的是两个 He+ 的基态相乘（实数波函数），和爱华略有不同，不过这影响不大。由于我们的 split operator 都是实数矩阵，使用虚时间后其指数函数也是实数矩阵，所以虚时间演化得到的基态波函数也一定会是纯实数。我们只需用 $L = 0, M = 0$ 的所有 partial waves 即可。

14. 双电子近似

　　 Argon 的电子数为 $N = 18$ ，基态电离势能为 $I_{p} = 15.6 eV$ （ $0.5733 au$ ），使用等效势能

\begin{matrix} (35) & V_{e f f} = \frac{- 2 - (N - 2) e^{- r / a}}{r} + V_{0} e^{- r / b}, \end{matrix}

满足

V_{e f f} (r \to \infty) \to - 2 / r

，当

V_{e f f} (r \to 0) \to - N / r

。参数

a

越小屏蔽势能的半径就越小，越接近于氦原子，电离势能越大。

15. Streaking 的分波数

　　 Pazourek 组同时实现了长度和速度规范。[Pazo12] 的 TDSE solver 主要参考是 [Feis08]，这篇讨论的是 sequential 双电离，cross section 使用了最多 $L_{m a x}, l_{1, m a x}, l_{2, m a x}$ 最大 $(4, 9, 9)$ ，且长度规范和速度规范一致。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。