类氢原子斯塔克效应（微扰）

贡献者： addis

本文存在未完成的内容。

预备知识　不含时微扰理论，含连续态的不含时微扰理论（量子力学），氢原子的跃迁偶极子矩阵元计算（束缚态之间）

　　微扰理论（ $E_{z}$ 是 $z$ 方向电场）：

\begin{matrix} (1) & H^{'} = E_{z} z . \end{matrix}

矩阵元为

\begin{matrix} (2) & H_{l^{'}, l}^{'} = E_{z} ⟨ ψ_{n, l^{'}, m} | z | ψ_{n, l, m} ⟩ . \end{matrix}

　　但事实上氢原子加上匀强电场后是不存在数学上严格的束缚态的，因为无论电场多弱，在电场反方向的某个距离外，势能都会小于基态能量，使波函数变为散射态。在含时薛定谔方程中，波函数可能会有长时间处于微扰理论给出的 “束缚态”，但这只能算是一种亚稳态（metastable state），仍会有不为零的隧道电离概率。

例 1　类氢原子 $n = 2$ 的斯塔克效应

　　先考虑 $n = 2$ ， $m = 0$ 的情况，这是一个二维希尔伯特子空间，基底为 $| 2, 0, 0 ⟩$ 和 $| 2, 1, 0 ⟩$ 。根据表 1 ，式 2 为

\begin{matrix} (3) & H^{'} = - \frac{3}{Z} E_{z} (\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}) . \end{matrix}

本征值为

E_{\pm}^{1} = \mp \frac{3}{Z} E_{z}

，好本征态为

| 2 \pm 0 ⟩ = (| 200 ⟩ \pm | 210 ⟩) / \sqrt{2}

，也被称为 Stark 态。

图 1：氢原子

| 2 + ⟩

的概率密度函数的

x

z

切面，可见电子向下偏移，电场向上为正，所以本征能量变小。

| 2 - ⟩

态是此图上下翻转，本征能量变大。

　　不要以为图 1 是外电场扭曲波函数的结果， $| 2 \pm ⟩$ 本身就是无电场的氢原子 $n = 2$ 本征态。施加了电场后波函数反而需要进一步修正。

　　从经典电磁学角度来理解，电偶极子在电场中的能量（式 7 ）等于 $- d_{z} E_{z}$ ，其中 $d_{z}$ 是 $z$ 方向电偶极子

\begin{matrix} (4) & d_{z}^{(\pm)} = ⟨ 2 \pm | z | 2 \pm ⟩ = \pm \frac{3}{Z} . \end{matrix}

所以 Stark 效应的一阶能量修正和电场成功正比，产生原因是恒定的 Stark 态在电场中的额外能量。一阶波函数修正其实不给一阶能量修正做贡献。

例 2　氢原子斯塔克效应（能级截断）

未完成：这不太可行！如果把

n_{max}

增加到 5-15，就会得到奇怪的结果（尤其是直接计算

⟨ ψ_{n} | H^{1} / E | ψ_{n} ⟩

，图 2 也会出现奇怪的 avoided crossing。这是因为，波函数被电场扭曲以后并不完全能够用束缚态展开，而是同时需要许多连续态！从数值方法上，我们可以规定给一个

r_{max}

把氢原子束缚到一个盒子中，用离散的

E > 0

盒子束缚态来近似连续态。所以还是先看例 3 吧。

事实上，在例 3 中使用式 9 计算二阶微扰十分繁琐，通常需要编程来数值计算。除了按不同阶来计算微扰外，还有一个更直接的近似方法就是直接把总哈密顿

H = H^{0} + H^{1}

用有限个

| n, l, m ⟩

（可以用

n_{max}

作为截断条件）完整表示（例如表 1 ），然后数值将其对角化。当

n_{max}

无穷大，结果就是精确的（包含任意阶微扰）。若使用编程，该算法将比例 3 更容易实现。

　　首先可以用 “氢原子的跃迁偶极子矩阵元列表” 中的 h_dipole_z.m 程序生成 $H^{1}$ 矩阵，然后用 Matlab 自带的 eigen() 函数求 $H^{0} + H^{1}$ 的本征值，画出每个能级关于电场强度的曲线。

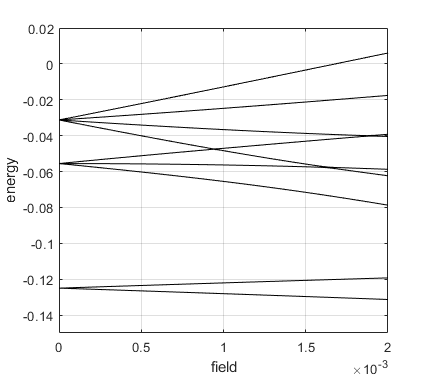
图 2：当电场（横坐标）增加时，氢原子

n = 2, 3, 4

的能级分裂（使用原子单位）

　　从这里我们肉眼只能看出 $E_{n}^{1}$ 随电场的线性变化，但曲线中包含了任意 $E_{n}^{m}$ 。

例 3　氢原子的极化率（二阶微扰）

　　在二阶微扰的式 1 中，类氢原子的 $E_{n}^{0} \propto Z^{2}$ ，分子中的跃迁矩阵元 $\propto 1 / Z$ ，所以二阶能量修正 $E_{n}^{2} \propto 1 / Z^{4}$ （参考 [1]）。

　　若氢原子处于某个好量子态，使用一阶微扰求其极化率（polarizability） $α$ ，这里定义为

\begin{matrix} (5) & p_{z} = α E_{z}, \end{matrix}

其中

p_{z}

为

z

方向的电偶极子，

E_{z}

为电场强度。如果系统不是关于

z

轴对称，极化率一般是一个

3 \times 3

张量（矩阵）。

　　该问题中， $H^{1} = E_{z} z$ ， $p_{z} = - ⟨ ψ_{n} | z | ψ_{n} ⟩$ （这里的 $n$ 只是一个一般编号，不代表主量子数）。使用波函数的一阶修正 $ψ_{n} \approx ψ_{n}^{0} + ψ_{n}^{1}$ ，有

\begin{matrix} (6) & \begin{aligned} p_{z} & \approx - ⟨ ψ_{n}^{0} + ψ_{n}^{1} | z | ψ_{n}^{0} + ψ_{n}^{1} ⟩ \\ = - ⟨ ψ_{n}^{0} | z | ψ_{n}^{0} ⟩ - 2 Re ⟨ ψ_{n}^{0} | z | ψ_{n}^{1} ⟩ - ⟨ ψ_{n}^{1} | z | ψ_{n}^{1} ⟩ . \end{aligned} \end{matrix}

其中第一项就是

- E_{n}^{1} / E_{z}

。第二项第三项分别是二阶和三阶小量，所以第三项可忽略。根据式 6 ，

⟨ ψ_{n}^{0} | z | ψ_{n}^{1} ⟩ = E_{n}^{2} / E_{z}

对应二阶能量修正，所以

\begin{matrix} (7) & p_{n, z} \approx p_{n, z}^{1} + p_{n, z}^{2} = - \frac{1}{E_{z}} (E_{n}^{1} + 2 E_{n}^{2}) . \end{matrix}

其中一阶能量修正

\begin{matrix} (8) & E_{n}^{1} = ⟨ ψ_{n}^{0} | H^{1} | ψ_{n}^{0} ⟩ \end{matrix}

和电场成正比和

Z

成反比，而二阶能量修正（式 1 ）

\begin{matrix} (9) & E_{n}^{2} = \sum_{m}^{E_{m} \neq E_{n}} \frac{{| ⟨ ψ_{m}^{0} | H^{1} | ψ_{n}^{0} ⟩ |}^{2}}{E_{n}^{0} - E_{m}^{0}} . \end{matrix}

正比于电场平方以及

1 / Z^{2}

。

　　可见 $p_{n, z}^{1}$ 是一个常数，而 $p_{n, z}^{2}$ 正比于电场，并决定极化率

\begin{matrix} (10) & α_{n} = - \frac{2 E_{n}^{2}}{E_{z}^{2}} . \end{matrix}

　　球面波基底为（式 9 ）

\begin{matrix} (11) & | C_{l, m} (k) ⟩ = \frac{1}{r} \sqrt{\frac{2}{π}} F_{l} (η, k r) Y_{l, m} (\hat{r}), \end{matrix}

式 2 在 Stark 效应中就是

\begin{matrix} (12) & E_{n}^{2} = \sum_{n^{'}, l^{'}}^{n^{'} \neq n} \frac{{| ⟨ n^{'}, l^{'}, m | H^{1} | n, α, m ⟩ |}^{2}}{E_{n}^{0} - E_{n^{'}}^{0}} + \sum_{l^{'}} \int_{0}^{\infty} \frac{{| ⟨ C_{l^{'}, m} (k) | H^{1} | n, α, m ⟩ |}^{2}}{E_{n}^{0} - k^{2} / 2} d k . \end{matrix}

其中

| n, α, m ⟩

不过是

| n, l, m ⟩

的线性组合。第一个矩阵元为（式 2 ）

\begin{matrix} (13) & \begin{aligned} ⟨ ψ_{n^{'}, l^{'}, m^{'}} | r \cos θ | ψ_{n, l, m} ⟩ \\ = δ_{m, m^{'}} (δ_{l + 1, l^{'}} C_{l, m} + δ_{l, l^{'} + 1} C_{l^{'}, m^{'}}) \int_{0}^{\infty} R_{n^{'}, l^{'}} (r) R_{n, l} (r) r^{3} d r . \end{aligned} \end{matrix}

而第二个也是大同小异（式 11 ），

\begin{matrix} (14) & \begin{aligned} ⟨ C_{l^{'}, m} (k) | r \cos θ | ψ_{n, l, m} ⟩ \\ = δ_{m, m^{'}} (δ_{l + 1, l^{'}} C_{l, m} + δ_{l, l^{'} + 1} C_{l^{'}, m^{'}}) \sqrt{\frac{2}{π}} \int_{0}^{\infty} F_{l} (η, k r) (\hat{r}) R_{n, l} (r) r^{2} d r . \end{aligned} \end{matrix}

　　对 $| 2, \pm, 0 ⟩$ ，由于选择定则 $Δ l = \pm 1$ ，绝对值内不会同时出现两项，所以 $E_{2, \pm, 0}^{2} = (E_{2, 0, 0}^{2} + E_{2, 1, 0}^{2}) / 2$ 。但 $n = 3$ 的时不可以这样。另外非简并的 $| 2, 1, \pm 1 ⟩$ 极化率同 $| 2, 1, 0 ⟩$ 。

1. 含时问题

　　以上我们讨论的都是不含时问题。但是在真正的斯塔克效应实验中，电场是随时间慢慢增加的。如果初始时，波函数处于 $n = 2$ 子空间的任意状态，例如 $| 210 ⟩$ ，那么当缓慢施加电场后，波函数会如何变化？这可以参考 “绝热近似（量子力学）”。

例 4　 $| n, l, m ⟩$ 的极化率

　　那么如何确定非好本征态如 $| n, l, m ⟩$ 的极化率呢？考虑 TDSE，根据绝热近似，若波函数初始处于 $| n, l, m ⟩$ ，需要先分解为好本征态的线性组合，

\begin{matrix} (15) & | n, l, m ⟩ = \sum_{α} c_{n, l, α, m} | n, α, m ⟩ . \end{matrix}

然后再考虑每个好本征态在电场中的变化。把经过电场扭曲后的

| n, l, m ⟩

记为

| n, l, m, * ⟩

，则

\begin{matrix} (16) & | n, l, m, * ⟩ = \sum_{α} c_{n, l, α, m} | n, α, m, * ⟩ . \end{matrix}

\begin{matrix} (17) & p_{(n, l, m), z} = - ⟨ n, l, m, * | z | n, l, m, * ⟩ = - \sum_{α} {| c_{n, l, α, m} |}^{2} ⟨ n, α, m, * | z | n, α, m, * ⟩ . \end{matrix}

其中近似认为

α \neq α^{'}

，

⟨ n, α^{'}, m, * | z | n, α, m, * ⟩ = 0

（子节 8 ）。在电场为零时，任意

p_{(n, l, m), z} = 0

，所以只有二阶修正起作用：

\begin{matrix} (18) & p_{(n, l, m), z} = \sum_{α} {| c_{n, l, α, m} |}^{2} p_{(n, α, m), z}^{2} . \end{matrix}

注意和电场成正比。

[1] ^ G. Drake, Springer Handbook of Atomic, Molecular, and Optical Physics (Springer-Verlag, New York, 2006).

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。

类氢原子斯塔克效应（微扰）

例 1 类氢原子 n=2 的斯塔克效应

例 2 氢原子斯塔克效应（能级截断）

例 3 氢原子的极化率（二阶微扰）

1. 含时问题

例 4 |n,l,m⟩ 的极化率

例 1　类氢原子 $n = 2$ 的斯塔克效应

例 2　氢原子斯塔克效应（能级截断）

例 3　氢原子的极化率（二阶微扰）

例 4　 $| n, l, m ⟩$ 的极化率