贡献者: 欄、停敘; addis
在发电厂中,有一种高大耸立的冷却装置,叫作 “冷却塔”(见 图 1 右侧)。乍一看,它像是两个圆台底朝底叠在一起,但仔细看会发现,它的边缘并非直线,而是略微弯曲的曲线。而与圆台相似,冷却塔的外形也通过一条特定的曲线绕着一条轴旋转得到。它之所以设计成这样,并不单单是为了好看,而是因为这样可以更好地抵抗大风、减少材料使用,还能提高散热效率。而这些效果,其实都和这条曲线在数学上的一些特殊性质有关。
图 1:冷却塔
在数学中,这类曲线早就被深入研究过。它由两条对称、互不相交的分支组成,虽然共用同一个坐标原点,但却分别朝着相反的方向无限延伸,永远不会相遇。这种曲线被称为 “双曲线”。很多读者第一次听到 “双曲线” 这个词,可能是在初中学习反比例函数的时候。当时常听到一句话:“反比例函数的图像是双曲线。” 那时候的理解可能还很简单,只是觉得图像上有 “两根” 弯曲的线条,所以叫 “双曲线”。至于它更深层的结构和性质,课堂上一般不会讲太细,学生自然也无从深入探究。
不过,相信读者还记得,反比例函数的图像有两条渐近线。那么,既然它是双曲线的图像,就可以合理猜想:双曲线也应该有两条渐近线。后面会说明,这个猜想是对的。虽然在高中阶段,“渐近线” 这个概念不常被强调,但它其实在双曲线中非常重要,前面所说冷却塔的特性,很大一部分就是基于双曲线与渐近线的关系。双曲线的两个分支会越来越靠近各自的渐近线,但始终不会真正相交。本文在介绍双曲线的过程中,也会进一步分析它和渐近线之间的关系,帮助读者更全面地理解这种特殊的曲线。
1. “反比例函数的图像是双曲线”
虽然 “双曲线” 作为一个几何概念相对陌生,但反比例函数却早已很熟悉了。既然反比例函数的图像其实就是双曲线的一种特殊情形,那么不妨从它出发,来看看这个熟悉的图像是如何逐步变化成 图 1 中冷却塔那样的形状。
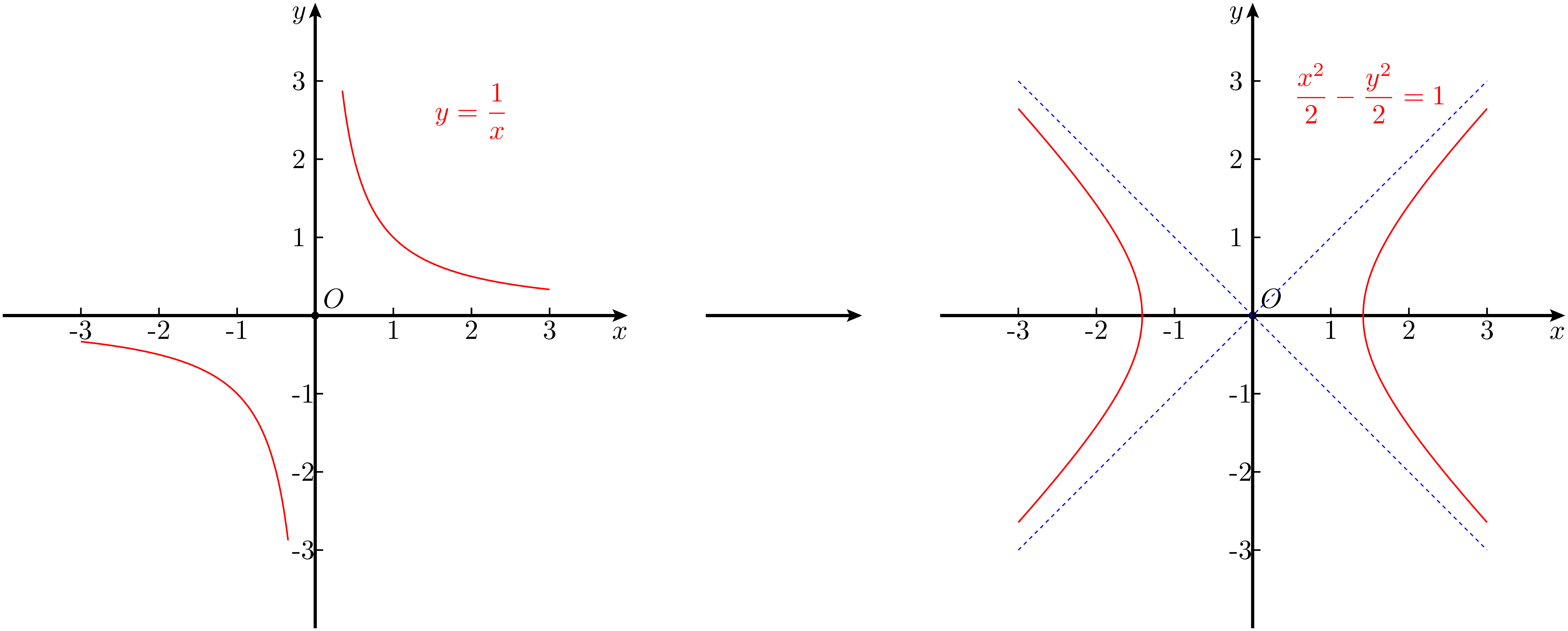
例 1 求反比例函数 $\displaystyle y={1\over x}$ 的图像逆时针旋转 $45^\circ$ 后的表达式。
根据图像旋转的规律,将 $\displaystyle y={1\over x}$ 逆时针旋转 $45^\circ$,即 $\displaystyle\theta=-{\pi\over4}$。
\begin{equation}
\begin{cases}
\displaystyle
X_0&=X_1 \cos \left(-{\displaystyle\frac{\pi}{4}}\right) + Y_1 \sin \left(-{\displaystyle\frac{\pi}{4}}\right)\\
Y_0&=Y_1 \cos \left(-{\displaystyle\frac{\pi}{4}}\right) - X_1 \sin \left(-{\displaystyle\frac{\pi}{4}}\right)\\
\end{cases}\implies
\begin{cases}
X_0&={\displaystyle\frac{1}{\sqrt{2}}}(X_1 - Y_1)\\
Y_0&={\displaystyle\frac{1}{\sqrt{2}}}(Y_1+ X_1) \\
\end{cases}~.
\end{equation}
将
式 1 代入 $xy=1$ 有:
\begin{equation}
\displaystyle
{1\over\sqrt{2}}(X_1 - Y_1)\cdot{1\over\sqrt{2}}(Y_1+ X_1)=1\implies {X_1^2\over2}- {Y_1^2\over2}=1~.
\end{equation}
即旋转后的方程是:
\begin{equation}
{x^2\over2}- {y^2\over2}=1~.
\end{equation}
图 2:旋转前后的图像
从 图 2 可以看出,旋转后的图像在 $y = 1$ 以下的部分,看起来就像一个矮胖的 “冷却塔”。由于旋转变换不会改变图形的形状,原本反比例函数图像的两条渐近线——$x$ 轴和 $y$ 轴,在旋转后变成了 $y = \pm x$。换句话说,图像虽然向两个方向无限延伸,但始终不会越过 $y = \pm x$ 这两条直线所形成的 “边界”。
再来看 式 3 ,这个式子的结构可能会让人感到眼熟。它和半径为 $\sqrt{2}$ 的圆的方程非常相似,唯一的不同是 $y^2$ 前的符号变了。这种细微的差异不禁让人联想到椭圆:椭圆的方程与圆的方程之间,也只是系数不同而已。然而,双曲线的图像与圆或椭圆看起来差别却很大,双曲线甚至都不是封闭的曲线,它们之间会存在什么联系呢?
2. 双曲线的几何定义
在研究椭圆时曾提到,若从圆的定义出发尝试推广,就需要对定义的表达方式进行调整。圆可以看作是满足 $|O_1P| = |O_2P| = r$ 的点的集合,其中第二个等号打开时,即只保证 $|O_1P| = |O_2P|$ 可以得到所有点关于两个定点的垂直平分线的集合;而如果 “打开” 第一个等号,将 $|O_1P| = r$ 和 $|O_2P| = r$ 视为两个独立的初始条件,而不再要求它们始终相等,那么就可以得到新的图形。
此时,如果固定两段距离的和为常数,即 $|O_1P| + |O_2P| = m$,就得到了椭圆。那么,如果将关注点转向两段距离的差,例如 $|O_1P| - |O_2P| = 0$,这看起来只是重新回到了 $|O_1P| = |O_2P|$,即垂直平分线的情形。但如果像椭圆那样固定这两个距离的差为一个非零常数 $m$,也就是说:$\left||O_1P| - |O_2P|\right| = m$,将会得到什么样的图形?
例 2 对两定点 $F_1(c, 0)$ 和 $F_2(-c, 0),(c>0)$,若点 $P$ 满足 $|PF_1| - |PF_2| = m,(0< m <2c)$,求 $P$ 方程。
解:
设点 $P$ 坐标为 $(x, y)$,根据题意有:
\begin{equation}
\sqrt{(x + c)^2 + y^2} - \sqrt{(x - c)^2 + y^2} = m~.
\end{equation}
移项后,两边平方有:
\begin{equation}
(x + c)^2 + y^2 = m^2 + 2m\sqrt{(x - c)^2 + y^2} + (x - c)^2 + y^2~.
\end{equation}
打开整理有:
\begin{equation}
2m\sqrt{(x - c)^2 + y^2}= 4cx - m^2~.
\end{equation}
两边平方,打开有:
\begin{equation}
4m^2(x^2 - 2cx+c^2) + 4m^2y^2= m^4-4m^2\cdot2cx+16c^2x^2~.
\end{equation}
整理后得到:
\begin{equation}
4(m^2 -4c^2)x^2 + 4m^2y^2= m^2(m^2-4c^2)~.
\end{equation}
两侧同时除以 $(m^2-4c^2)m^2$ 后得到:
\begin{equation}
\frac{x^2}{\left(\displaystyle\frac{m}{2}\right)^2} -\frac{y^2}{\displaystyle c^2-\left(\frac{m}{2}\right)^2}=1~.
\end{equation}
由于 $2c>m>0$,也就是 $\displaystyle c^2-\left(\frac{m}{2}\right)^2>0$。
需要注意的是,题目中的条件 $|PF_1| - |PF_2| = m > 0$ 隐含了一个默认关系,即:
\begin{equation}
|PF_1| > |PF_2|~.
\end{equation}
,因此题目的最终答案应该只包含 $x < 0$ 的区域,既:
\begin{equation}
\frac{x^2}{\left(\displaystyle\frac{m}{2}\right)^2} -\frac{y^2}{\displaystyle c^2-\left(\frac{m}{2}\right)^2}=1,\qquad(x<0)~.
\end{equation}
但显然,式 9 中的 $x$ 只有偶次方项,也就是说,它的图像应该是关于 $y$ 轴对称的。因此,在 $x> 0$ 的区域,还应该存在一个与左侧对称的图像,而这对应的其实就是 $|PF_2| > |PF_1|$ 的情况。因此,如果将条件改为 $||PF_1| - |PF_2|| = m$,其中 $0 < m < 2c$,就可以同时包括两侧的曲线,完整对应 式 9 的表达式。
可以看到,虽然题目把原本椭圆里 “不变量是两个距离的和” 改成了 “不变量是两个距离的差”,但对比 椭圆的推导过程 会发现,从 式 7 开始,两边推导出来的过程其实是一样的。真正的区别,只是参数的大小关系变了:椭圆里是 $m>2c$,而这里变成了 $m<2c$。为了让公式里的分母保持正数,最终式 9 和 椭圆的推导结果 的样子看上去才有了点差别。通常,为了方便记录,也为了与椭圆的写法统一,规定正号对应的参数记作 $a^2$,负号对应的参数记作 $b^2$。需要注意的是,这里的 $a$ 和 $b$ 的定义与椭圆中略有不同,没有要求两者绝对值的大小关系。根据这个约定,有:
\begin{equation}
\left(\displaystyle\frac{m}{2}\right)^2=a^2\qquad c^2-\displaystyle\left(\frac{m}{2}\right)^2=b^2~.
\end{equation}
整理可得:
\begin{equation}
m=2a\qquad a^2+b^2=c^2~.
\end{equation}
熟悉的平方和形式再次出现,不过这一次,$a,b,c$ 的位置发生了变化,这一点需要特别留意。
对比推导得到的 式 9 和 式 3 ,可以看到它们在形式上完全一致1。这也说明,式 9 的两条曲线其实就是双曲线。就这样,子节 1 是从反比例函数的角度认识双曲线,而此处则是从几何条件出发,推导出了双曲线的表达式。而题目中给出的条件,实际上正是双曲线的几何定义,也称为双曲线的第一定义。
定义 1 双曲线的几何定义
在平面上,所有满足到两个定点 $F_1$ 与 $F_2$ 的距离之差的绝对值为常数 $2a$ 的点 $P$ 的轨迹,构成一个几何图形,称为双曲线(hyperbola)。即,对于双曲线上的任意一点 $P$,都有:
\begin{equation}
||PF_1| - |PF_2|| = 2a ,\qquad(2a<|F_1F_2|)~.
\end{equation}
其中,$F_1$ 和 $F_2$ 被称为双曲线的两个
焦点(focus),两焦点之间的距离 $|F_1F_2|$ 称为椭圆的
焦距(focal distance),记作 $2c$,其中 $c$ 被称为
半焦距(semi-focal distance),也称为双曲线的
线性离心率(linear eccentricity)。
如之前所说,这个定义和椭圆的定义几乎没有什么区别。类似地,如果将 例 1 中两个定点设为 $F_1(0,-c)$ 和 $F_2(0,c)$,其中 $c>0$,相当于将原先的 $x$ 轴与 $y$ 轴互换,得到的表达式为:
\begin{equation}
\frac{y^2}{\left(\displaystyle\frac{m}{2}\right)^2}-\frac{x^2}{\displaystyle c^2-\left(\frac{m}{2}\right)^2} =1~.
\end{equation}
与椭圆不同的是,这里不仅分母位置发生了变化,参数的符号也需要随之调整。当然,不同点还体现在与坐标轴的交点个数上,标准椭圆与坐标轴有四个交点,而双曲线与坐标轴则只有两个交点。对于
式 9 ,令 $y=0$ 时,得到图像与 $x$ 轴的两个交点,采用
式 12 的记法为:
\begin{equation}
x = \pm a~.
\end{equation}
双曲线与坐标轴的交点称为
顶点(vertex),连接两个顶点的线段称为
实轴(transverse axis)2,长度为 $2a$,其中 $a$ 被称为
半实轴(semi-transverse axis)。与椭圆类似,双曲线的焦点也始终位于实轴上。
而令 $x=0$ 时,在实数范围内无解,这说明双曲线与 y 轴并无交点。不过在复数范围内有解:
\begin{equation}
y = \pm b \mathrm{i} ~.
\end{equation}
将复数解中虚部所对应的位置标在另一条坐标轴上,得到
虚顶点(co-vertex),连接两虚顶点的线段称为
虚轴(conjugate axis),长度为 $2b$,其中 $b$ 被称为
半虚轴(semi-conjugate axis)。
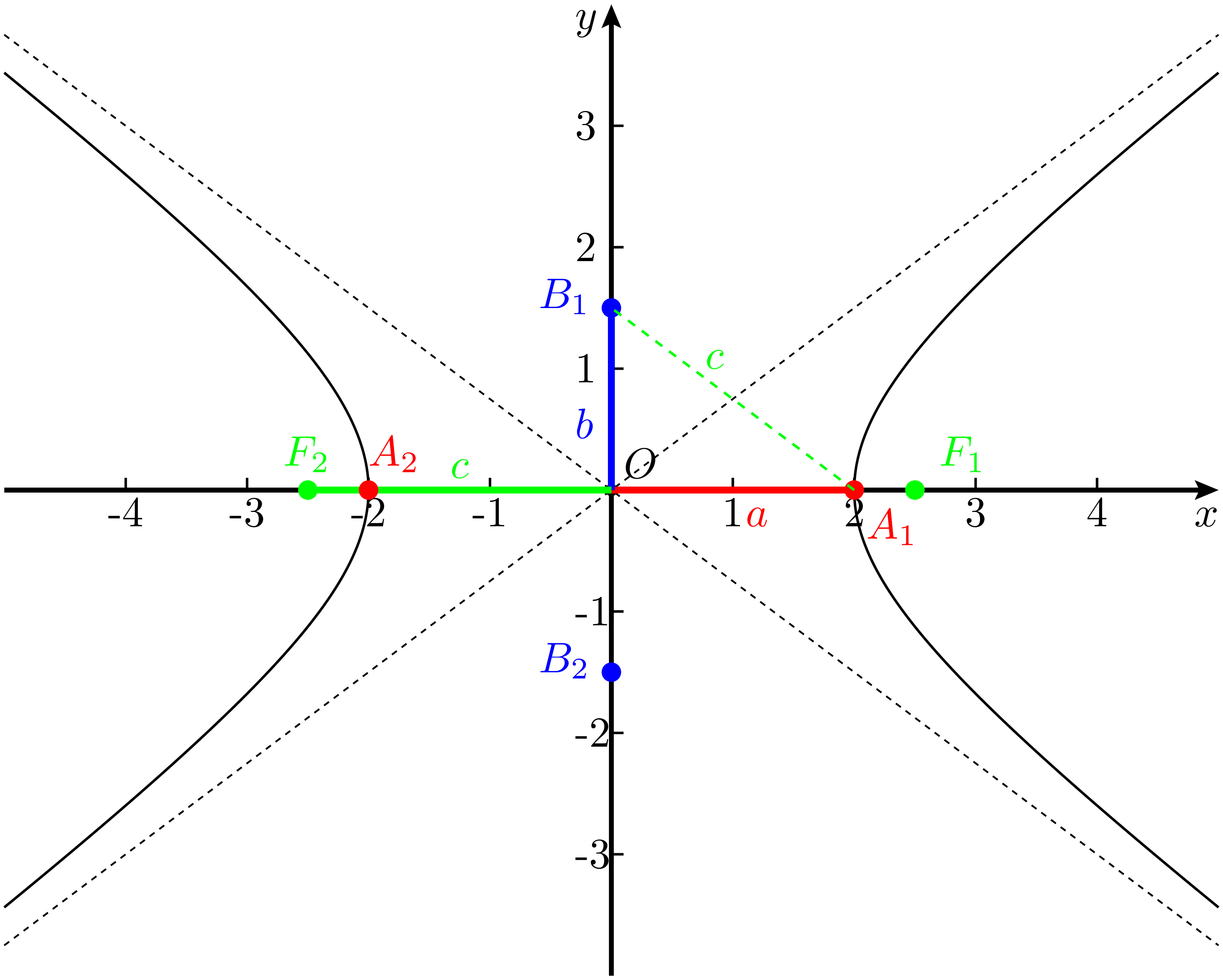
将虚、实顶点及式 13 中得到的 $a,b,c$ 的关系标记在图上,如图 3 所示。其中:$A_1,A_2$ 为实顶点,$B_1,B_2$ 为虚顶点,$F_1,F_2$ 为焦点。另外,通常把左右两侧的曲线整体看作一条双曲线,而把每一侧单独的部分称为一支,这里就分别叫做左支和右支。双曲线分割的平面中,称呼包含焦点的一侧称为双曲线的内部,包含虚轴的部分称为外侧。因此,与椭圆的中心在内部不同,双曲线的中心在外部。
图 3:$a,b,c$ 关系及虚、实顶点
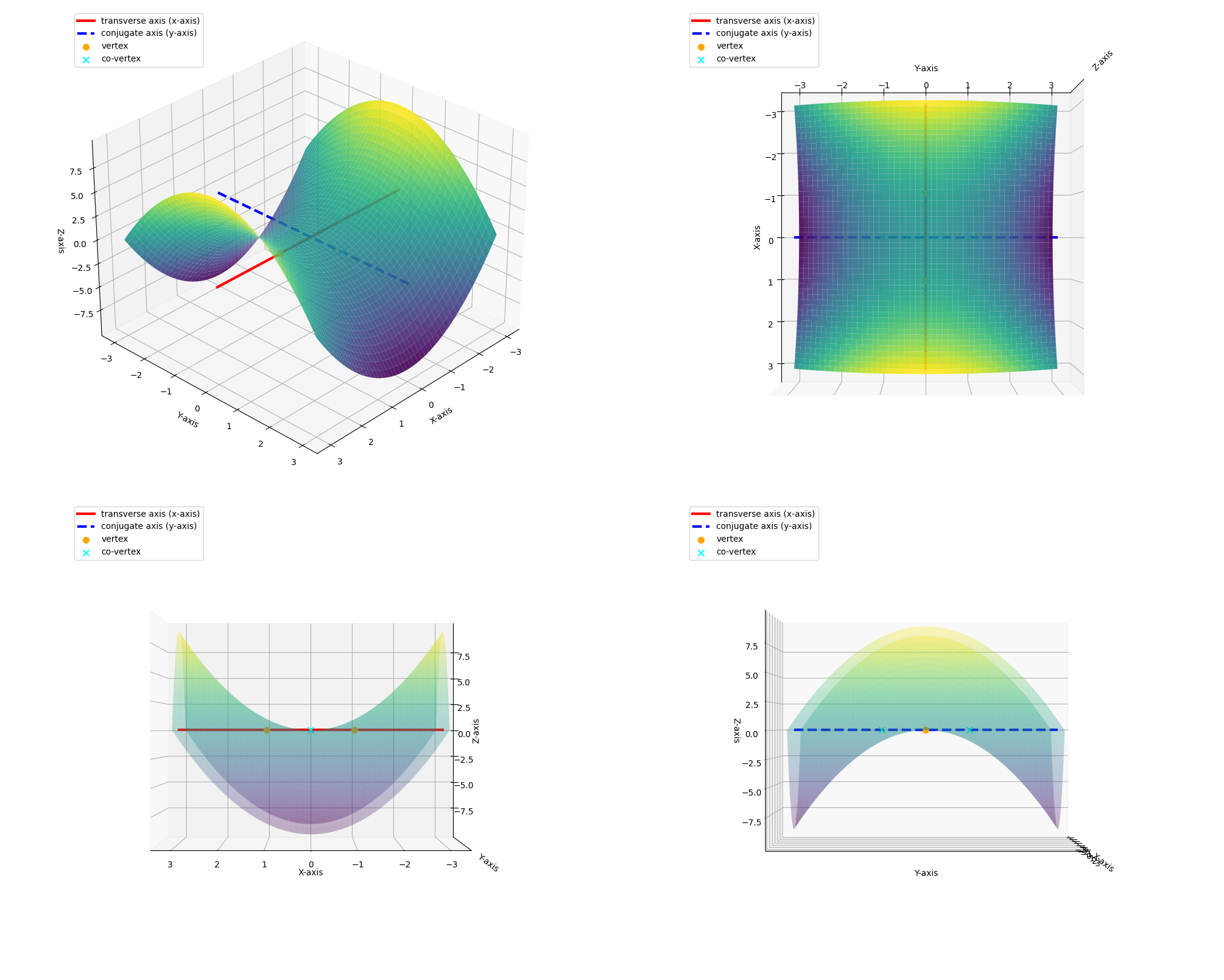
相信读者在这里可能会好奇:既然是 “虚” 的,为什么还要在图上标出来?虚顶点与双曲线,在图上看上去好像没什么关系?虚轴到底有什么用呢?其实,在更高阶段的数学中,比如复变函数的理论里,这些虚轴和虚顶点是有真实几何意义的。当把函数的定义域从实数扩展到复数后,它们对应的图形结构就会真正出现。当然这也与后面会介绍到的共轭双曲线有关系3。不过因为高中阶段暂时不涉及复变函数,所以这里只是简单提一提,满足一下对数学结构感兴趣的读者的好奇心。
图 4:复数域下的双曲线
3. 双曲线的方程
从式 9 和式 15 下手,整理代换后可以得到双曲线的标准方程:
定理 1 双曲线的标准方程
- 实轴在 $x$ 轴上,虚轴在 $y$ 轴上的双曲线标准方程4为:
\begin{equation}
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1,\qquad(a>0,b>0)~.
\end{equation}
- 实轴在 $y$ 轴上,虚轴在 $x$ 轴上的双曲线标准方程为:
\begin{equation}
\frac{y^2}{a^2} -\frac{x^2}{b^2} = 1,\qquad(a>0,b>0)~.
\end{equation}
再次提醒,需要注意 $a,b$ 与虚实轴的对应关系。特别地,如果 $a=b$,则称双曲线为等轴双曲线(equilateral hyperbola)。另外,如果保持 $x,y$ 对应的参数不变,只改变符号,也就是说,让虚轴和实轴交换位置,就会得到:
\begin{equation}
\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1,\qquad \frac{y^2}{b^2} - \frac{x^2}{a^2} = 1 ~.
\end{equation}
这时,称两条双曲线互为
共轭双曲线(conjugate hyperbola),如
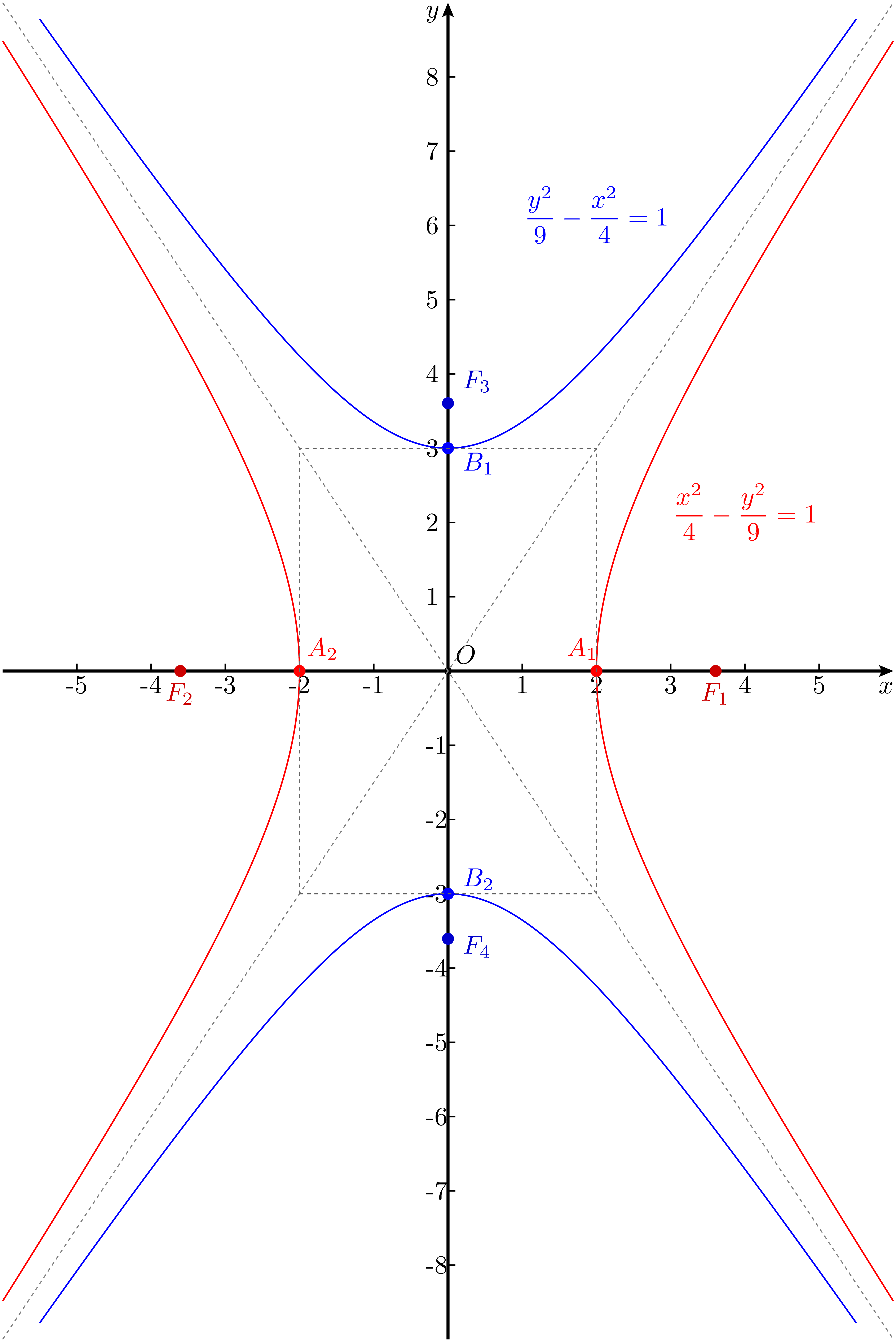
图 5 所示。这里的 “共轭” 一词,与复数中提到的共轭概念是同一个意思。简单来说,可以把
式 20 中右边的方程,看作是左边的方程等号右侧的 $1$ 变成 $-1$ 得到的。
图 5:共轭双曲线
从图中可以看到,这两条双曲线不仅交换了虚、实顶点和虚、实轴,而且它们有着相同的焦距,还共用同一组渐近线。
就像其他类型的方程一样,只要一个表达式符合双曲线标准方程的形式,就可以确定它的图像是双曲线。有了学习圆和椭圆时的经验,自然也会希望在这里也了解一下双曲线的参数方程。
在推导双曲线的参数方程时,可以使用三角函数中满足双曲线关系的 $\sec x$ 和 $\tan x$5,也可以更直接地使用双曲函数来表达。不过需要注意的是,双曲线的参数方程在高中阶段并不是必学内容,这里给出相关知识,主要是为了保证内容的完整性。
定理 2 *双曲线的参数方程
数学习惯上,参数方程往往只描述一条连续的轨迹。因此双曲线的参数方程只给出一支的部分。
- 实轴在 $x$ 轴上,虚轴在 $y$ 轴上的双曲线右支的参数方程6为:
\begin{equation}
\begin{cases}
x(t) = a \cosh t\\
y(t) = b \sinh t
\end{cases},\qquad t\in \mathbb{R} ~.
\end{equation}
\begin{equation}
\begin{cases}
x(\theta)=a\sec{\theta}\\
y(\theta)=b\tan{\theta}
\end{cases},\qquad \theta \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right) ~.
\end{equation}
- 实轴在 $y$ 轴上,虚轴在 $x$ 轴上的双曲线上支的参数方程为:
\begin{equation}
\begin{cases}
x(t) = b \sinh t\\
y(t) = a \cosh t
\end{cases},\qquad \theta\in \mathbb{R} ~.
\end{equation}
\begin{equation}
\begin{cases}
x(\theta) = b \tan \theta\\
y(\theta) = a \sec \theta
\end{cases},\qquad \theta \in \left( -\frac{\pi}{2}, \frac{\pi}{2} \right) ~.
\end{equation}
其中:$\cosh t$ 和 $\sinh t$ 等为双曲函数(hyperbolic functions)7,分别称作双曲余弦(hyperbolic cosine)和双曲正弦(hyperbolic sine)。它们的定义分别是
\begin{equation}
\cosh t = \frac{e^t + e^{-t}}{2}, \quad \sinh t = \frac{e^t - e^{-t}}{2}~.
\end{equation}
满足恒等关系:
\begin{equation}
\cosh^2 t - \sinh^2 t = 1~.
\end{equation}
可以联想到,双曲线的两条渐近线,其实正对应着正切函数或正割函数中的渐近线。另外,如果想要表述左支或下支,只需要将 $a$ 取为 $-a$ 即可。
双曲线族
与椭圆族类似,如果把双曲线标准方程右侧的 $1$ 替换为一个参数 $\lambda$,就可以得到一族双曲线:
\begin{equation}
\frac{x^2}{a^2} - \frac{y^2}{b^2} = \lambda,\qquad(\lambda>0)~.
\end{equation}
它代表着与双曲线 $\displaystyle\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ 具有相似性质的一组曲线。
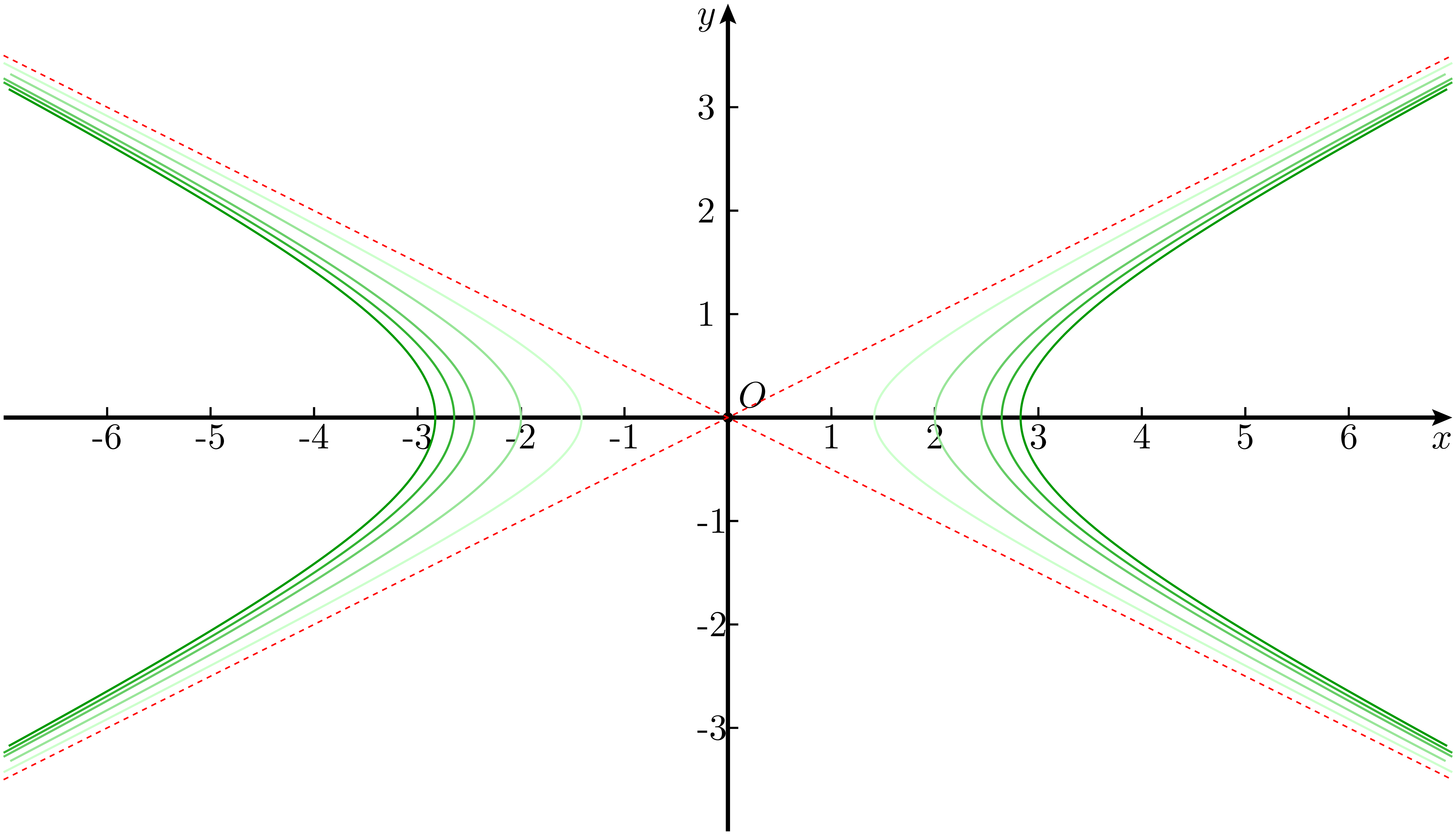
图 6:
式 27 取 $\lambda=0.5,1,1.5,1.75,2$ 时的图像
不过,与椭圆不同的是,双曲线并不要求 $\lambda$ 必须为正。事实上,只要 $\lambda\neq0$,就总能得到一条双曲线。当 $\lambda<0$ 时,令 $\eta=-\lambda$,可以得到:
\begin{equation}
\frac{y^2}{b^2}-\frac{x^2}{a^2} = \eta,\qquad(\eta>0)~.
\end{equation}
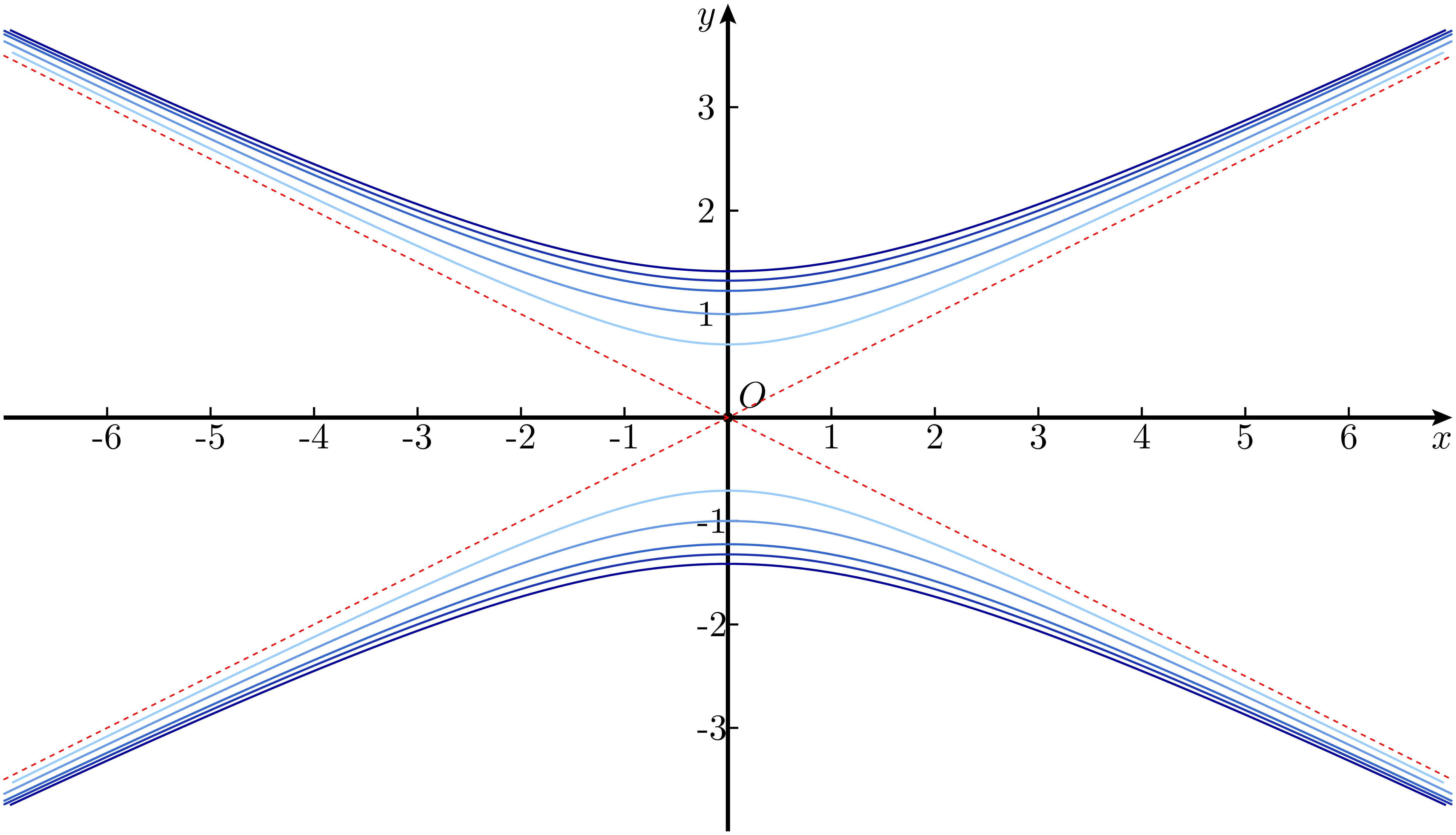
图 7:
式 28 取 $\eta=0.5,1,1.5,1.75,2$ 时的图像
因此,把它们放在同一个坐标系中,才能完整地表示出一个双曲线族:
\begin{equation}
\frac{x^2}{a^2} - \frac{y^2}{b^2} = \lambda,\qquad(\lambda\neq0)~.
\end{equation}
从图中可以很直观地看到,这些双曲线有一个共同的特点,就是它们都共享同一组渐近线8。前面提到的共轭双曲线,其实也属于同一个双曲线族。
4. 渐近线
在前面的内容中已经可以看出,渐近线是双曲线区别于椭圆、圆等曲线的重要特征之一。下面简单介绍一下双曲线的渐近线及其性质。
简单来说,渐近线(asymptotes)可以理解为图像在某个方向上不断靠近但永远不会到达的 “边界线” 或 “吸引线”。当沿着某个方向无限延伸时,双曲线和渐近线之间的距离会越来越小,最终在无穷远处趋近于零。相信读者在学习双曲线的过程中一定会产生两个问题:第一,为什么双曲线会有渐近线?第二,这些渐近线究竟是什么样的?或者说,它们的表达式是什么?
先来看第二个问题。其实在图 5 中就已初现端倪。从图中可以看到,双曲线的两条渐近线都经过一个由实顶点和虚顶点确定的矩形的四个顶点。具体来说,这两条渐近线经过点 $(a,b)$ 和 $(a,-b)$,并且也都通过原点。因此,可以写出它们的方程为:
\begin{equation}
y=\pm\frac{b}{a}x~.
\end{equation}
图 9:双曲线的渐近线
这也意味着,第一象限中渐近线与 $x$ 轴夹角 $\alpha$ 的正切值为 $\displaystyle\frac{b}{a}$。利用式 13 ,根据三角函数的等价关系可以得出:
\begin{equation}
\sin\alpha=\frac{b}{\sqrt{a^2+b^2}}=\frac{b}{c}~.
\end{equation}
这意味着,焦点到渐近线的距离 $l$ 恰好为:
\begin{equation}
l=c\sin\alpha = c\cdot \frac{b}{c} = b~.
\end{equation}
当然,前面渐近线表达式的推断主要是通过图像观察得出的,严格来说只能作为一种合理的猜想。如果对严谨地验证感兴趣,还可以越过高中知识的藩篱,到无穷远处看一看。
以标准方程式 18 为例,若想探究 $x$ 趋于正无穷时的情况,需要对式子进行变形,令分子中的 $x^2$ 消失,即变形为:
\begin{equation}
\frac{1}{a^2} - \frac{y^2}{x^2b^2} = \frac{1}{x^2} ,\qquad(a>0,b>0)~.
\end{equation}
当 $x$ 趋于无穷大时,右侧的 $\displaystyle\frac{1}{x^2}$ 会趋近于 $0$,可以忽略不计。而 $y$ 和 $x$ 都趋于无穷,因此左侧暂时不进行判断和处理。此时,将右侧变成 $0$ 之后,就可以移项化简了,可以得到:
\begin{equation}
\frac{1}{a^2} - \frac{y^2}{x^2b^2} = 0 \implies\frac{1}{a^2} = \frac{y^2}{x^2b^2}\implies \frac{1}{a} = \pm\frac{y}{xb}\implies y=\pm\frac{b}{a}x,\qquad(a>0,b>0)~.
\end{equation}
在开方时,为了保证正负两种可能性,方程中自然出现了 $\pm$ 符号。这就得到了式 30 。而在式 34 中可以发现,在无穷远处双曲线 $x$ 和 $y$ 的增长速率保持一个固定比例,可以近似认为是稳定的,而这也就解答了前面提到的第一个问题——正是 $x$ 和 $y$ 在无穷远处保持了固定的比例关系,才会出现渐近线。当然,在大学阶段学习了泰勒展开后,可知当 $u\to 0$ 时,有9:
\begin{equation}
\sqrt{1+u} = 1+\frac{1}{2}u+ \mathcal{O}\left(u \right) ~.
\end{equation}
进而,可以给出更严谨些的证明:
由标准方程式 18 变形,可得:
\begin{equation}
y = \pm\frac{bx}{a} \sqrt{1-\frac{a^2}{x^2}}~.
\end{equation}
当 $x\to+\infty$ 时,$-\displaystyle\frac{a^2}{x^2}\to0$,将 $\displaystyle u=-\frac{a^2}{x^2}$ 代入式 35 并将整体带入式 36 有:
\begin{equation}
\begin{split}
y &= \pm\frac{bx}{a}\left(1-\frac{1}{2}\frac{a^2}{x^2}+ \mathcal{O}\left(-\frac{a^2}{x^2} \right) \right)\\
&=\pm\frac{bx}{a} \mp\frac{bx}{a} \cdot\frac{a^2}{2x^2}\mp\frac{bx}{a} \mathcal{O}\left(\frac{1}{x^2} \right) \\
& = \pm\frac ba x \mp \frac{ab}{2x} \mp \mathcal{O}\left(\frac{1}{x} \right) ~.
\end{split}
\end{equation}
当 $x\to\infty$ 时,就有 $\displaystyle\mp \frac{ab}{2x} \mp \mathcal{O}\left(\frac{1}{x} \right) \to0$,从而自然就得到了
式 30 。
当然,对于渐近线的深入研究远远超出了高中的知识范畴,如果感兴趣也可以参考渐近线了解,在此就不予赘述了。
不过,双曲线的渐近线与双曲线上的任意点所确定的平行四边形面积是一个固定值。其实,这一点可以从反比例函数的图像中看出端倪——在反比例函数 $\displaystyle y={k\over x}$ 图像上的任意一点,向 $x$ 轴和 $y$ 轴作垂线,会与坐标轴围出一个面积相等的矩形。
例 3 求:双曲线上任意一点,向两条渐近线作平行线,与两渐近线围成的平行四边形的面积。
不妨设双曲线上的一点 $P(x_0, y_0)$ 满足:
\begin{equation}
\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}=1~.
\end{equation}
点 $P$ 到渐近线 $\displaystyle y = \frac{b}{a}x$ 的距离是所求平行四边形的高 $h$,根据点到直线的距离公式,有:
\begin{equation}
h=\frac{\left|\displaystyle{b\over a}x_0-y_0\right|}{\displaystyle\sqrt{{b^2\over a^2}+1}}=\frac{b\left|\displaystyle \displaystyle{x_0\over a}-{y_0\over b}\right|}{\displaystyle\sqrt{{b^2\over a^2}+1}}~.
\end{equation}
再作过 $P$ 与 $\displaystyle y = \frac{b}{a}x$ 平行的直线,令其与渐近线 $\displaystyle y = -\frac{b}{a}x$ 相交于点 $Q(x_1, y_1)$,则 $Q$ 满足:
\begin{equation}
\begin{cases}
y_1-y_0=\displaystyle{b\over a}(x_1-x_0)\\
y_1=\displaystyle-{b\over a} x_1
\end{cases}~.
\end{equation}
于是,线段 $PQ$ 的长度就是平行四边形中与 $h$ 对应的底 $a$,可表示为:
\begin{equation}
\begin{split}
a&=\sqrt{(x_1-x_0)^2+(y_1-y_0)^2}\\
&=\sqrt{(x_1-x_0)^2+{b^2\over a^2}(x_1-x_0)^2}\\
&=|x_1-x_0|\sqrt{1+{b^2\over a^2}}~.
\end{split}
\end{equation}
整理 式 40 可得:
\begin{equation}
x_1-x_0=-\frac{a}{2}\left(\displaystyle{x_0\over a}+{y_0\over b}\right)~.
\end{equation}
综上有,平行四边形的面积为:
\begin{equation}
\begin{split}
S&=ah\\
&=\left|-\frac{a}{2}\left(\displaystyle{x_0\over a}+{y_0\over b}\right)\right|\sqrt{1+{b^2\over a^2}}\cdot\frac{b\left|\displaystyle \displaystyle{x_0\over a}-{y_0\over b}\right|}{\displaystyle\sqrt{{b^2\over a^2}+1}}\\
&=\frac{ab\left|\displaystyle\frac{x_0^2}{a^2}-\frac{y_0^2}{b^2}\right|}{2}\\
&=\frac{ab}{2}~.
\end{split}
\end{equation}
根据 例 1 的推导可知,反比例函数 $\displaystyle y = \frac{k}{x}$ 经过逆时针旋转 $45^\circ$ 后,其对应的双曲线表达式为:
\begin{equation}
{x^2\over(\sqrt{2k})^2}- {y^2\over(\sqrt{2k})^2}=1~.
\end{equation}
这说明此时 $a = b = \sqrt{2k}$,也就是说,两条渐近线互相垂直,因此围成的平行四边形就是一个矩形。根据 式 43 ,面积为:
\begin{equation}
\frac{ab}{2} = \frac{\sqrt{2k} \cdot \sqrt{2k}}{2} = k~.
\end{equation}
5. 双曲线的性质
双曲线的反射性质
定理 3 双曲线反射性质
对于一条双曲线,其两个焦点为 $F_1$ 和 $F_2$。对于双曲线上的任意一点 $P$,若从 $F_1$ 发出一条光线射向 $P$,在 $P$ 发生镜面反射,则反射光线的反向延长线将经过 $F_2$。也就是说,直线 $PF_1$ 与 $PF_2$ 关于切线 $l$ 对称,即:
\begin{equation}
\angle(F_1P, l) = \angle(PF_2, l)~.
\end{equation}
或者换句话说,对于法线 $n$,有
\begin{equation}
\angle(F_1P, n) = \angle(PF_2, n)~.
\end{equation}
其中 $l$ 是点 $P$ 处的切线,$n$ 是 $P$ 处的法线方向。
双曲线的反射性质与椭圆非常相似,都是指反射光线所在的直线会经过另一个焦点。它们之间的区别仅在于:对于椭圆,反射光线可以实际到达另一个焦点;而对于双曲线,反射光线本身不会直接到达另一个焦点,而是其反向延长线穿过另一个焦点。
与椭圆的证明方法类似,也可以从几何角度解释为什么双曲线具有这样的反射性质。在正式证明之前,需要先得到引理 1 的结论。
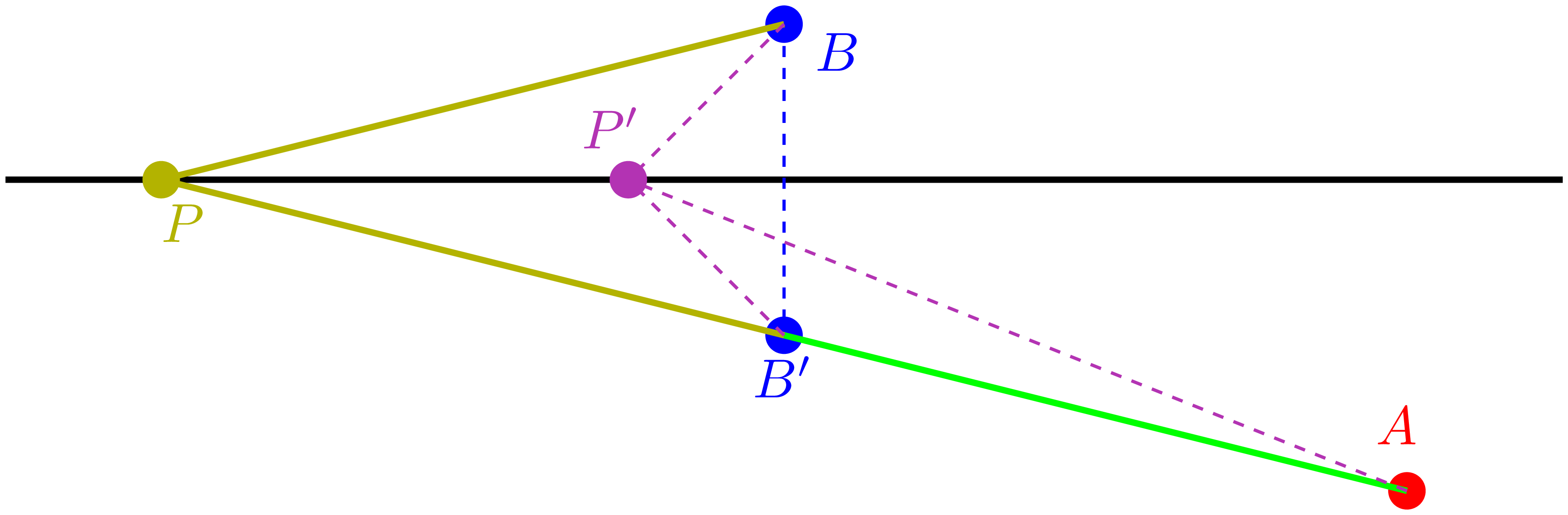
引理 1 设在直线 $l$ 两侧的点 $A,B$,满足二者到 $l$ 的距离不相等,那么对于直线上的一点 $P$,当且仅当 $l$ 平分 $\angle APB$ 时,$||PA|-|PB||$ 取到最大值。
设 $B'$ 是点 $B$ 关于直线 $l$ 的对称点。那么对于任意点 $P \in l$,都有 $|PB| = |PB'|$,且直线 $B'P$ 与 $BP$ 关于直线 $l$ 对称。
图 10
根据三角形的边长关系,在 $\triangle APB'$ 中有:
\begin{equation}
||AP|-|BP||=||AP|-|B'P||\leq|AB'|~.
\end{equation}
当且仅当 $P$ 与 $AB'$ 共线时,等号成立,此时 $||AP|-|BP||$ 取到最大值。而结合前面的对称关系,可以得出,此时直线 $AP$ 与 $BP$ 关于直线 $l$ 对称,即 $l$ 平分 $\angle APB$。
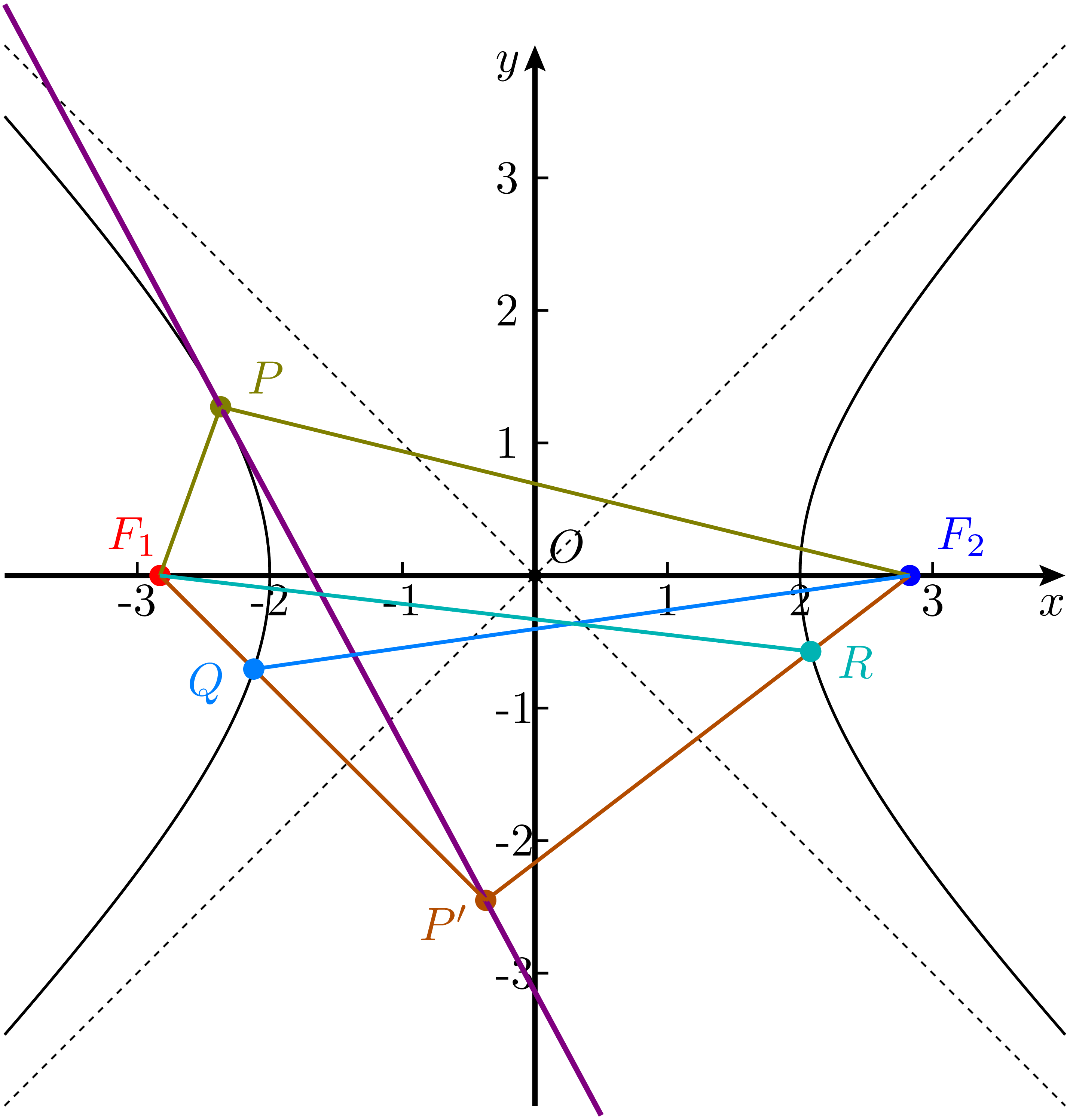
有了引理的支持,证明过程就比较容易了。设 $P$ 是双曲线上的任意一点,$l$ 是过 $P$ 的切线,在 $l$ 上任取另一点 $P'$($P'\neq P$),连接 $PF_1$、$PF_2$ 以及 $P'F_1$、$P'F_2$。由于 $P'$ 在双曲线外部,而 $F_1,F_2$ 位于双曲线内部,因此线段 $P'F_1,P'F_2$ 必定与双曲线两支分别交于某一点,假设 $P$ 和 $Q$ 位于双曲线的同一支上,$P$ 和 $R$ 位于双曲线的不同支上。不妨设 $P$ 在 $F_1$ 一侧,则满足:
\begin{equation}
|P'F_1|=|P'Q|+|QF_1|,\qquad |P'F_2|=|P'R|+|RF_2|~.
\end{equation}
且根据双曲线的几何定义,有:
\begin{equation}
|PF_2| - |PF_1|=|QF_2| - |QF_1|=|RF_1|-|RF_2|=2a>0~.
\end{equation}
连接 $QF_2,RF_1$ 可以得到图 11 。
图 11:证明反射性质
根据三角形两边之和大于第三边,在 $\triangle QP'F_2$ 和 $\triangle RP'F_1$ 中,分别有:
\begin{equation}
|QF_2| + |P'Q| > |P'F_2|~.
\end{equation}
\begin{equation}
|RF_1| + |P'R| > |P'F_1|~.
\end{equation}
结合式 49 式 50 和式 51 有:
\begin{equation}
|P'F_2| - |P'F_1|<(|QF_2| + |P'Q|)-(|P'Q|+|QF_1|)=|QF_2|-|QF_1|=2a~.
\end{equation}
结合式 49 式 50 和式 52 有:
\begin{equation}
|P'F_1|-|P'F_2|<(|RF_1| + |P'R|)-(|P'R|+|RF_2|)=|RF_1|-|RF_2|=2a~.
\end{equation}
综上有10:
\begin{equation}
||P'F_1|-|P'F_2||<2a=||PF_2| - |PF_1||~.
\end{equation}
由于 $P'$ 的任意性,可以推知,切点 $P$ 是直线 $l$ 上唯一一个使得与 $F_1$、$F_2$ 的距离之差取得极大值的位置。因此,根据引理 1 ,可以得出结论:连接 $P$ 到 $F_1$ 和 $F_2$ 的直线关于切线 $l$ 对称,也就是说,入射方向 $PF_1$ 和反射方向 $PF_2$ 关于切线对称,符合反射的定义。又由于 $P$ 是任取的双曲线上的点,因此双曲线上的所有点都满足这一反射规律。
双曲线的弦
同样地,连接双曲线上任意两点的线段称为弦。不过,由于双曲线有两支的特性,弦可能位于双曲线的内部,也可能出现在双曲线的外部。但需要注意的是,由于双曲线是一个二次方程,它与任意一条直线联立后,最多只能得到两个实数解,因此弦所在的直线与双曲线最多只有两个交点,不会出现跨越双曲线两支的情况。
与椭圆类似,通过一个焦点且垂直于实轴的弦,称为通径(latus rectum)。
例 4 求双曲线通径的长度
以右焦点 $F(c,0)$ 为例,通径所在的直线为 $x=c$。将其代入双曲线方程,得
\begin{equation}
\frac{c^2}{a^2} - \frac{y^2}{b^2} = 1~.
\end{equation}
将
式 13 代入上式得:
\begin{equation}
\frac{a^2 + b^2}{a^2} - \frac{y^2}{b^2} = 1~,
\end{equation}
整理可得:
\begin{equation}
\frac{y^2}{b^2} = \frac{b^2}{a^2}~,
\end{equation}
因此,通径两个端点的纵坐标为:
\begin{equation}
y = \pm \frac{b^2}{a}~.
\end{equation}
综上,根据双曲线的对称性,所有通径的长度都为 $\displaystyle\frac{2b^2}{a}$。
另外,类似地也可以证明,在双曲线上的所有点中,到某一焦点距离最近的位置就是它同侧的顶点。
例 5 证明:对于双曲线 $\displaystyle\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1$ 上任意一点 $P(x_0, y_0)$,若右焦点为 $F(c, 0)$,则当 $|PF|$ 取得最小值时,$P$ 为右支的顶点。
首先可以注意到,如果 $P$ 在左支上,那么取 $P$ 关于 $y$ 轴对称的点 $P'$,显然有 $|P'F| < |PF|$,因此最小值不可能出现在左支上,$P$ 必须在右支上。
根据两点间距离公式,有:
\begin{equation}
d=\sqrt{(x_0-c)^2+y_0^2}~.
\end{equation}
由双曲线方程变形可得:
\begin{equation}
y_0^2 = \frac{b^2}{a^2}x_0^2 - b^2~.
\end{equation}
由于 $d \geq 0$,可以考虑 $d^2$,将 式 61 和 式 13 代入得:
\begin{equation}
\begin{split}
d^2 &= (x_0 - c)^2 + y_0^2 \\
&= x_0^2 - 2cx_0 + c^2 + \frac{b^2}{a^2}x_0^2 - b^2 \\
&= \frac{1}{a^2} \left( c^2x_0^2 - 2ca^2x_0 + a^4 \right) \\
&= \frac{1}{a^2} \left( cx_0 - a^2 \right)^2~.
\end{split}
\end{equation}
由此可见,当 $\displaystyle x_0 = \frac{a^2}{c}$ 时,$d^2$ 取得极小值。但由于 $c > a$,所以 $\displaystyle x_0 = a \cdot \frac{a}{c} < a$,该点并不在双曲线上。
又因为 式 62 在区间 $\left( \displaystyle\frac{a^2}{c}, +\infty \right)$ 上是单调递增的,所以在 $x_0 = a$ 处取得最小值。此时,$P$ 就是右支的顶点。
切线
根据介绍过的隐函数求导法,容易得到双曲线作为隐函数的导数为:
\begin{equation}
\frac{2x}{a^2} - \frac{2yy'}{b^2} = 0~.
\end{equation}
即双曲线上某点 $(x_0,y_0)$ 处,切线斜率为 $\displaystyle\frac{b^2}{a^2}\frac{x_0}{y_0}$,这也可以通过连立直线与双曲线的方程,然后按照只有一个交点的方法得到。有了斜率之后,也可以采用解析几何的方法来验证双曲线的反射性质。
另外,根据点斜式,可以整理得到双曲线的切线方程为:
\begin{equation}
\frac{xx_0}{a^2} - \frac{yy_0}{b^2} = 1~.
\end{equation}
与椭圆一样,就像是在双曲线的方程中,把一个 $x$ 和一个 $y$ 分别替换成了椭圆上某个固定点的坐标 $(x_0, y_0)$,就能直接写出该点处的切线方程。
双曲线的切线总是指向渐近线的外侧。虽然这个现象从图像上看非常直观,但实际上是可以给出严格证明的,参见例 6 。其他情形的证明方法也类似。
例 6 证明:对于第一象限中实轴在 $x$ 轴的双曲线,切线的斜率总是大于渐近线的斜率。
双曲线上的点 $(x_0, y_0)$ 满足:
\begin{equation}
\frac{x_0^2}{a^2} - \frac{y_0^2}{b^2} = 1\quad\implies\quad b^2x_0^2=a^2y_0^2+a^2b^2~.
\end{equation}
现已知,切线的斜率为:
\begin{equation}
k_1 = \frac{b^2}{a^2}\frac{x_0}{y_0}~.
\end{equation}
而渐近线的斜率为:
\begin{equation}
k_2 = \frac{b}{a}~.
\end{equation}
显然,$k_1 > 0$,$k_2 > 0$。为了比较两者的大小,引入一个比值 $q$:
\begin{equation}
q=\frac{k_1}{k_2}
=\frac{\displaystyle\frac{b^2}{a^2}\frac{x_0}{y_0}}{\displaystyle\frac{b}{a}}
=\frac{bx_0}{ay_0}~.
\end{equation}
比较 $q$ 和 $1$ 的大小关系,就可以判断 $k_1$ 和 $k_2$ 的大小。为了简化运算,这里计算 $q^2$,因为 $q>0$,所以 $q^2$ 与 $q$ 的大小关系一致。由计算得:
\begin{equation}
q^2 = \frac{b^2x_0^2}{a^2y_0^2}
= \frac{a^2y_0^2 + a^2b^2}{a^2y_0^2}
= 1 + \frac{b^2}{y_0^2} > 1~.
\end{equation}
因此,可以得出 $q>1$,也就是 $k_1>k_2$。此外,从式 69 可以看出,当 $y_0$ 趋于无穷大时,$q$ 逐渐趋近于 $1$,就意味着切线的斜率和渐近线的斜率最终接近。
1. ^ 例如 $\displaystyle\left( \frac{m}{2} \right)^2 = c^2 - \left( \frac{m}{2} \right)^2 = 2\implies m = 2\sqrt{2}, c = 4$。
2. ^ 注意区分这里与复平面中 “实轴” 和 “虚轴” 的含义不同。
3. ^ 对比图 4 中左上角的图和图 5 ,可以发现它们的形状非常相似,这并不是巧合,而是共轭的含义背后自然体现出来的结果。
4. ^ 也称为焦点在 $x$ 轴上的双曲线标准方程,下面同理。
5. ^ 参见函数视角下的三角函数
6. ^ 也称为焦点在 $x$ 轴上的双曲线参数方程,下面同理。
7. ^ 类似于三角函数,双曲函数也有一些恒等关系。因而借用了正弦、余弦、正切等名称,具体可参见双曲函数。
8. ^ 当然,还有另一个共同点是它们的离心率也相同。
9. ^ 关于 $ \mathcal{O}\left(u \right) $ 可暂时理解为 $0$,在高中阶段不涉及。
10. ^ 此处其实可以得到结论,双曲线外侧的点到两焦点距离之差的绝对值小于 $2a$。类似地,也可以证明双曲线内侧的点到两焦点距离之差的绝对值大于 $2a$。