圆锥曲线的统一定义（高中）

贡献者：欄、停敘

预备知识　圆锥曲线与圆锥，函数的变换

　　在圆锥曲线与圆锥中曾提到，古希腊时期，人们通过截取圆锥面，得到了圆、椭圆、抛物线和双曲线这四类曲线，它们后来被统称为 “圆锥曲线”。这种从几何构造出发的方法，直观地揭示了它们的共同起源。然而，尽管阿波罗尼乌将它们放入了同一个圆锥面，在后来一千多年的研究中却仍然被当作彼此独立的对象来看待。无论是图像形状还是代数表达式，它们看起来都完全不同，彼此之间似乎没有直接联系。这种割裂也延续到了现代教学中。

　　以椭圆为例，高中教材通常在介绍完长轴、短轴、焦点等要素之后，会突然引入一个叫 “离心率” 的量¹，并简单解释为 “衡量椭圆扁平程度的参数”。它的定义是一个比值，看起来更像三角函数的形式，而不像之前那些能直接对应到具体图形的长度。更令人疑惑的是，不只是椭圆，抛物线和双曲线也各有自己的离心率。这不禁让人想问：为什么所有圆锥曲线都有离心率？这个量到底意味着什么？不同曲线之间的离心率又有什么关系？

　　这类困惑其实很正常。毕竟，在长轴、焦点等概念被提出的年代，离心率这个概念还没有出现，那时的研究更关注图形本身，而不是参数之间的抽象联系。也正因为如此，当它和其他几何要素一同出现在课本中时，常常会让人感到有些突兀。

　　随着解析几何的发展，数学家们发现，这些看似不同的圆锥曲线，在引入一个定点和一条定直线后，竟然可以通过一个简洁而优雅的定义统一起来。从这个统一的角度出发，离心率不再是某种 “空降” 的数值，而是整个几何结构的内在参数。更重要的是，这一定义不仅回答了之前的问题，更在射影几何等更深层的理论中展现出非凡的结构美感。遗憾的是，这部分内容在现行高中课程中已被完全删去。为了带给读者获得更全面的视角，本文将从统一定义出发，系统梳理圆锥曲线的几何构造及其背后隐藏的深层联系。

1. 关于统一定义的思考

　　初中阶段学过，矩形和菱形都是平行四边形的特殊情况。而前文也提到了，圆、椭圆、抛物线和双曲线也有着相同的几何起源——它们都可以看作是平面截取圆锥面后所形成的轨迹。它们之间的区别，仅仅在于截面与圆锥的母线或对称轴之间的夹角满足不同的条件。既然这些曲线本质上出自同一个构造，便很自然地会想到，它们应当可以用一种统一的方式加以描述。现有的不同代数表达式，可能只是这种统一形式在参数取值不同情况下的具体表现。

　　既然目标是寻找一种统一的表达形式，参照初中对平行四边形的处理思路，首先要做的就是提取三种曲线定义中的共同要素。回顾定义可发现，唯一在椭圆、抛物线和双曲线中都明确出现的，是 “焦点”。这表明，焦点应该会出现在统一定义之中。

　　与焦点直接相关的参数主要有两类：椭圆和双曲线中使用的是两个焦点之间的距离（焦距 $2c$），而抛物线则使用焦点到准线的距离（焦准距 $p$）。很显然，若要建立统一的定义，要么将椭圆和双曲线纳入抛物线的定义框架中，要么反过来，将抛物线纳入椭圆与双曲线的定义框架中。这就引出了一个关键选择：是为抛物线补上第二个焦点，还是为椭圆和双曲线补上一条与焦点对应的准线，然后忽略一个焦点？

2. 圆锥曲线的 “焦点-准线” 定义

　　 开普勒（Kepler）关于行星运动的研究为前面的问题提供了一个重要的启发。他起初与同时代的许多人一样，认为行星的轨道是圆形的。但在利用第谷·布拉赫（Tycho Brahe）留下的高精度观测数据反复检验后发现，只有当轨道是一个椭圆，且太阳位于其中一个焦点上时，才能与观测结果严格吻合——这就是著名的 “开普勒第一定律”。

　　值得注意的是，轨道所在的椭圆中的另一个焦点只是几何上的构造点，并不对应任何实际存在的天体。因此，在这个物理模型中，一个焦点具有实际意义，而第二个焦点则并非必需。天文学家据此总结出，行星的轨道可以看作是一个点与某种约束条件下的轨迹，即使圆轨道也能纳入这种描述方式。而牛顿（Newton）给出了 “约束条件” 的具体形式——万有引力定律——不过这是后来的故事了。

　　不过，上面的路径也带来了一个启示：既然椭圆中的一个焦点只是辅助构造，那么看上去好像可以在椭圆和双曲线中忽略掉一个焦点，转而人为引入一条 “准线” 作为约束，基于 “焦点–准线” 的结构，实现圆锥曲线的统一定义。

推导与验证

　　既然希望将椭圆和双曲线纳入抛物线的定义框架，不妨先回顾抛物线的定义：设点 $P$ 到定点 $F$ 的距离为 $|PF|$，到定直线 $L$ 的距离为 $|PL|$，那么满足

\begin{equation} |PF| = |PL|~. \end{equation}

的点的轨迹，就是抛物线。

　　参考之前从圆的定义出发推广其他圆锥曲线的思路，若要得到统一定义，只需保留原有的表达形式，并将这个唯一的约束条件式 1 转写为一个包含参数的等价形式，使不同的参数值对应不同的曲线。一个自然的做法是，仿照阿波罗尼斯圆的方式，将其推广为：

\begin{equation} \frac{|PF|}{|PL|} = e,\quad(e>0)~. \end{equation}

　　这样当参数 $e = 1$ 时，自然就得到抛物线。接下来，将探究在 $e \ne 1$ 的情形下，这个轨迹将对应怎样的曲线。

例 1　设点 $F(m,0)$，直线 $L : x = m - p,(p>0)$。²若点 $P(x,y)$ 满足式 2 ，且 $e\neq 1$，求点 $P$ 的轨迹方程。

　　解：

　　根据点到直线和两点之间的距离公式，有：

\begin{equation} \frac{\sqrt{(x - m)^2 + y^2}}{|x - m + p|} = e~. \end{equation}

　　由于 $e > 0$，可直接两边平方并整理，得到：

\begin{equation} \begin{split} &(x - m)^2 + y^2 = e^2(x - m + p)^2\\ \implies &(1 - e^2)x^2 + y^2 = 2[m - e^2(m - p)]x + [e^2(m - p)^2 - m^2]~. \end{split} \end{equation}

　　为了让结果恰巧关于 $y$ 轴对称，可令一次项系数为零，即：

\begin{equation} m - e^2(m - p) = 0\implies e^2(m - p)^2 = \frac{m^2}{e^2}~. \end{equation}

　　（这里如果不理解，也可以通过配方，将式 4 变形为

\begin{equation} (1 - e^2)\left(x+m+\frac{pe^2}{1-e^2}\right)^2 + y^2 = \frac{p^2 e^2}{1 - e^2}~. \end{equation}

，根据二次函数的知识，$\displaystyle\left(x+m+\frac{pe^2}{1-e^2}\right)^2$ 的对称轴为 $\displaystyle x=-m-\frac{pe^2}{1-e^2}$。因此，通过调整 $m$ 的值来调整对称轴。）

　　此时有：

\begin{equation} m = -\frac{pe^2}{1 - e^2}, \qquad m-p= -\frac{p}{1 - e^2}~. \end{equation}

　　将上述结果代入式 4 ，可得：

\begin{equation} \begin{split} &(1 - e^2)x^2 + y^2 = \frac{m^2}{e^2}(1 - e^2) = \frac{p^2 e^2}{1 - e^2}\\ \implies&\frac{x^2}{\displaystyle\frac{p^2 e^2}{(1 - e^2)^2}} + \frac{y^2}{\displaystyle\frac{p^2 e^2}{1 - e^2}} = 1~. \end{split} \end{equation}

　　讨论：

当 $0 < e < 1$ 时，式 8 形式上符合椭圆的标准方程，可以得到如下参数对应关系：
\begin{equation} a = \frac{p e}{1 - e^2}, \qquad b = \frac{p e}{\sqrt{1 - e^2}}~. \end{equation}
显然 $a > b$，因此点 $P$ 的轨迹是一个长轴沿 $x$ 轴方向的椭圆。又根据式 7 可知点 $F$ 在 $x$ 轴负半轴，准线 $L$ 在 $F$ 左侧，也在 $x$ 轴负半轴。结合椭圆的参数关系有：
\begin{equation} c = \sqrt{a^2 - b^2} = \frac{p e^2}{1 - e^2}~, \end{equation}
与式 7 对比可知，$F$ 正是椭圆的一个焦点。另外，由于 $a = e |m - p| < |m - p|$，说明准线 $L$ 在椭圆之外。
当 $e > 1$ 时，式 8 可整理为：
\begin{equation} \frac{x^2}{\displaystyle\frac{p^2 e^2}{(e^2 - 1)^2}} - \frac{y^2}{\displaystyle\frac{p^2 e^2}{e^2 - 1}} = 1~, \end{equation}
这符合双曲线的标准方程。此时的参数对应关系为：
\begin{equation} a = \frac{p e}{e^2 - 1}, \qquad b = \frac{p e}{\sqrt{e^2 - 1}}~. \end{equation}
因此，点 $P$ 的轨迹是一个实轴沿 $x$ 轴方向的双曲线。由式 7 可知，点 $F$ 位于 $x$ 轴正半轴，准线 $L$ 位于 $F$ 左侧，但仍在 $x$ 轴正半轴内。根据双曲线的参数关系，有：
\begin{equation} c = \sqrt{a^2 + b^2} = \frac{p e^2}{e^2 - 1}~. \end{equation}
与式 7 对比可知，$F$ 恰好是双曲线的一个焦点。此外，由于 $a = e |m - p| > |m - p|$，可以判断准线 $L$ 位于双曲线之外。

　　尽管在例 1 的推导时，要求 $e\neq1$。但对于式 4 ，当 $e = 1$ 时，有：

\begin{equation} y^2 = 2px - (2m - p)p~. \end{equation}

若令 $\displaystyle m = \frac{p}{2}$，即可得到抛物线的标准方程，正好与最初的要求相符。

　　由此可以看出，在 “焦点–准线” 定义的推导过程中，完全未涉及 “另一个焦点”。这一点恰好呼应了前文关于行星轨道的讨论：只需给定一个点和约束条件——焦点到准线的距离 $p$ 和距离比值 $e$，就能唯一确定一条圆锥曲线。其中，当 $e < 1$ 时对应椭圆，$e > 1$ 对应双曲线，而 $e = 1$ 则是抛物线。值得注意的是，所有的圆锥曲线的图像都与焦点位于准线的同一侧。

图 1：$p = 1$ 时，不同 $e$ 对应的结果

　　在之前的学习中，经常使用三个参数 $a, b, c$ 来描述椭圆或双曲线的性质。但无论是代数表达式中的 $a, b$，还是几何结构中的 $a, c$，本质上都只包含两个自由变量。事实上，这三个参数始终满足一个固定的约束关系，所以椭圆和双曲线只有两个自由度。这也从另一个角度说明，使用 $p$ 与 $e$ 作为定义参数是合理且充分的。

　　至此，终于验证了前面的猜想，得到了圆锥曲线的焦点–准线定义（Focus–Directrix Definition of Conic Sections）。

定义 1　圆锥曲线的焦点–准线定义

　　在平面上，给定一个定点 $F$ 和一条定直线 $L$，若 $F$ 不在 $L$ 上，则所有满足点到 $F$ 的距离与到 $L$ 的距离之比为某个固定常数 $e$ 的点 $P$ 的轨迹，称为圆锥曲线（conic section），即点 $P$ 满足：

\begin{equation} \frac{|PF|}{|PL|} = e,\quad(e>0)~. \end{equation}

其中，$F$ 称为圆锥曲线的焦点（focus），$L$ 称为圆锥曲线的准线（directrix），二者相互对应。焦点到准线的距离称为焦准距（focal parameter），通常记作 $p$；距离比值称为离心率（eccentricity），通常记作 $e$。

　　特别的：

当 $e = 0$ 时，轨迹为圆（circle）；
当 $0 < e < 1$ 时，轨迹为椭圆（ellipse）；
当 $e = 1$ 时，轨迹为抛物线（parabola）；
当 $e > 1$ 时，轨迹为双曲线（hyperbola）。

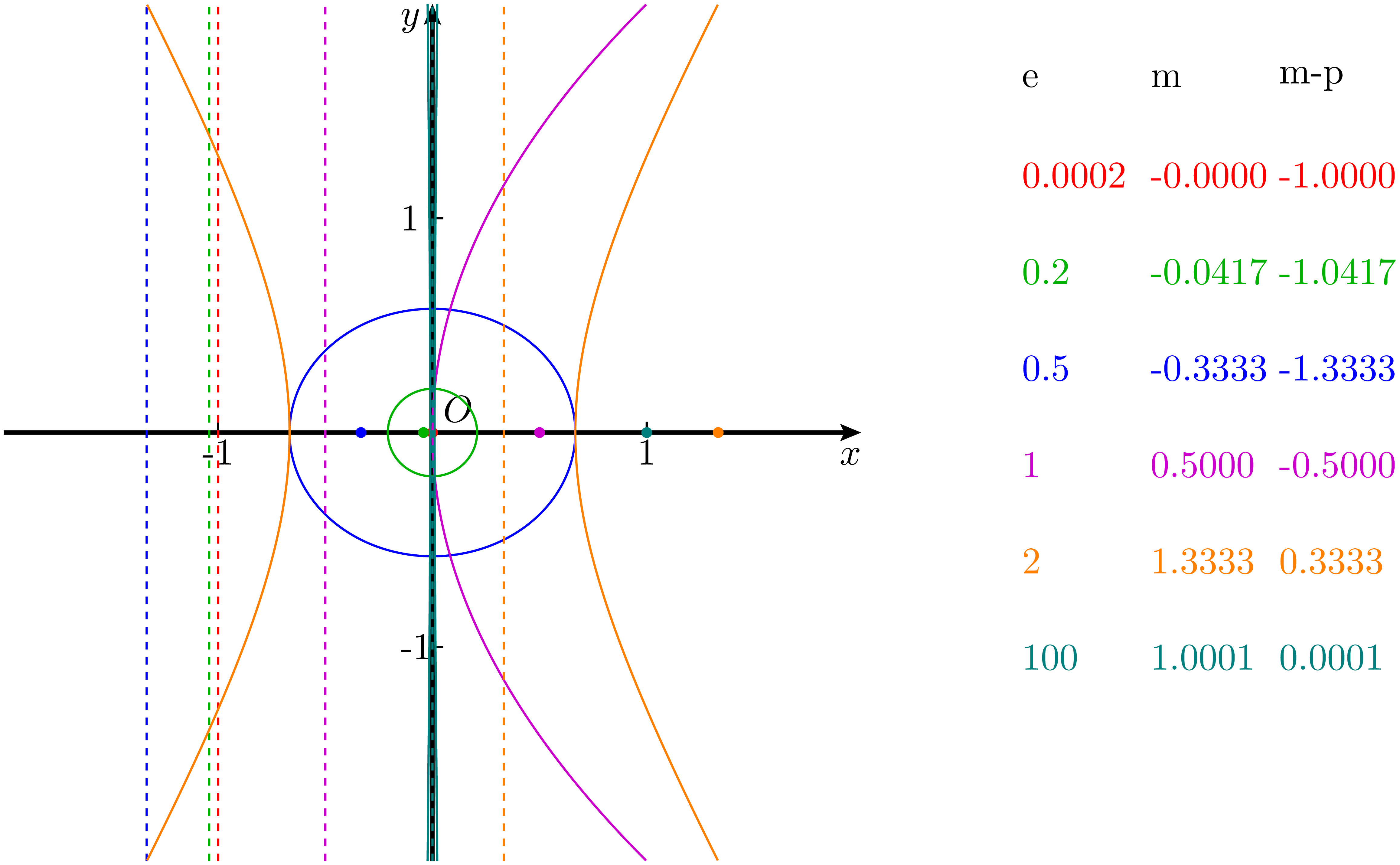
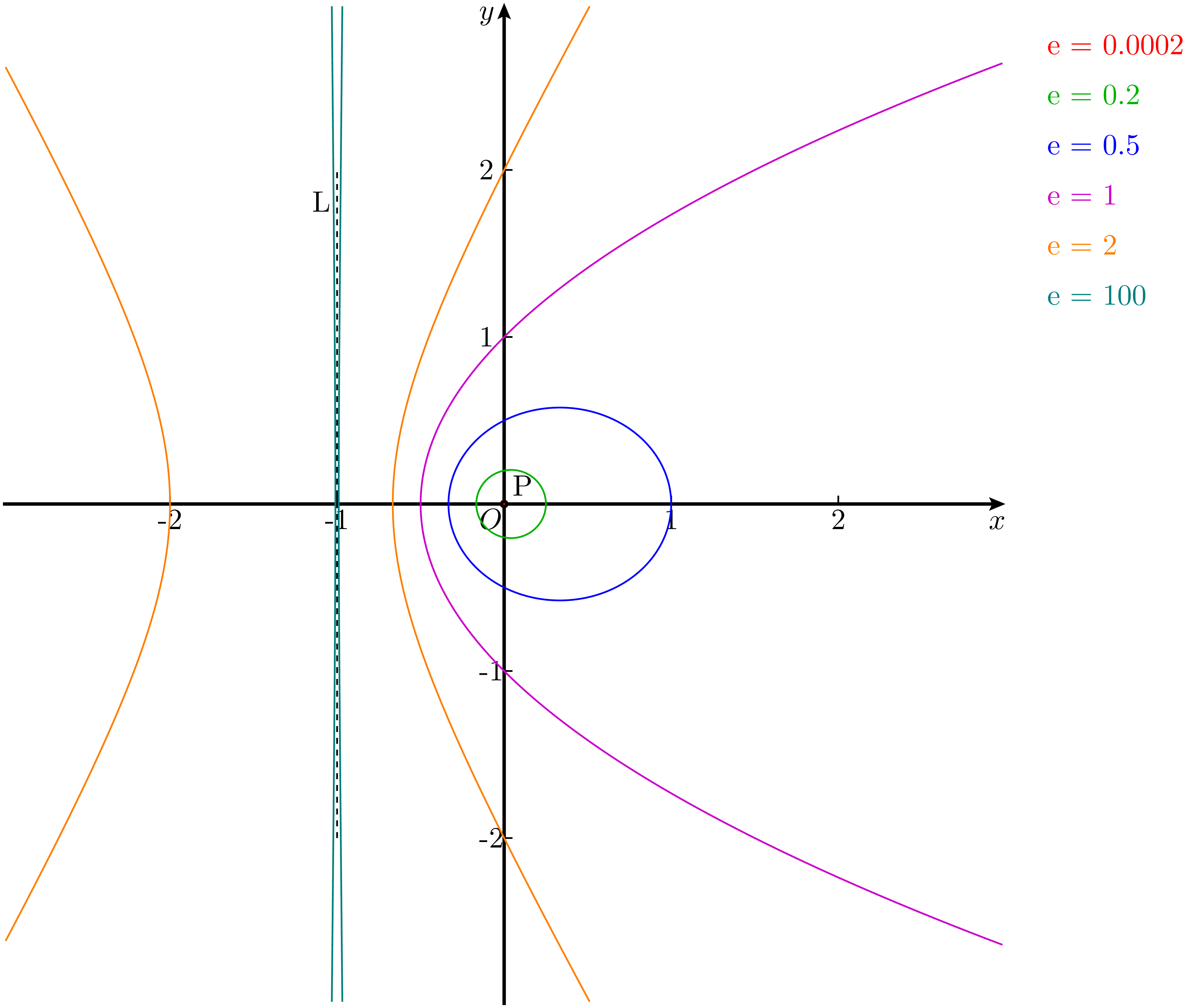
　　为了更清晰地进行对比，可以将图 1 中所有圆锥曲线的焦点和平移后的准线统一到相同的位置。图 2 中仍取 $p=1$，通过平移，使所有曲线的焦点位于原点 $(0,0)$，准线为 $x = -1$。这样更便于直观观察不同离心率 $e$ 下轨迹的差异。

图 2：$p=1$ 时，将所有焦点和准线平移到同一个位置上的对比

　　定义中，除了 $e = 0$ 所对应的情形，其他三种情况在前文中已有说明。在圆的定义中，只涉及一个圆心和一个半径。将统一定义中的焦点看作圆心并不难理解，毕竟在前面的推导中，其他圆锥曲线的焦点也是从圆心发展而来。而现在又给出了定义中的 $e = 0$，那么问题来了：准线去哪里了？而圆的半径，又该如何与焦准距建立联系？

　　解答这些问题，需要回到式 3 。当 $e = 0$ 时，有两种可能的情形：

第一种情况是分子为零，此时无论分母为何，等式恒成立，轨迹退化为定点 $F$ 自身。这与图 2 中原点处的红色轨迹所示的情况近似。
第二种情况是当 $p \to +\infty$，即分母趋于无穷大，若分子为有限常数 $r$，则根据极限计算，有 $\displaystyle\frac{r}{\infty} \to 0$，同样满足 $e = 0$。此时分子就对应圆的标准方程 $(x - m)^2 + y^2 = r^2$，定点 $F$ 为圆心，$p \to \infty$ 表示准线远离至无穷远处。由于图 2 中 $p$ 为有限值，不能直接显示这种情况，图中的绿色曲线近似反映了这种情况。

　　同理，当分母趋近于 $0$ 时，有 $e \to \infty$，此时轨迹趋近于准线本身，几乎退化为一条直线，而焦点看上去仿佛与 $(p, 0)$ 重合，这正对应图 2 中的青色情况。至于 “准线趋于无穷远” 或 “焦点趋于无穷远” 在几何上究竟意味着什么，则需要借助射影几何的视角才能更深入理解。不过，根据定义 1 ，现在有充分的理由这样说——所有圆锥曲线本质上是一类几何对象。

　　当然，例 1 的推导是基于给出定义之后的代数推导，直接根据定义也可以进行几何推导。设平面上有两个定点 $F_1, F_2$ 和两条定直线 $L_1, L_2$，其中每个定点与一条定直线一一对应。若 $L_1$ 与 $L_2$ 相互平行，且关于 $F_1F_2$ 的垂直平分线对称。若点 $P$ 满足：

\begin{equation} \frac{|PF_1|}{|PL_1|} = \frac{|PF_2|}{|PL_2|} = e~, \end{equation}

则点 $P$ 的轨迹是一条圆锥曲线。特别地，当 $|L_1L_2|>|F_1F_2|$ 时，在两线之间的轨迹为椭圆；当 $|L_1L_2|<|F_1F_2|$ 时，在两线之外的轨迹为双曲线。³

　　推导过程也不困难，根据式 16 ，当点 $P$ 在 $L_1,L_2$ 之间时，有：

\begin{equation} |PF_1|+|PF_2|=e(|PL_1|+|PL_2|)=e|L_1L_2|~. \end{equation}

由于 $e,|L_1L_2|$ 均为定值，此时 $P$ 点轨迹为椭圆，且根据圆锥曲线与焦点在准线同侧的约束关系有 $|L_1L_2|>|F_1F_2|$⁴。当点 $P$ 在 $L_1,L_2$ 之外时，有：

\begin{equation} ||PF_1|-|PF_2||=e||PL_1|-|PL_2||=e|L_1L_2|~. \end{equation}

由于 $e,|L_1L_2|$ 均为定值，此时 $P$ 点轨迹为双曲线，且根据圆锥曲线与焦点在准线同侧的约束关系有 $|L_1L_2|<|F_1F_2|$。根据这些推导，也可以得到准线的方程与圆锥曲线几何参数的关系。

3. 圆锥曲线的性质

　　之前研究椭圆等圆锥曲线时，在建立定义之后，通常会进一步分析它们各自的几何性质。而在前面已经建立了圆锥曲线的焦点–准线统一定义后，现在可以从一个统一的视角出发，探究它们所共有的一些几何特征。

　　首先，通过例 1 ，除了可以得到统一定义本身，进一步能够推导出以下结论：

对任意一条圆锥曲线，定点到定直线的垂线方向一定是该曲线的对称轴。
椭圆和双曲线，由于都具有两条对称轴，因此还可以沿另一条对称轴构造出第二组对应的焦点与准线。
圆的情况则更为特殊：由于具有无数条对称轴，可视作所有焦点都与圆心重合，并对应无数条准线。每条直径既然是圆的对称轴，那么自然也是焦点到准线的垂线方向。前文已提及，这些准线均位于无穷远处，且彼此重合，相关内容将在射影几何视角下的圆锥曲线中进一步说明。
从例 1 出发，还可以得到基于椭圆和双曲线的几何参数计算焦准距与离心率的表达式：
\begin{equation} \begin{split} p &= \left| \frac{a^2}{c} - c \right| = \frac{b^2}{c}\\ e &= \frac{c}{a}~. \end{split} \end{equation}
特别地，标准椭圆与双曲线的准线方程可根据焦点位于 $x$ 轴或 $y$ 轴的位置分别表示为：
\begin{equation} x = \pm\frac{a^2}{c} \qquad \text{或} \qquad y = \pm\frac{a^2}{c}~. \end{equation}

4. $e$ 和 $p$ 的性质

　　相信在观察图 2 时，读者已经能直观地感受到：随着 $e$ 的取值变化，曲线的具体形式也随之发生变化。从统一视角来看，$e$ 越小，曲线越 “闭合”，越接近圆；$e$ 越大，曲线越 “张开”，焦点越远离中心。从反射性质来看，随着 $e$ 增加，焦点处的反射光线由汇聚变为平行，再到发散，也形象地揭示了曲线张开程度的变化。

　　具体来看，对椭圆而言，无论如何 “张开”，其轨迹始终局限于抛物线的边界之内。因此，随着 $e$ 增大，椭圆只能愈发 “扁平”。而对双曲线来说，虽然其在焦点附近随 $e$ 增大而不断张开，但正如前文所述，它的一支在与抛物线相交之后，会逐渐收敛于自己的渐近线，永远不会超出抛物线的边界。因此，在圆锥曲线的统一模型中，抛物线恰好构成了椭圆与双曲线张开程度的 “临界极限”。

　　相比之下，参数 $p$ 主要决定曲线相对于焦点与准线的 “尺度” 大小，而不影响其类型。当 $e$ 固定时，改变 $p$ 会使图像整体放大或缩小，看上去好像曲线 “张开” 或 “收缩” 了，实则只是一次相似变换。换句话说，$p$ 的变化构成了以 $e$ 为分类基础的椭圆族、双曲线族或抛物线族。这一点，其实从 “所有抛物线构成一个族” 就能看出来——毕竟它本来也就只有 $p$ 这一个参数。而若固定 $p$，以 $e$ 为参数，则可以得到在某一尺度下的全部圆锥曲线族，这也正体现了统一定义的意义之一——通过一个表达式，整体把握不同圆锥曲线之间的变换关系。

　　总结一下，在平移和旋转下，$e$ 和 $p$ 都保持不变；而在相似变换（即整体放缩）下，$p$ 会改变，而 $e$ 保持不变。这揭示出二者的本质区别：$e$ 是一个纯粹的比例量，与尺度无关，因此具有更强的几何意义，适合用于分类；而 $p$ 则依赖度量单位，更适合描述具体图像的尺度与位置。事实上，$e$ 不仅在线性变换中保持不变，在仿射变换中也是不变的。

1. ^ 本站的前置内容，为免突兀，并未立即引入。
2. ^ 由于定义中的两个距离不再相等，直觉上不宜像抛物线那样，将点与准线对称地放在原点两侧。因此，这里先引入一个待定参数 $m$，后续再根据条件进行求解。抛物线的标准定义中相当于令 $\displaystyle m={p\over2}$。这是一种常见的处理方式。
3. ^ 其他条件下，轨迹可能会退化为一对关于两点连线对称的点或者不存在，读者可自行探究。
4. ^ 这一性质若尝试通过纯几何证明，难度较高；而若借助解析几何，则又回到了例 1 。因此，此处不再另作证明，而是直接依赖前面已得到的结论。