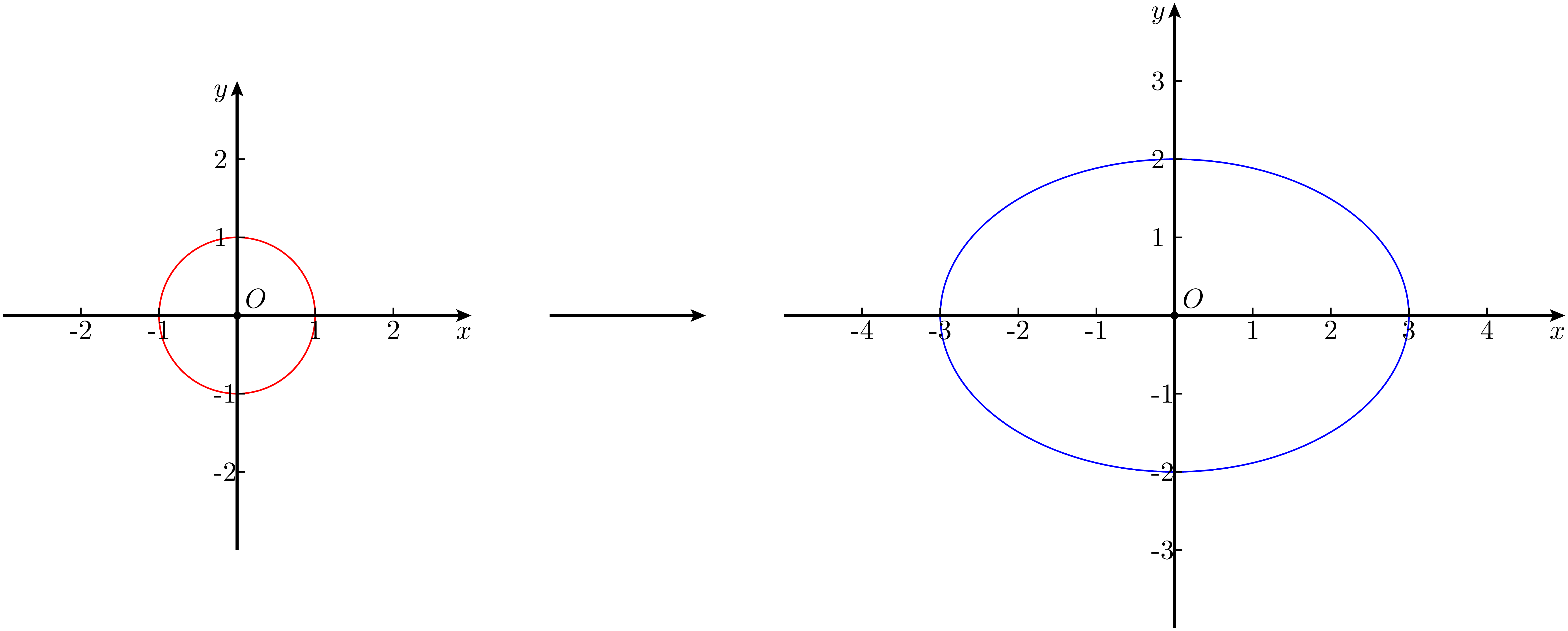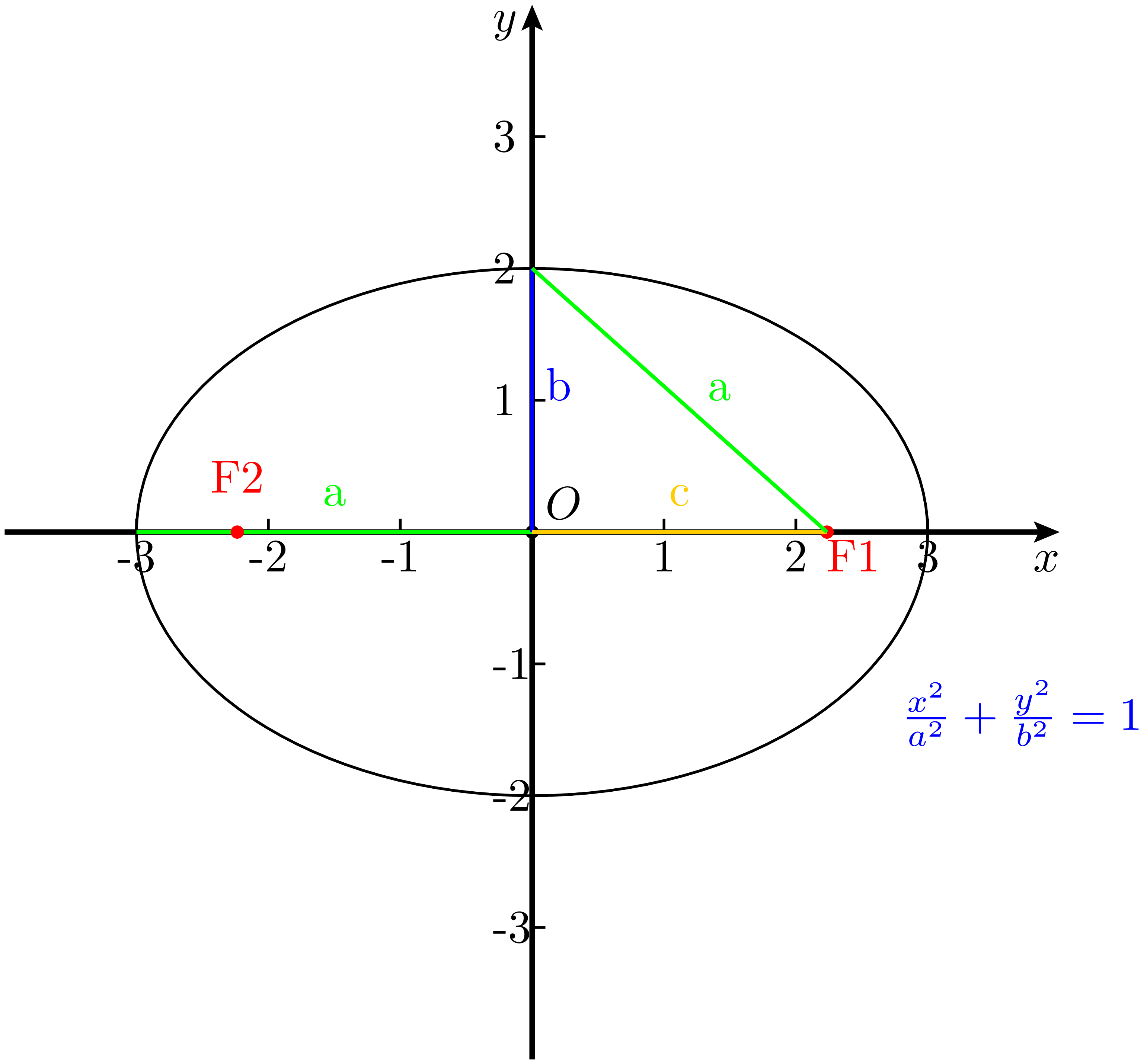椭圆（高中）

贡献者：欄、停敘; addis

预备知识　解析几何，圆，函数的变换

　　人们常说地球绕着太阳转。提到 “绕着转”，很多人会自然联想到一个完美的圆形轨道。但实际上，真正沿正圆轨道运行的行星几乎不存在。大多数行星的轨道虽然是封闭的环绕，但略微 “压扁”，并不是严格的圆形。类似这种 “被压扁的圆” 在生活中也很常见，比如一个圆形水杯的杯口，在斜着观察时，所看到的轮廓就是这种形状。

　　有一种被称为 “回声墙” 的特殊建筑设计：只要两个人分别站在弧形墙上的两个特定位置，即使中间隔着整面墙，也能清晰地听到彼此的低语。研究发现，这种现象的产生依赖于墙体的形状满足一种特殊的曲线条件——从一个点发出的声音或光线，经过曲线表面的反射后，总能精准地传到另一个固定点。

　　令人惊讶的是，这两种现象中出现的曲线，实际上是同一种。接下来，将从这两个视角分别出发，一步步探索这种曲线的几何特性。在研究各自的方程之后，进一步验证它们对应的是同一个图形，并由此引出椭圆的定义、标准方程和基本参数，逐步来认识这个优雅而又实用的几何对象。

1. “压扁的圆”

　　先来研究水杯杯口那种略微压扁的圆形轮廓。下面将从单位圆出发，只从几何变化的角度入手，研究其经过轴向放缩后所形成的形状，暂且称其为 “压扁的圆”。

　　具体地，单位圆的方程为：

\begin{equation} x^2 + y^2 = 1~. \end{equation}

其与 $x$ 轴的交点为 $(1, 0), (-1, 0)$，与 $y$ 轴的交点为 $(0, 1), (0, -1)$，分别确定了单位圆的两个直径，当然也是单位圆的两个对称轴。考虑将单位圆在 $x$ 轴和 $y$ 轴方向分别拉伸 $p$ 倍和 $q$ 倍（其中 $p, q$ 为任意正数）。根据图像变换的规律，若在 $x$ 或 $y$ 方向进行 $k$ 倍拉伸，对应变量将变为原来的 $\displaystyle\frac{1}{k}$。因此，拉伸后的曲线方程为：

\begin{equation} \left(\frac{x}{p}\right)^2 + \left(\frac{y}{q}\right)^2 = 1\implies\frac{x^2}{p^2} + \frac{y^2}{q^2} = 1~. \end{equation}

　　根据图像变换的结果，曲线在 $x$ 轴上的交点为 $(p, 0), (-p, 0)$，在 $y$ 轴上的交点为 $(0, q), (0, -q)$，它们限制了图像在两个方向上的最大范围。这四个交点被称为顶点（vertex），它们确定的两条线段，尽管不再是直径，但显然根据变化的过程，它们是图像的唯二的对称轴，两条线段长度分别为 $2p$ 和 $2q$。圆心仍然是整个图形的对称中心，在这里也就是 $(0,0)$。

图 1：从圆到“压扁的圆”

　　其实，如果考虑平移或旋转规律，还可以得到这个 “压扁的圆” 在任意位置或对称轴指向任意方向时的情况，下面给出伸缩后再平移得到的，对称中心在 $(x_0,y_0)$ 处的曲线方程，感兴趣可以根据规律推导：

\begin{equation} \frac{(x-x_0)^2}{p^2} + \frac{(y-y_0)^2}{q^2} = 1~. \end{equation}

　　在高中阶段，这里只研究对称中心在原点处的曲线，也即式 2 。参考圆的 “直径” 和 “半径”，通常，将 $p, q$ 中较大的一个对应的对称轴或其长度称为长轴（major axis），记作 $2a$，其中 $a$ 称为半长轴（semi-major axis）；较小的一个对应的对称轴或其长度为短轴（minor axis），记作 $2b$，其中 $b$ 称为半短轴（semi-minor axis）。二者始终满足 $a>b>0$，即：

$p>q$ 时，长轴在 $x$ 轴上，短轴在 $y$ 轴上，曲线方程为：
\begin{equation} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1,\qquad(a>b>0)~. \end{equation}
$p< q$ 时，长轴在 $y$ 轴上，短轴在 $x$ 轴上，曲线方程为：
\begin{equation} \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1,\qquad(a>b>0)~. \end{equation}

　　注意，这里的 $a,b$ 是任意给出的，二者没有约束，也就是说每任意给出一对 $(a,b)$ 就能确定两个这种 “压扁的圆”，他们的形状完全相同，只是旋转了 $90^\circ$。

2. 椭圆的几何定义

　　下面尝试从圆的定义出发，探索其推广的可能性。圆通常被定义为：到某个定点（圆心）的距离为定值的所有点的轨迹。这个定义由三个要素构成：一个定点 $O$、一种距离关系 $|OP|$ 和一个固定的数值 $r$。若希望推广这一定义，就需要在这三者中动些手脚。

　　受割线趋近于切线的启发，可以从 “定点” 的结构入手。设想将圆心视为两个重合在一起的点 $O_1,O_2$，此时圆上的每个点到这两个点的距离 $|O_1P|,|O_2P|$ 都相等，且为同一个定值 $|O_1P|=|O_2P|=r$。现在，将这两个点轻微分开，保持 $|O_1P|=|O_2P|$ 这一条件不变，而打开他们为定值的前提，考察所有到这两个点距离相等的平面点集合，会发现所得图形是一条连接这两点的线段的垂直平分线。这早在初中阶段就学过，甚至用尺规作图时，就是从两个定点分别作等半径的圆，圆的交点连线便是这两个点的垂直平分线。

　　这启发人们进一步思考：$|O_1P|=|O_2P|=r$ 能不能构造成其他的表达方式，前面的构造是打开了第二个等号，如果打开第一个等号，那么会发生什么？也就是说，将 $|O_1P| = r, |O_2P| = r$ 作为一种初始设定，而不要求它们始终相等。一种比较自然的推广方式是考虑两者的和保持为定值，即 $|O_1P| + |O_2P| = 2r$，这意味着这两个距离始终满足一个固定的和 $m$¹。下面试着推导一下他的表达式。

例 1　对两定点 $F_1(c, 0)$ 和 $F_2(-c, 0),(c>0)$，若点 $P$ 满足 $|PF_1| + |PF_2| = m,(m > 2c)$，求 $P$ 方程。

　　解：

　　设点 $P$ 坐标为 $(x, y)$，根据题意有：

\begin{equation} \sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = m~. \end{equation}

移项后，两边平方有：

\begin{equation} (x + c)^2 + y^2 = m^2 - 2m\sqrt{(x - c)^2 + y^2} + (x - c)^2 + y^2~. \end{equation}

打开整理有：

\begin{equation} 2m\sqrt{(x - c)^2 + y^2}= m^2 - 4cx~. \end{equation}

两边平方，打开有：

\begin{equation} 4m^2(x^2 - 2cx+c^2) + 4m^2y^2= m^4-4m^2\cdot2cx+16c^2x^2~. \end{equation}

整理后得到：

\begin{equation} 4(m^2 -4c^2)x^2 + 4m^2y^2= m^2(m^2-4c^2)~. \end{equation}

两侧同时除以 $(m^2-4c^2)m^2$ 后得到：

\begin{equation} \frac{x^2}{\left(\displaystyle\frac{m}{2}\right)^2} + \frac{y^2}{\displaystyle\left(\frac{m}{2}\right)^2-c^2}=1~. \end{equation}

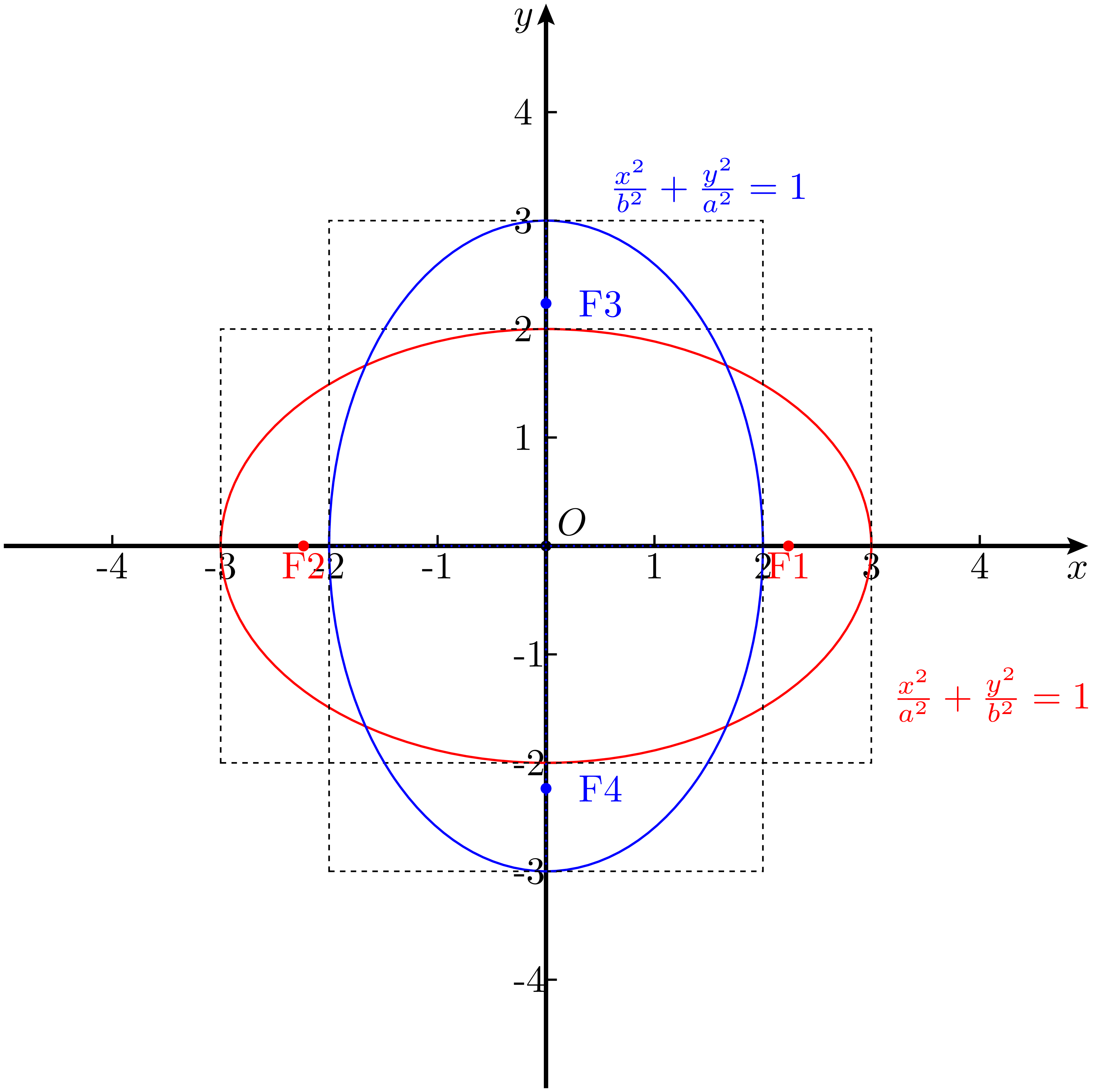
　　由于 $m>2c>0$，也就是 $\displaystyle\left(\frac{m}{2}\right)^2-c^2>0$，可以看出，例 1 的结果的形式与式 2 相同，也就是说二者的结果对应着同一个形状，就称其为椭圆（ellipse）。同理易知，如果两个定点分别为 $F_1(0,-c)$ 和 $F_2(0,c),(c>0)$，则相当于更换 $x,y$ 的结果位置，得到的表达式是：

\begin{equation} \frac{x^2}{\displaystyle\left(\frac{m}{2}\right)^2-c^2}+\frac{y^2}{\left(\displaystyle\frac{m}{2}\right)^2} =1~. \end{equation}

　　令式 11 和式 4 、式 12 和式 5 对应相等，可以发现，总有：

\begin{equation} \left(\frac{m}{2}\right)^2=a^2,\qquad \left(\frac{m}{2}\right)^2-c^2=b^2~. \end{equation}

整理之后有：

\begin{equation} m=2a,\qquad a^2=b^2+c^2~. \end{equation}

　　到这里，综合前面的推导可以得到椭圆是到两个定点距离之和为定值的点的集合，这个定值等于椭圆的长轴长。这也就得到了椭圆的几何定义，也称为椭圆的第一定义。

定义 1　椭圆的几何定义

　　在平面上，所有满足到两个定点 $F_1$ 与 $F_2$ 的距离之和为常数 $2a$ 的点 $P$ 的轨迹，构成一个几何图形，称为椭圆（ellipse）。即，对于椭圆上的任意一点 $P$，都有：

\begin{equation} |PF_1| + |PF_2| = 2a ,\qquad(2a>|F_1F_2|)~. \end{equation}

其中，$F_1$ 和 $F_2$ 被称为椭圆的两个焦点（focus），两焦点之间的距离 $|F_1F_2|$ 称为椭圆的焦距（focal distance），记作 $2c$，其中 $c$ 被称为半焦距（semi-focal distance），也称为椭圆的线性离心率（linear eccentricity）。

　　可以看出，椭圆的定义中给出的参数是 $(a,c)$，与之前任意给出 $(a,b)$ 类似。值得注意的是，如果同时给出 $(a,b,c)$ 三个参数，则它们必须得满足 $a^2+b^2=c^2$ 才能确定一个椭圆。或者说，当任意给定一组 $(a,b)$ 或 $(a,c)$ 时，第三个参数就唯一确定了，也就是说对给定范围的椭圆，他的焦点位置是唯一确定的，而给定了长轴和焦距，则短轴也唯一确定了。

　　式 14 是椭圆非常重要的一个基本性质，$a,b,c$ 三者的关系正好可以构成一个直角三角形。而恰巧，在椭圆内半焦距与半短轴永远是垂直的，因此将半短轴的端点与焦点连起来构成的直角三角形的斜边长恰好就是半长轴。

图 2：$a,b,c$ 关系

　　特别地，根据之前推导过程的思路，当一个椭圆的两个焦点重合，即 $c=0$ 时，椭圆就变成了圆。根据三者的关系，也可以得到 $a=b$，也印证了这一点。所以可以这样说，圆是椭圆的一个特例。

3. 椭圆的方程

　　式 4 、式 5 合称为椭圆的标准方程。

定理 1　椭圆的标准方程

长轴在 $x$ 轴上，短轴在 $y$ 轴上的椭圆方程为：
\begin{equation} \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1,\qquad(a>b>0)~. \end{equation}
长轴在 $y$ 轴上，短轴在 $x$ 轴上的椭圆方程为：
\begin{equation} \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1,\qquad(a>b>0)~. \end{equation}

图 3：标准椭圆

　　就像圆的标准方程、直线的方程那样，只要得到的表达式符合标准方程的形式，那么就可以确定其图像为椭圆。另外，类似于圆的参数方程那样，利用三角恒等式 $\sin^2x+\cos^2x=1$，可以伸缩变形得到椭圆的参数方程。

定理 2　椭圆的参数方程

\begin{equation} \begin{cases} x(\theta) = p\cos \theta\\ y(\theta) = q\sin \theta \end{cases},\quad \theta \in [0, 2\pi) ~. \end{equation}

　　注意，这里与式 2 一样，$p,q$ 中更大的那个是半长轴，另一个是半短轴。

椭圆族

　　这里引入一个新的概念，称为族（family）。他是解析几何里面很重要的概念，由一个或多个参数连续变化所生成的一组对象，就称为一个族。下面以椭圆为例来感受一下。

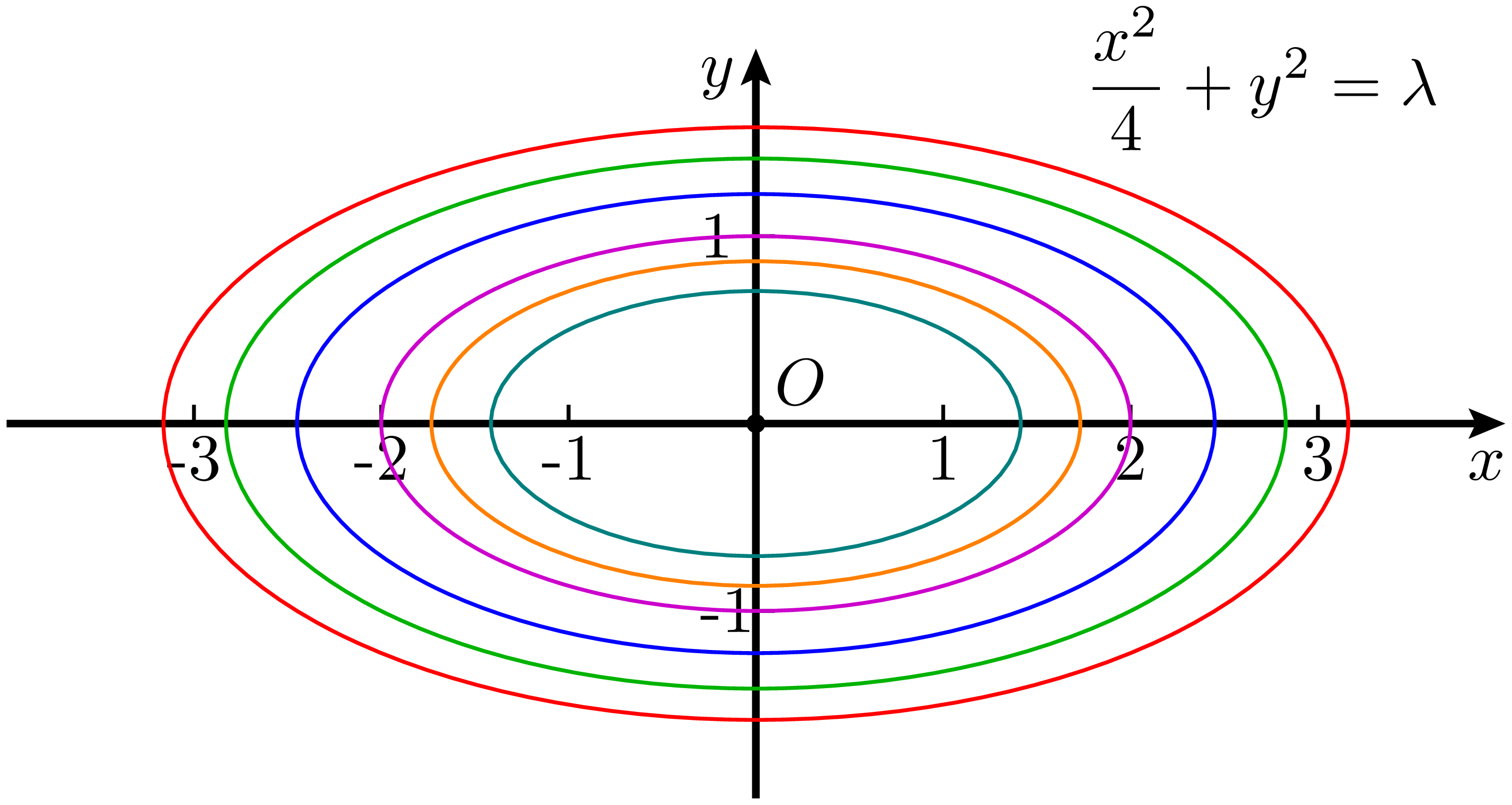
　　通过对椭圆标准方程的代换，可以构造出一个椭圆族。设取 $a = \sqrt{\lambda} p,b = \sqrt{\lambda} q$，其中 $\lambda >0$。以式 16 为例，代入后可得：

\begin{equation} \frac{x^2}{\lambda p^2} + \frac{y^2}{\lambda q^2} = 1,\qquad(p>q>0)~. \end{equation}

　　这个方程仍符合椭圆的标准形式，因此它的形状仍应该是椭圆，只是其中出现了一个未确定的参数 $\lambda$。也就是说，每给出一个符合条件的 $\lambda$ 的值就可以得到一个椭圆。稍作整理，可以得到：

\begin{equation} \frac{x^2}{p^2} + \frac{y^2}{q^2} = \lambda,\qquad(p>q>0)~. \end{equation}

这看起来与标准椭圆方程略有不同，相当于将等号右边的 $1$ 替换成了一个参数 $\lambda$。

　　实际上，前面的代换也可以理解为取 $x = \sqrt{\lambda} x',y = \sqrt{\lambda} y'$（$\lambda>0$）得到的结果。根据图像变换的规律，这相当于在 $x$ 和 $y$ 两个方向上进行了等比例的缩放，就像同心圆的扩展一样。

　　例如，设 $p = 2,q = 1$，则表达式为 $\displaystyle\frac{x^2}{4} + y^2 = \lambda$。如果取 $\lambda = 0.5, 0.75, 1, 1.5, 2, 2.5$，就可以画出从内到外一系列大小不同但形状相似的椭圆，如图 4 所示。

图 4：椭圆族 $\displaystyle\frac{x^2}{4} + y^2 = \lambda,(\lambda>0)$

　　这样通过引入参数 $\lambda$，就可以用一个方程式统一表示一族具有相似性质²的椭圆，这在解决某些问题时可以大大简化思考和计算过程。

4. 椭圆的性质

　　前面分别从两个圆的变形的视角和焦点从圆心分开的视角从圆得到了椭圆。这两个视角分别从圆迁移了一些性质到椭圆身上。

椭圆的反射性质

定理 3　椭圆反射性质

　　对于一个椭圆，其两个焦点为 $F_1$ 和 $F_2$。对椭圆上的任意一点 $P$，如果从 $F_1$ 发出一条光线射向 $P$，并在 $P$ 点发生镜面反射，那么反射光线将经过 $F_2$。也就是说直线 $PF_1$ 与 $PF_2$ 关于切线 $l$ 对称，即：

\begin{equation} \angle (F_1P, l) = \angle (F_2P, l)~. \end{equation}

其中 $l$ 是椭圆在点 $P$ 处的切线，或

\begin{equation} \angle (F_1P, n) = \angle (F_2P, n)~. \end{equation}

其中 $n$ 是点 $P$ 处反射的法线。

　　在最初讲述 “回声墙” 现象时，已经提及了椭圆的这一特性。但与子节 1 中的直观例子不同，子节 2 在推导椭圆的几何定义时，并未直接从该现象出发。下面对原因作一下说明。

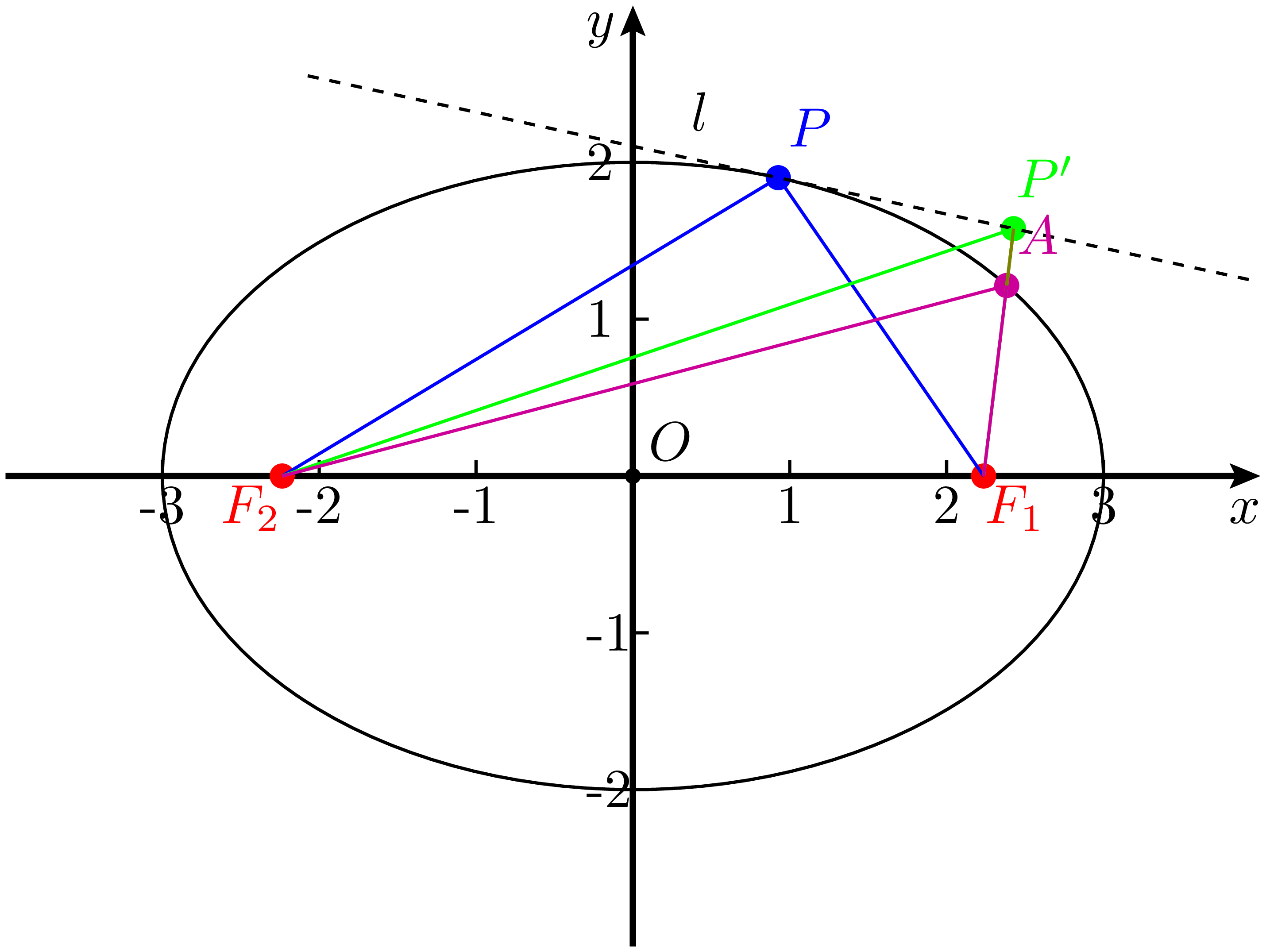
　　设平面上有两个定点 $M,N$，以及两点同侧的一条直线 $l$。若要求从直线上某点出发，依次经过 $M$ 和 $N$ 的路径总长度最短，即寻找一条满足 $PM + PN$ 最小的路径。这是初中阶段就学过的 “将军饮马” 问题。其几何解法是：先作点 $M$ 关于直线 $l$ 的对称点 $M'$，再连接 $NM'$，则连接线与直线 $l$ 的交点 $P$ 即为所求路径上的点。此时，线段 $PM$ 与 $PN$ 关于直线 $l$ 对称，或者说，两者与直线 $l$ 所成的夹角相等。这正好对应了物理中 “反射” 的概念。

　　构建 “回声墙” 时，实际的问题是：希望找到所有从 $M$ 出发，经直线反射后到达 $N$ 且总路程相等的路径，即 $MP + PN$ 为定值。由于直接找出所有符合反射条件的路径较困难，反过来，先考虑平面上满足 $|MP'| + |NP'| = |MP| + |NP|$ 的所有点 $P'$，即满足两段路径长度之和不变的点集，然后再从中筛选符合反射条件的。第一步得到的正是一个椭圆。而令人惊奇的是，椭圆上的每一个点不仅满足总路程为定值的条件，还都符合反射规律。因此，在子节 2 中，直接从 “距离之和为常数” 的几何定义出发，就足以推导出椭圆。

图 5：证明反射性质

　　这个性质的证明也不难，如图 5 对于椭圆上任意一点 $P$，在 $P$ 处的切线 $l$ 上任取 $P$ 外一点 $P'$。则对于椭圆的两个焦点 $F_1,F_2$，连接 $PF_1,PF_2,P'F_1,P'F_2$，则由于 $l$ 是切线，$P'F_1$ 必与椭圆相交于一点，记作 $A$，连接 $AF_2$，则在三角形 $P'AF_2$ 中，根据三角形不等式有 $|AF_2|<|AP'|+|P'F_2|$，从而有：

\begin{equation} |P'F_1|+|P'F_2|=|P'A|+|AF_1|+|P'F_2|>|AF_1|+|AF_2|=|PF_1|+|PF_2|~. \end{equation}

根据 $P'$ 的任意性，$P$ 是 $l$ 上与二者连线最小的点，根据之前 “将军饮马” 问题的结论，点 $P$ 处即发生了 “反射”。而由于 $P$ 的任意性，椭圆上的所有点都满足这个性质。

与圆类似的性质

　　椭圆具有关于长轴与短轴的对称性，且这两条轴是椭圆仅有的两个对称轴。此外，椭圆还关于其几何中心呈中心对称。在标准形式的椭圆中，根据平方项可以容易地看到它的对称性，此时椭圆的对称轴分别是 $x$ 轴和 $y$ 轴，而椭圆的中心正是坐标原点 $(0,0)$，椭圆上点的取值范围³为 $x\in[-a,a],y\in[-b,b]$，也就是说，椭圆被限定在一个长为 $2a$，宽为 $2b$ 的矩形内部。

　　参考圆的面积为 $S = \pi r^2$，以及半径对应半长轴和半短轴。从椭圆是圆的伸缩的视角，一个大胆的猜想是，椭圆的面积满足：

\begin{equation} S = \pi a b~. \end{equation}

好消息是这个猜想是成立的，但是其证明需要使用定积分，此处不予赘述。

　　另外，参考圆的直径所对圆周角始终为直角，也即直径两端点与圆上其他任意点的连线，斜率之积为 $-1$。与圆类似，设过原点的某条直线与椭圆交于 $A,B$ 两点，点 $M$ 是椭圆上异于 $A,B$ 的动点，若 $MA,MB$ 的斜率存在为 $k_{MA},k_{MB}$，则 $k_{MA}\cdot k_{MB}$ 定值：

\begin{equation} k_{MA} \cdot k_{MB} = -\frac{b^2}{a^2}~. \end{equation}

这个性质可以利用解析几何的方法联立求解。特别地，如果圆是取 $a=b$ 的情况，与这里也相同。

切线

　　根据介绍过的隐函数求导法，容易得到椭圆作为隐函数的导数为：

\begin{equation} \frac{2x}{a^2} + \frac{2yy'}{b^2} = 0~. \end{equation}

即椭圆上某点 $(x_0,y_0)$ 处，切线斜率为 $\displaystyle-\frac{b^2}{a^2}\frac{x_0}{y_0}$，这也可以通过连立直线与椭圆的方程，然后按照只有一个交点的方法得到。有了斜率之后，也可以采用解析几何的方法来验证椭圆的反射性质。

　　另外，根据点斜式，可以整理得到椭圆的切线方程为：

\begin{equation} \frac{xx_0}{a^2} + \frac{yy_0}{b^2} = 1~. \end{equation}

这个形式很有规律，就像是在椭圆的方程中，把一个 $x$ 和一个 $y$ 分别替换成了椭圆上某个固定点的坐标 $(x_0, y_0)$，就能直接写出该点处的切线方程。

椭圆的弦

　　类似于圆中 “弦” 的概念，椭圆中也可以定义弦：一条穿过椭圆内部某点的直线与椭圆相交于两点，连接这两点的线段称为椭圆的弦（chord）。椭圆的任意一条弦，其长度 $s$ 总满足 $s\leq2a$，而长轴是椭圆中唯一最长的弦⁴。

图 6：长轴是最长的弦

　　设以 $a$ 为半径分作同心圆 $O$，即圆心与椭圆重合。在图中可以发现，椭圆的除长轴外的所有弦在延长后均与圆 $O$ 相交，意味着这些弦是圆 $O$ 弦的一部分。而因为圆 $O$ 的任何一条弦长度都不超过其直径 $2a$，因此可以得到弦长的上限与长轴的唯一性。

　　若一条弦通过椭圆的焦点，则称该弦为焦点弦（focal chord）。在所有焦点弦中，只有长轴同时通过两个焦点。垂直于长轴的焦点弦被称为通径（latus rectum），它是最短的焦点弦。通径的长度固定为：

\begin{equation} L = \frac{2b^2}{a}~. \end{equation}

　　此外，椭圆中还有一个与圆类似的概念，称为焦半径（focal radius），即从焦点到椭圆上一点的连线。一条焦点弦也可以看作是由两条焦半径所组成。

1. ^ 当然，也可以要求两者的乘积是一个定值 $m$，即 $|O_1P||O_2P| = m$，此时得到的图形称为卡西尼曲线（Cassini curve）。
2. ^ 这个相似的性质就是它们的离心率相同。
3. ^ 假设长轴在 $x$ 轴。
4. ^ 注意短轴并非最短的弦。