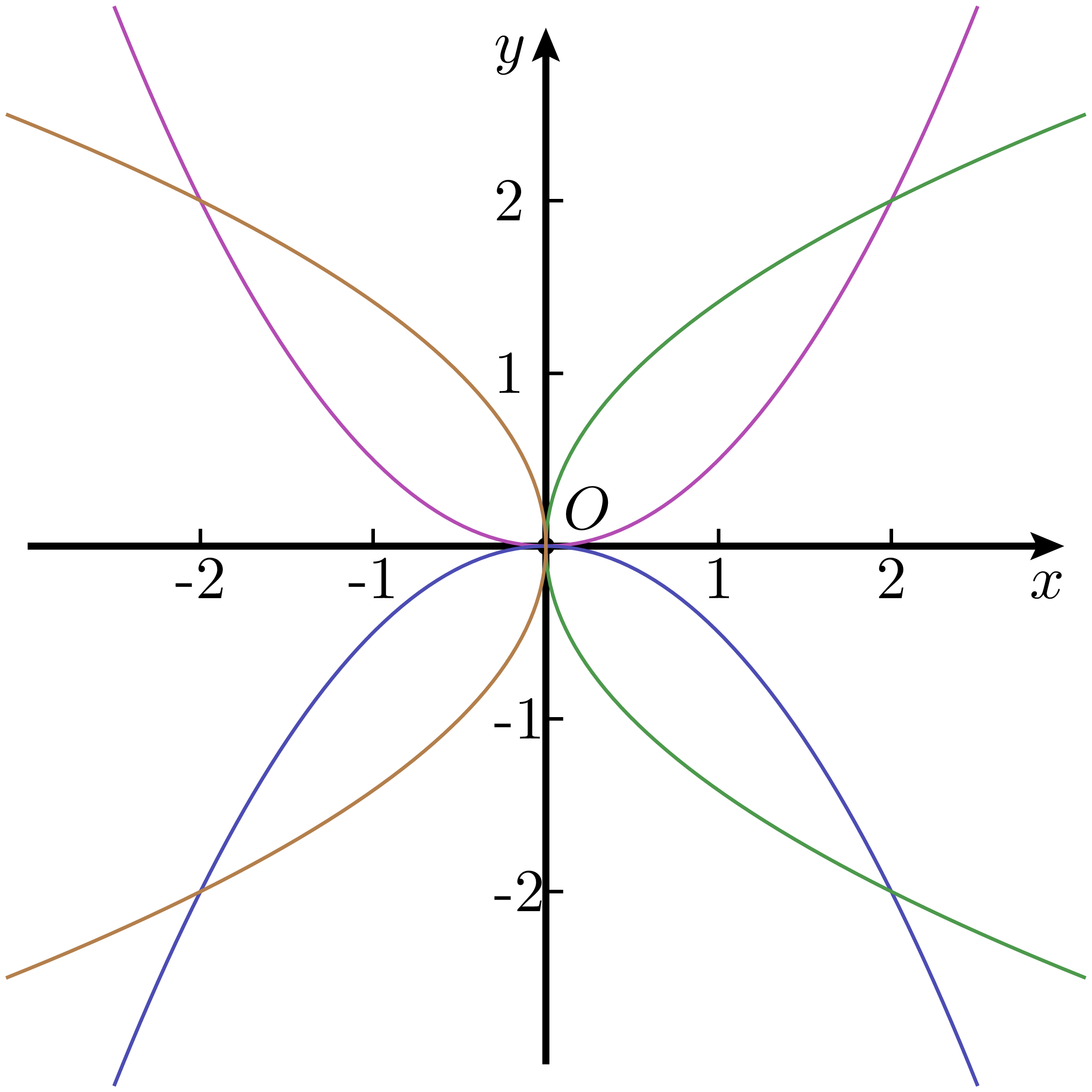抛物线（高中）

                     

贡献者： 欄、停敘; addis; ACertainUser

预备知识　解析几何，圆，双曲线，点到直线的距离

　　 不知道读者在初次接触双曲线时，是否产生了一种似曾相识的感觉：它的一支看起来与初中阶段学习过的二次函数图像——“抛物线” 非常相似：两者都不封闭，都有一个开口，形状略微弯曲，并向无限延伸，甚至同样具有对称轴。相信一些读者可能早已不禁在心中将双曲线的一支看成抛物线，认为双曲线不过是 “两个抛物线” 的组合而已。

　　 这种误解并不罕见。抛物线和双曲线在图像上确实有相似之处，但它们在几何定义、解析式结构以及性质等方面有着明显的差别。之所以容易混淆，很大程度上与初中学习的重点有关。那时更注重的是二次函数的代数表达与图像之间的关系，例如开口方向、对称轴、顶点坐标和零点等。这些内容有助于建立对抛物线的基本印象，但主要停留在函数视角，对抛物线作为几何图形本身的理解较为有限。

　　 大多数人对抛物线的印象，往往停留在现实生活中物体被抛出后所形成的轨迹。在理想状态下，这类轨迹正是一条抛物线，这也正是 “抛物线” 名称的来源。然而，随着人们的进一步研究发现，抛物线并不仅仅出现在物理运动中，它还具有独特的几何性质，在许多实际工程中发挥着重要作用。例如，雷达天线的反射面通常设计成抛物面结构，原因就在于抛物线具备一种精确的聚焦特性：来自远处的平行电磁波在抛物面上反射后，会准确地汇聚到焦点；而从焦点出发的信号，也能被反射成方向一致的平行波。这一聚焦能力，使抛物面非常适合实现能量的集中与传输，使抛物线广泛出现于雷达、卫星通信设备、汽车大灯以及太阳能灶等场景中。

1. 抛物线的定义

　　 由于初中阶段已经花了很多力气研究二次函数，并且基本了解了抛物线的图像特征，因此此处不再从函数的角度展开，而是直接进入定义的探讨。

　　 在研究椭圆和双曲线的过程中，曾尝试将圆的定义加以推广。圆可以看作是满足条件 $|O_1P| = |O_2P| = r$ 的点 $P$ 的集合，其中 $O_1$ 与 $O_2$ 是重合的点，二者之间的距离 $d(O_1,O_2)=0$。如果放宽这个限制，即允许 $d(O_1,O_2)$ 不为零，并且打开第一个等号，就可以得到椭圆和双曲线这两种新曲线，这在之前已经探究过了。那么，如果不打开第一个等号，而是改为将第二个等号 “打开”，只要求 $|O_1P| = |O_2P|$ 呢？之前提到过，在这种设定下，点 $P$ 的轨迹就是所有到两个定点距离相等的点——也就是这两点连线的垂直平分线。看起来，这样的修改似乎已经没有什么进一步变化的空间了。1不过，不妨换个思路。既然要求的是两个距离相等，而之前学过的 “距离” 可以是两点之间的距离、两条平行线之间的距离，或者点到直线的距离，那有没有可能试着改变一下条件中的几何元素呢？

　　 比如，如果换成两条平行线，那和原来的情况本质上差别不大，轨迹仍然是两条线段之间的一条平行直线。那如果保留其中一个点 $O_1$，把另一个点 $O_2$ 替换为一条固定的直线 $l$2，问题就变成了：所有满足 “到某个固定点和某条固定直线的距离相等” 的点 $P$，它们的轨迹会是什么样的图形？

　　 当然，这样修改之后还需要修改 $d$，否则如果直线 $l$ 正好通过定点 $O_1$，唯一满足条件的点就只有 $O_1$，轨迹会退化成一个点。当令 $d$ 满足 $d(O_1,l)=p,(p\neq0)$ 时，情况就变得有趣起来。

例 1　对定点 $F\left(0, \displaystyle\frac{p}{2}\right)$ 和 $l:y=-\displaystyle\frac{p}{2},\left(p>0\right)$，若点 $P$ 满足 $|PF|=d(P,l)$，求点 $P$ 的轨迹方程。

　　 解：

　　 设点 $P$ 的坐标为 $(x, y)$，题设条件表示点 $P$ 到定点 $F$ 的距离等于它到直线 $l$ 的距离。写成数学表达式为：

\begin{equation} \sqrt{x^2 + \left(y - \frac{p}{2}\right)^2} = |y + \frac{p}{2}|~. \end{equation}

　　 两边平方后，展开并整理，利用平方差公式，有：

\begin{equation} x^2 = \left(y + \frac{p}{2}\right)^2 - \left(y - \frac{p}{2}\right)^2 = 2py~. \end{equation}

图
图 1：例 1

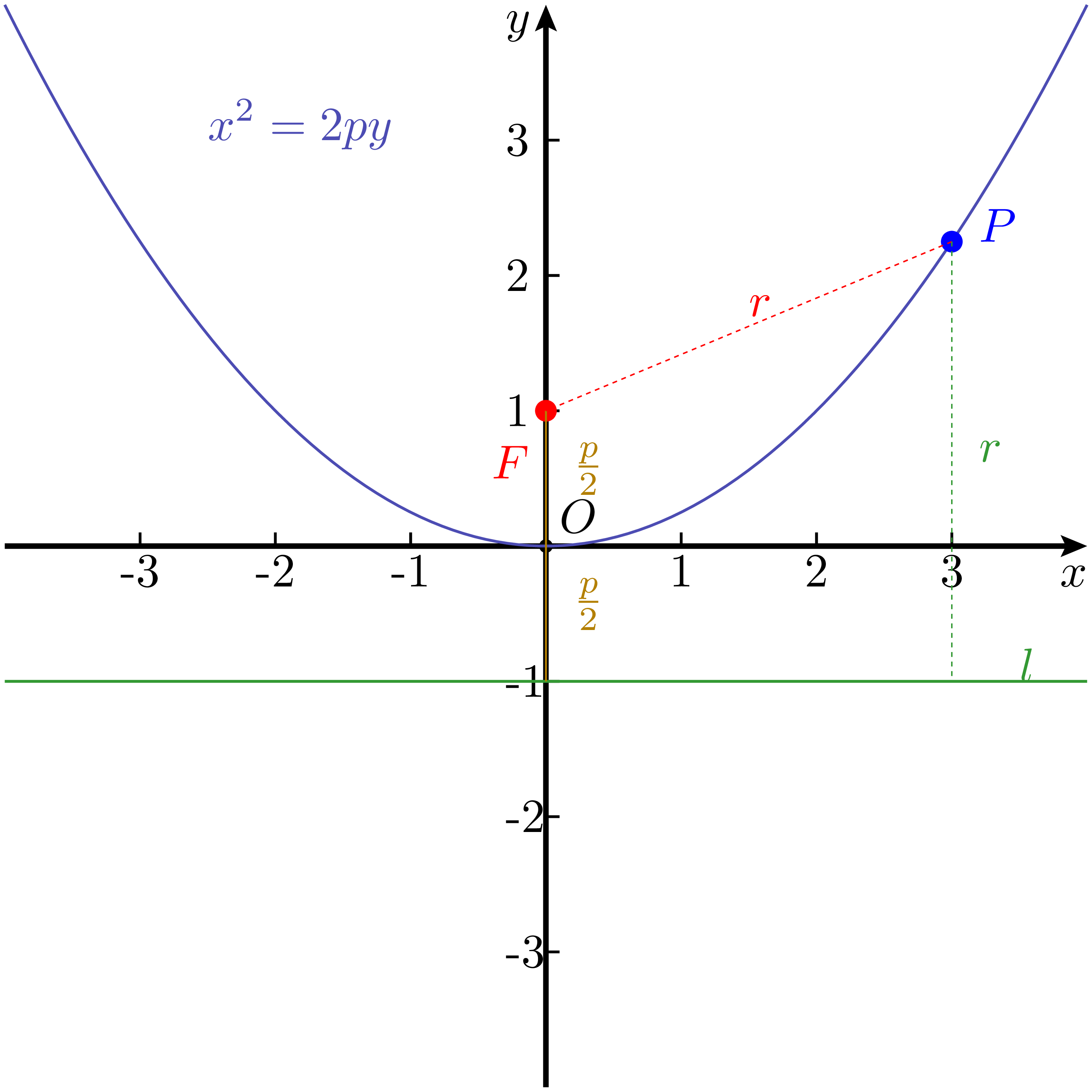
　　 可以注意到，原点正好是定点 $F$ 到直线 $l$ 所作垂线段的中点。将式 2 改写为 $y$ 关于 $x$ 的函数形式，可得：

\begin{equation} y = \frac{1}{2p}x^2~. \end{equation}

　　 这个式子正是一个开口向上的二次函数，其图像是顶点在原点、对称轴为 $y$ 轴的曲线。换句话说，从 “点到定点的距离等于它到定直线的距离” 这一条件出发，所得到的轨迹，恰好就是一条抛物线。事实上，这个条件本身也就是抛物线的定义。

定义 1　抛物线

　　 在平面上，所有满足到一条直线 $l$ 与该直线外一固定点 $F$ 的距离相等的点 $P$ 的轨迹，构成一个几何图形，称为抛物线（parabola）。即，对于抛物线上的任意一点 $P$，都有：

\begin{equation} |PF| = d(P, l)~. \end{equation}
其中，$F$ 被称为抛物线的焦点（focus），$l$ 被称为抛物线的准线（directrix），而焦点与准线之间的距离 $d(F, l)$ 被称为抛物线的焦准距（focal parameter），记作 $p$。

　　 根据初中所学，抛物线具有一条对称轴和一个顶点。结合几何定义来看，对称轴（axis of symmetry）是指过焦点并垂直于准线的直线，而顶点（vertex）则是焦点到准线所作垂线段的中点。在抛物线所分割的平面中，约定包含焦点的一侧为抛物线的内部，而包含准线的一侧为其外部。

　　 虽然所有的二次函数图像都是抛物线，但从几何角度来看，抛物线的形状并不取决于它在坐标系中的具体位置。图像放在哪里只会影响它的代数表达式，而不会改变它的几何特征。事实上，任何抛物线都可以通过平移或旋转，化为顶点在原点、对称轴与 $x$ 轴或 $y$ 轴重合的标准形式。因此，在高中阶段的学习中，通常只研究这种标准位置下的抛物线，以便更方便地进行分析和计算。

　　 根据抛物线的定义，可以推导出一个简单但直观的几何性质：作一条与准线平行的直线 $L$，若 $L$ 与准线位于焦点的两侧，那么对于抛物线上的任意一点 $P$，其到焦点的距离 $r$ 与到直线 $L$ 的距离之和是一个定值；反之，若 $L$ 与准线在焦点同侧，则对于任意一点 $P$，其到焦点的距离 $r$ 与到直线 $L$ 的距离之差的绝对值是一个定值。

图
图 2：抛物线的几何性质

　　 以 $L$ 与准线位于焦点两侧的情形为例，如 图 2 所示，记 $O$ 为抛物线焦点，过点 $P$ 作一条垂直于准线的直线，与准线交于点 $A$，与 $L$ 交于点 $B$。根据抛物线的定义有 $|PA| = |OP|$，因此有：

\begin{equation} |AB|=|PA| +|PB| =|OP| +|PB|~. \end{equation}
线段 $AB$ 的长度是固定的，因此 $|OP| +|PB|$ 的值在点 $P$ 变化时保持不变，恒为常数。同侧证明方法也类似，读者可尝试证明。

2. 抛物线的方程

　　 接下来将以 式 2 为基础，考察处于其他 “标准位置” 的抛物线的方程。首先，若将 例 1 中的定点改设为 $F_1(p,0)$，准线改为 $x = -p$，这相当于将原先的 $x$ 轴与 $y$ 轴互换，得到的表达式为：

\begin{equation} y^2 = 2px~. \end{equation}
其次，依据二次函数的知识，若想改变 式 3 中抛物线的开口方向，只需在二次项前添加负号，即可得到：
\begin{equation} y = -\frac{1}{2p}x^2 \quad \Longrightarrow \quad x^2 = -2py~. \end{equation}
综上，可以归纳出抛物线标准方程。

定理 1　抛物线的标准方程

　　

  • 焦点在 $y$ 轴正半轴上的抛物线标准方程：
    \begin{equation} x^2=2py,\qquad(p>0)~. \end{equation}
  • 焦点在 $y$ 轴负半轴上的抛物线标准方程：
    \begin{equation} x^2=-2py,\qquad(p>0)~. \end{equation}
  • 焦点在 $x$ 轴正半轴上的抛物线标准方程：
    \begin{equation} y^2=2px,\qquad(p>0)~. \end{equation}
  • 焦点在 $x$ 轴负半轴上的抛物线标准方程：
    \begin{equation} y^2=-2px,\qquad(p>0)~. \end{equation}

　　 有些读者可能认为无需区分这四种标准方程，只需记住两种基本形式，再根据 $p$ 的正负来判断开口方向，同时将 $|p|$ 理解为抛物线的焦准距。这种记忆方式是可以接受的。不过，在教材中通常采用如上所示的四种形式，是因为参数 $p$ 并不仅出现在此处。为保持定义和表达的一致性，避免在后续内容中引起混淆，故约定 $p$ 为正，通过符号体现抛物线的开口方向。

　　 定理 1 中的四个标准方程，分别对应图 图 3 中开口向上、向下、向右、向左的四种抛物线情形。

图
图 3：标准抛物线

　　 此外，抛物线当然还可以使用参数方程来描述，它本身的关系比较简单，形式上也容易理解。

定理 2　抛物线的参数方程

  • 焦点在 $y$ 轴正半轴上的抛物线参数方程：
    \begin{equation} \begin{cases} x = 2pt \\ y = 2pt^2 \end{cases},\qquad t \in \mathbb{R}~. \end{equation}
  • 焦点在 $y$ 轴负半轴上的抛物线参数方程：
    \begin{equation} \begin{cases} x = -2pt \\ y = -2pt^2 \end{cases},\qquad t \in \mathbb{R}~. \end{equation}
  • 焦点在 $x$ 轴正半轴上的抛物线参数方程：
    \begin{equation} \begin{cases} x = 2pt^2 \\ y = 2pt \end{cases},\qquad t \in \mathbb{R}~. \end{equation}
  • 焦点在 $x$ 轴负半轴上的抛物线参数方程：
    \begin{equation} \begin{cases} x = -2pt^2 \\ y = -2pt \end{cases},\qquad t \in \mathbb{R}~. \end{equation}

　　 以 式 12 为例，当参数 $t$ 从负变为正时，对应的点沿着抛物线从左侧向右侧移动。这种形式能更方便地反映点在轨迹上的运动过程。在具体问题中，还可以根据需要对参数方程进行适当调整，以适配不同方向或位置的抛物线。

抛物线族

　　 与椭圆或双曲线可以通过两个独立的参数分别控制 $x$、$y$ 方向的变化不同，标准形式的抛物线只由一个参数 $p$ 控制其开口程度。如果希望改变抛物线对称轴的方向，不能通过调整参数值实现，而需要通过改变二次项所对应的变量，也就是修改变量的名称来完成。从 “族” 的角度看，所有对称轴相同，仅参数 $p$ 不同的抛物线可以看作是一个抛物线族。

　　 比较特别的是，所有抛物线在几何上彼此都是相似图形。这一点与椭圆和双曲线有本质区别。对于椭圆和双曲线，只有当参数满足一定比例关系时，图形之间才可能相似3。

　　 这一特性也容易证明。设有两个开口方向一致、对称轴为 $x$ 轴的抛物线，其对应参数为 $p_1$ 与 $p_2$，记 $\displaystyle k = \frac{p_1}{p_2}$，则只需在 $x$ 方向保持不变、在 $y$ 方向作 $k$ 倍伸缩，就可将一个抛物线变换为另一个。而若两个抛物线的对称轴不重合，只需先将其通过旋转调整至相同方向，再作适当的缩放，即可实现重合。

　　 这说明，任意两个抛物线都可以通过相似变换（包括旋转与缩放）相互转化，因此在几何意义上，所有抛物线都是相似的图形。

3. 抛物线的几何性质

　　 首先来回答最开始提到的问题，抛物线与双曲线最大的区别是，抛物线没有渐近线。以 式 10 为例，设抛物线上的点为 $P(x, \sqrt{2px})$，考虑任意一条直线 $L: y = ax + b$，分析当 $x \to +\infty$ 时，点 $P$ 到直线 $L$ 的距离变化情况：

\begin{equation} \begin{split} \lim_{x \to +\infty} d(P, L) &= \lim_{x \to +\infty} \frac{|ax - \sqrt{2px} + b|}{\sqrt{a^2 + 1}}\ &= \frac{1}{\sqrt{a^2 + 1}} \lim_{x \to +\infty} | \sqrt{x} \left( a\sqrt{x} - \sqrt{2p} \right) + b |~. \end{split} \end{equation}

　　 从结果可以看出，随着 $x$ 的增大，分子部分 $|ax - \sqrt{2px} + b|$ 也趋于无穷，因此距离不收敛于 $0$。这说明任意一条直线都无法与抛物线无限接近，也就意味着抛物线没有渐近线。这是抛物线与双曲线在图像性质上的一个最显著区别。

切线

　　 先看切线的斜率，一方面对式 3 求导可知：

\begin{equation} y'={p\over x}~. \end{equation}
另一方面，对式 6 ，由隐函数求导可知：
\begin{equation} 2y'y=2p\implies y'={p\over y}~. \end{equation}
参数为负时同样处理即可。这里务必注意 $p$ 在分子上。

　　 根据式 17 和式 18 分别代入式 3 和式 6 得到切线方程：

\begin{equation} y-y_0={x_0\over p}(x-x_0)\quad\implies\quad x_0x=2p\left(\frac{y+y_0}{2}\right)~. \end{equation}
\begin{equation} y-y_0={p\over y_0}(x-x_0)\quad\implies\quad y_0y=2p\left(\frac{x+x_0}{2}\right)~. \end{equation}
这个结果很有趣，与之前椭圆、双曲线的切线形式类似，二次项需要将其中一个变量替换为点的坐标。而特别的是，一次项部分则需要替换成 “点与变量的均值”4。

抛物线的反射性质

定理 3　抛物线反射性质

　　 设抛物线的焦点为 $F$，准线为 $l$，点 $P$ 是抛物线上的任意一点。过点 $P$ 作直线 $l$ 的垂线 $m$，则线段 $FP$ 所在直线与 $m$ 关于点 $P$ 处的切线 $n$ 对称。即：

\begin{equation} \angle(FP, n) = \angle(m, n)~. \end{equation}

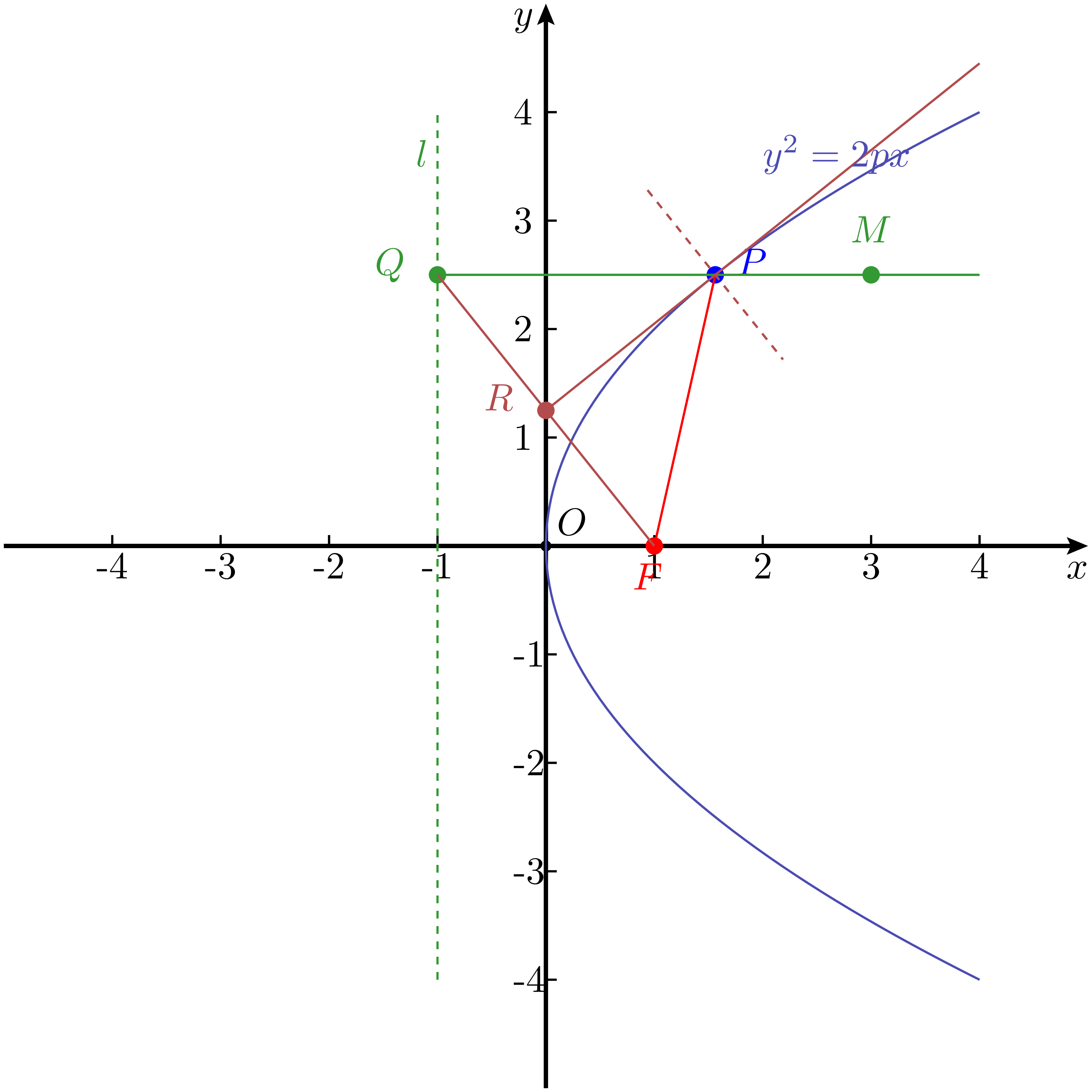
　　 这一性质说明：若从焦点 $F$ 发出一条光线射向抛物线上任意一点 $P$，该光线在 $P$ 处发生镜面反射后，将沿与准线垂直的方向传播（即平行于对称轴）。反之，若一束与对称轴平行的光线射向抛物线并在点 $P$ 处反射，则反射光线将通过焦点 $F$。也就是说，抛物线能够将来自焦点的光线反射为平行光线，或者将平行光线汇聚到焦点。这正是抛物线在探照灯、雷达天线、太阳能集热器等装置中广泛应用的理论基础。

　　 这个结论其实并不难证明。设抛物线的方程为 $y^2 = 2px$，则其焦点为 $\displaystyle F\left(\frac{p}{2}, 0\right)$，准线为 $\displaystyle l: x = -\frac{p}{2}$。在抛物线上取一点 $P(x_0, y_0)$，连接 $PF$，并作 $P$ 到准线 $l$ 的垂线，垂足记作 $Q\left( \displaystyle -\frac{p}{2}, y_0 \right)$。

图
图 4：抛物线的反射性质示意图

　　 根据抛物线的定义，有：

\begin{equation} |FP| = |PQ|~. \end{equation}
也就是说，$\triangle PQF$ 是一个等腰三角形。设 $R$ 为底边 $FQ$ 的中点，根据中点公式，$R$ 的坐标为 $\displaystyle \left( 0, \frac{y_0}{2} \right)$。由等腰三角形的性质可知，$PR$ 是 $\angle FPQ$ 的角平分线，换句话说，$PF$ 和 $PQ$ 关于 $PR$ 对称。

　　 根据式 18 ，点 $P$ 处抛物线的切线为：

\begin{equation} y-y_0={p\over y_0}(x-x_0)~. \end{equation}
将 $x = 0$ 代入切线方程，并结合抛物线方程 $y_0^2 = 2px_0$ 进行化简，得到 $y$ 轴截距：
\begin{equation} \begin{split} y&=y_0-{px_0\over y_0}\\ &=y_0-{y_0^2\over 2}\cdot{1\over y_0}\\ &={y_0\over 2}~. \end{split} \end{equation}
因此，这条切线恰好通过点 $R$，即 $PR$ 是点 $P$ 处的切线。而前面已经知道 $PF$ 和 $PQ$ 关于 $PR$ 对称，于是可以得出结论——抛物线上的任意一点，其到焦点的连线与到准线的垂线，关于该点的切线对称。

1. ^ 其实还可以换一种方式来看：此时也可以理解为 $\displaystyle \frac{|O_1P|}{|O_2P|} = 1$，然后将定义推广为这个比值为任意常数 $k$，就会得到一种新的轨迹，这类图形被称为阿波罗尼斯圆（Apollonius circle）。
2. ^ 之所以可以进行这样的替换，其实是因为在射影几何的视角下，点和线之间是可以互相转换的。具体内容可参见 圆锥曲线的统一定义。
3. ^ 对于椭圆，是长轴与短轴的比例相同；对于双曲线，是渐近线的夹角相同。这个比例对应着一个非常重要的参数：离心率，参见圆锥曲线的统一定义
4. ^ 这个规律是标准形式下的一个特例，在一些非标准形式或更高次幂的情况下，不能直接套用。感兴趣的读者可以尝试自行推导。

                     

© 保留一切权利