贡献者: addis
本文使用原子单位制。类氢原子(hydrogen-like atom)被定义为原子核有 $Z$ 个质子(核电荷为 $+Ze$)但只有一个核外电子的原子或离子,例如氢原子($Z=1$)、失去一个电子的氦原子 $\mathrm{He}^+$($Z=2$)和失去两个电子的锂离子 $\mathrm{Li}^{++}$($Z=3$)。
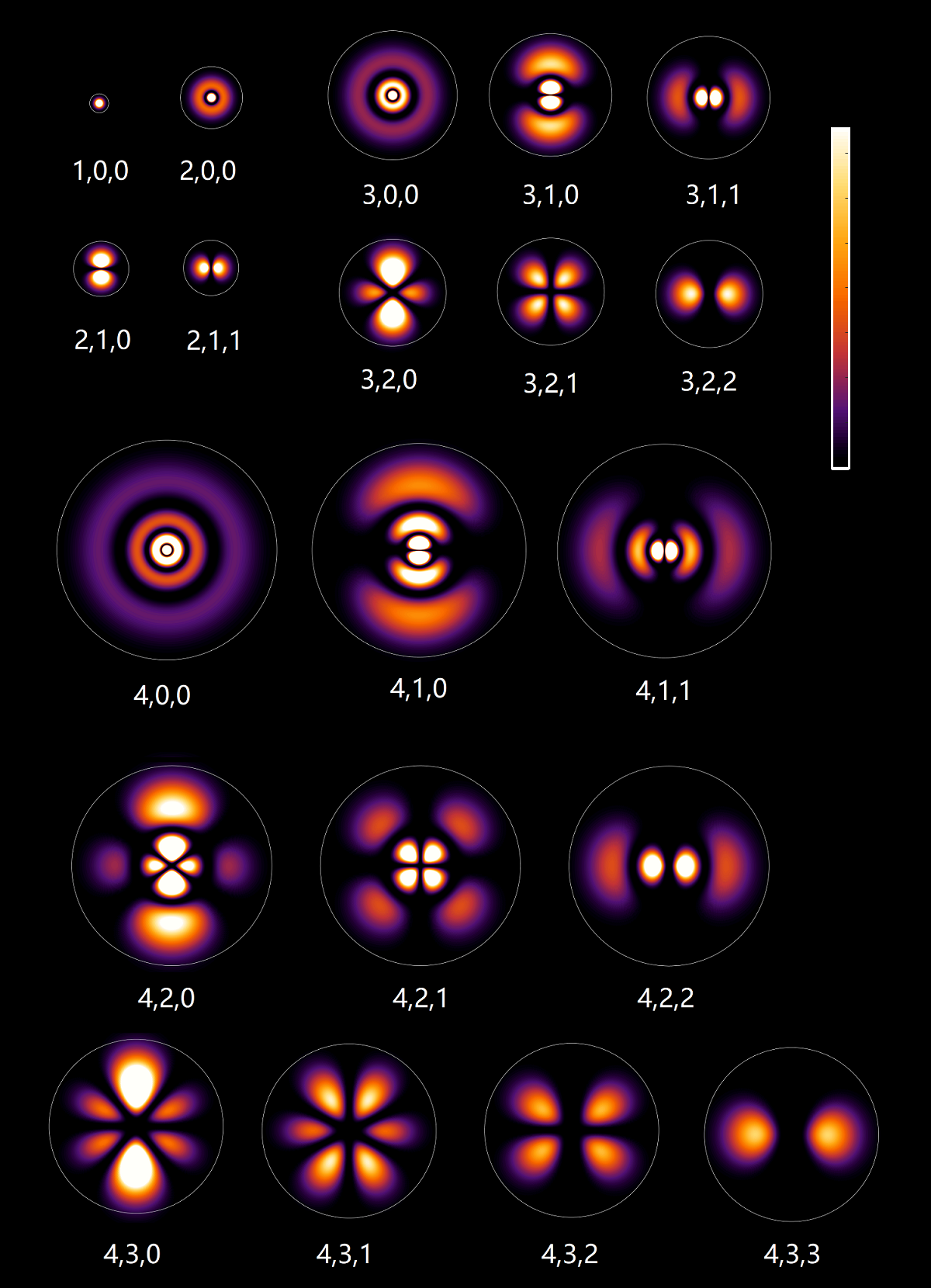
图 1:氢原子波函数的概率密度 $ \left\lvert \psi_{n,l,m}( \boldsymbol{\mathbf{r}} ) \right\rvert ^2$ 的 $x$-$z$ 截面,相对大小成比例。每个图中的三个数字分别是量子数 $n, l, m$,电子出现在白色圆圈内部的概率为 0.95。色条对应的数值是线性的,每个子图中的色条取值范围不相同。源码见 “
氢原子波函数画图程序(Matlab)”。
类氢原子的定态薛定谔方程为(式 1 ,原子单位制库仑势能 $V(r)=-Z/r$,电子质量 $m=1$)
\begin{equation}
-\frac{1}{2m} \boldsymbol{\nabla}^2 \psi( \boldsymbol{\mathbf{r}} ) - \frac{Z}{r} \psi( \boldsymbol{\mathbf{r}} ) = E \psi( \boldsymbol{\mathbf{r}} )~,
\end{equation}
类氢原子是唯一存在解析解的原子(离子)。该方程假设原子核不动,若要考虑原子核的运动,应该类似 “
玻尔原子模型(约化质量)” 在
式 1 使用约化质量 $\mu$ 代替电子质量 $m$。
我们这里只讨论束缚态,即 $E < 0$ 的可归一化的解。1由于原子核的库仑势能具有球对称性,球坐标下的波函数具有最简单的形式。用分离变量法解式 1 ,得波函数的表达式为
\begin{equation}
\psi_{n,l,m}( \boldsymbol{\mathbf{r}} ) = \psi_{n,l,m}(r,\theta ,\phi) = R_{n,l}(r) Y_{l,m}(\theta, \phi)~.
\end{equation}
其中 $n$ 是
主量子数($n = 1, 2, \dots$),$l$ 是
角量子数($l = 0, 1, \dots, n - 1$),$m$ 是
磁量子数($m = -l, -l+1, \dots, l$)。$R_{n,l}(r)$ 是归一化的
径向波函数(见下文),$Y_{l,m}(\theta, \phi)$ 是归一化的
球谐函数(另见
球谐函数表)。波函数概率密度的截面图如
图 1 。
2
波函数 $\psi_{n,l,m}$ 是能量本征态,对应的能级(本征值)为
\begin{equation}
E_n = - \frac{m e^4}{32 \pi^2 \epsilon_0^2 \hbar ^2} \frac{Z^2}{n^2} \approx - 13.6 \,\mathrm{eV} \frac{Z^2}{n^2}
\qquad (n = 1, 2, \dots)~,
\end{equation}
考虑原子核运动时同样要把 $m$ 替换成 $\mu$。注意能级之和主量子数 $n$ 有关,多个不同的波函数具有相同能级的情况叫做
简并,所以易得第 $n$ 能级有 $n^2$ 重简并。
容易发现玻尔原子模型的能级和该式恰好相同,且都与氢原子光谱吻合,这也是当初人们接受玻尔模型的重要原因。但使用薛定谔方程才是真正符合量子力学的方法,因为波尔模型无法解释许多其他问题如多电子原子的能级。
1. 氢原子的径向波函数
现在来解式 2 中的径向波函数 $R_{n,l}(r)$。球坐标系的薛定谔方程在分离变量后,可得(约化)径向方程式 3 ,其中 $V(r) = -Z/r$。对任意给定的 $E < 0$ 和 $l = 0,1,2,\dots$,令 $\rho = \kappa r$,$\eta = -Z/\kappa$,$\kappa = \sqrt{-2mE}$,径向方程化简为
\begin{equation}
\frac{\mathrm{d}^{2}{u}}{\mathrm{d}{\rho}^{2}} + \left[-1 - \frac{2\eta}{\rho} - \frac{l(l+1)}{\rho^2} \right] u = 0~.
\end{equation}
它的通解
3为
\begin{equation}
\psi_{E,l}(x) = C_1 M_{-\eta, l+1/2}(2 \rho) + C_2 W_{-\eta, l+1/2}(2 \rho)~.
\end{equation}
$M, W$ 分别是 Whittacker M 和 W 函数,$x = 0$ 时,$M$ 函数总是为零,而 $W$ 可能不为零,所以符合物理的解必须 $C_2 = 0$。另外可以证明只有对
式 3 中离散的 $E_n$,波函数才能归一化得到束缚态。束缚态的径向波函数可以化简为(
式 5 乘以 $1/r$)
\begin{equation}
R_{n,l}(r) = \sqrt{ \left(\frac{2 Z}{n} \right) ^3 \frac{(n - l - 1)!}{2n (n + l)!}} \left(\frac{2Zr}{n} \right) ^l L_{n-l-1}^{2l+1} \left(\frac{2Zr}{n} \right) \mathrm{e} ^{-Zr/n}~,
\end{equation}
其中 $L_n^l(x)$ 是
连带拉盖尔多项式(associated Laguerre polynomial)。注意 $Z$ 的作用是把径向波函数关于原点缩小 $Z$ 倍,并保持波函数归一化。
$Z = 1$ 时 $r R_{n,l}(r)$ 的函数图4如图 2
图 2:径向波函数函数图(使用原子单位)
以下给出前几个径向波函数,注意所有径向波函数的值都是实数。
\begin{equation} n = 1 \qquad
R_{10}(r) = 2 Z^{3/2} \mathrm{e} ^{-Zr}~,
\end{equation}
\begin{equation}
n = 2 \qquad
\left\{\begin{aligned}
R_{20}(r) &= \frac{1}{\sqrt 2} Z^{3/2} \left(1 - \frac12 Zr \right) \mathrm{e} ^{-Zr/2}\\
R_{21}(r) &= \frac{1}{2\sqrt{6}} Z^{3/2} Zr \mathrm{e} ^{-Zr/2}
\end{aligned}\right. ~,\end{equation}
\begin{equation}
n = 3 \qquad
\left\{\begin{aligned}
R_{30}(r) &= \frac{2}{3\sqrt {3}} Z^{3/2} \left(1 - \frac23 Zr + \frac{2}{27} Z^2r^2 \right) \mathrm{e} ^{-Zr/3}\\
R_{31}(r) &= \frac{8}{27\sqrt 6} Z^{3/2} \left(1 - \frac16 Zr \right) Zr \mathrm{e} ^{-Zr/3}\\
R_{32}(r) &= \frac{4}{81\sqrt {30}} Z^{3/2} Z^2r^2 \mathrm{e} ^{-Zr/3} \end{aligned}\right. ~.
\end{equation}
更多 $R_{n,l}$ 和 $\psi_{n,l,m}$ 表达式可以用
Mathematica 或者
Wolfram Alpha 生成,函数定义如
HydrogenR[Z_, n_, l_, r_] := Sqrt[(2Z/n)^3\
Factorial[n-l-1]/(2n Factorial[n+l])] (2Z r/n)^l\
LaguerreL[n-l-1, 2l+1, 2Z r/n] Exp[-Z r/n];
HydrogenPsi[Z_, n_, l_, m_, r_, θ_, ϕ_] :=
HydrogenR[Z, n, l, r] SphericalHarmonicY[l, m, θ, ϕ];
或者用 Matlab 进行数值计算
代码 1:hydrogen_Rnl.m
function ret = hydrogen_Rnl(Z,n,l,r)
ret = sqrt((2*Z/n)^3*factorial(n-l-1)/(2*n*factorial(n+l))) *...
(2*Z*r/n).^l .* laguerreL(n-l-1, 2*l+1, 2*Z*r/n) .* exp(-Z*r/n);
end
代码 2:hydrogen_Psi.m
function ret = hydrogen_Psi(Z,n,l,m,r,th,ph)
ret = hydrogen_Rnl(Z,n,l,r) .* SphHarm(l,m,th,ph);
end
2. 性质
我们要求氢原子每个束缚态满足正交归一化条件
\begin{equation} \begin{aligned}
&\int \Psi_{n',l',m'} ^* ( \boldsymbol{\mathbf{r}} )\Psi_{n,l,m}( \boldsymbol{\mathbf{r}} ) \,\mathrm{d}^{3}{r} \\
= &\int \int_0^\infty R_{n',l'} ^* (r) Y_{l',m'}( \hat{\boldsymbol{\mathbf{r}}} )R_{n,l}(r) Y_{l,m}( \hat{\boldsymbol{\mathbf{r}}} ) r^2 \,\mathrm{d}{r} \,\mathrm{d}{\Omega} = \delta_{n,n'}\delta_{l,l'}\delta_{m,m'}~.
\end{aligned} \end{equation}
根据
式 5 和
式 8 可得径向波函数的归一化条件
\begin{equation}
\int_0^\infty R_{n', l}(r) R_{n,l}(r) r^2 \,\mathrm{d}{r} = \delta_{n,n'}~.
\end{equation}
注意对不同的 $l$,无论 $n,n'$ 相同或不同,径向波函数都未必正交。
Mathematica 代码如(式 10 中 $\Psi_{2,1,0}$ 和 $\Psi_{3,1,0}$ 的积分)
Z = 1; Integrate[
Conjugate[HydrogenPsi[Z, 2, 1, 0, r, th, phi]] HydrogenPsi[
Z, 3, 1, 0, r, th, phi] r^2 Sin[th], {r,
0, Infinity}, {th, 0, Pi}, {phi, 0, 2 Pi}]
3. 径向概率分布
我们来求径向概率分布 $P(r)$。$P(r)$ 的定义为:发现粒子在 $r \in [a, b]$(厚球壳)内的概率为 $\int_a^b P(r) \,\mathrm{d}{r} $。由于波函数的模长平方就是三维的概率密度,有
\begin{equation}
\int_a^b P(r) \,\mathrm{d}{r} = \int_a^b \int \left\lvert \frac1r \psi_{l,m}(r) Y_{l,m}( \hat{\boldsymbol{\mathbf{r}}} ) \right\rvert ^2 \,\mathrm{d}{\Omega} r^2 \,\mathrm{d}{r}
= \int_a^b \left\lvert \psi_{l,m}(r) \right\rvert ^2 \,\mathrm{d}{r} ~.
\end{equation}
对任意 $a, b > 0$ 都成立,所以有
\begin{equation}
P(r) = \left\lvert \psi_{l,m}(r) \right\rvert ^2~.
\end{equation}
任意波函数可以表示为所有本征波函数的叠加
\begin{equation}
\Psi( \boldsymbol{\mathbf{r}} ) = \frac1r \sum_{l,m} \psi_{l,m}(r) Y_{l,m}( \hat{\boldsymbol{\mathbf{r}}} )~.
\end{equation}
其径向概率分布为
\begin{equation}
\int_a^b P(r) \,\mathrm{d}{r} = \int_a^b \int \left\lvert \frac1r \sum_{l,m}\psi_{l,m}(r) Y_{l,m}( \hat{\boldsymbol{\mathbf{r}}} ) \right\rvert ^2 \,\mathrm{d}{\Omega} r^2 \,\mathrm{d}{r}
= \sum_{l,m} \int_a^b \left\lvert \psi_{l,m}(r) \right\rvert ^2 \,\mathrm{d}{r} ~.
\end{equation}
对任意 $a, b > 0$ 都成立,所以有
\begin{equation}
P(r) = \sum_{l,m} \left\lvert \psi_{l,m}(r) \right\rvert ^2~.
\end{equation}
4. 动量表象、动量分布
要求动量表象下的波函数,我们需要将位置表象的波函数投影到归一化的动量的本征矢上,即三维傅里叶变换
\begin{equation}
\psi_{n,l,m}( \boldsymbol{\mathbf{p}} ) = \left\langle \boldsymbol{\mathbf{p}} \middle| \psi \right\rangle = \frac{1}{\sqrt{2\pi}} \int \exp\left(- \mathrm{i} \boldsymbol{\mathbf{p}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} \right) \psi( \boldsymbol{\mathbf{r}} ) \,\mathrm{d}^{3}{r} ~.
\end{equation}
这个积分在球坐标中完成才是最方便的,具体方法我们将举例子说明(见
例 1 )。
正如位置表象下位置的分布函数是 $ \left\lvert \psi( \boldsymbol{\mathbf{r}} ) \right\rvert ^2$,动量表象下动量的分布函数是 $ \left\lvert \psi( \boldsymbol{\mathbf{p}} ) \right\rvert ^2$(也符合测量理论)。
1. ^ 如果不要求波函数可归一化,$E$ 取任意实数我们都能找到解。但只有当 $E$ 取特定离散值的时候这些波函数才能归一化,不能归一化的波函数没有物理意义。
2. ^ 为什么图中用 95% 而不是 100%?因为无论离原子核多远电子出现的概率都不会完全等于零,而是一个指数下降的尾巴(exponential tail)。
3. ^ 可以使用 Mathematica 求解
4. ^ 我们以后会看到 $r R_{l,m}(r)$ 比 $R_{l,m}(r)$ 更常用