Mathematica 笔记

                     

贡献者： addis; int256

　　 Mathematica 相对于 Matlab，Python 等偏数值计算的语言最大的特点就是专注于符号计算以及变精度计算（也叫任意精度计算）。其中变精度计算能追踪误差，保证输出结果的最后一位小数正确。

　　 以下笔记详情参考 Mathematica 的官方文档。

待整理

• 官方教程
• Mathematica 的根基是 Expression, 用 FullForm 函数可以查看 Expression 的全称.
• 如果 expression 和 literal constant 运算, 是非常精确的.
• 如果函数不支持 List 输入, Map[Function, {arg1,arg2...}] 可以把一个函数依次作用在一个 List 上面.
• var1=var2=var3=val 可以给 var1,var2,var3 同时赋值, 用 . 给变量赋值可以清除变量的值, 相当于 Clear[var1,var2,var3]
• 如果 x2 = [x1 的表达式], x3=[x2 的表达式], 那么如果输入 x3 会返回 x1 的表达式. 但是 [x2 的表达式] 的信息还在, 因为如果这是把 x2 清空, 输入 x3 又会出现 x2 的表达式.
• 变量名建议用小写开头
• 两个变量用空格隔开代表相乘
• expr_of_x/.x->3 可用于临时赋值表达式中的变量

1. 常识

• Mathematica 最常用的文件格式是 .nb（notebook），里面有各种互动内容如输入，输出，图片，互动演示等，虽然这是个文本文件，但是非常难读，即使是输入的公式，也会保留很多显示格式信息（例如分数，根号是否要立体显示）
• 另一种格式 .m 是纯文本脚本，类似于常规编程语言的手写代码。该文件可以直接用文本编辑器手写，不支持互动和任何多媒体，常用于写软件包（见下文）。.nb 的立体表达式等，都需要转换成具体的命令才可以在 .m 中表示。Mathematica 的编程语言叫做 Wolfram Language。
• 要像 Matlab 一样给代码设置断点逐行调试，可以另外下载官方的 eclipse 插件：Wolfram Workbench。
• 调整字体大小 Ctrl + 鼠标滚轮。
• 快捷键 Shift + Enter 执行选中的行。
• 一行输入多个表达式用分号 “;”，分号也可以用于抑制输出。a = 3; b = 5; a b
• 用 (*注释*) 写注释。注释不会被执行。也可以选中后按 Alt + /。
• 可以用 \ 把较长的文本表达断成几行，每次换行前插入。粘贴到 notebook 以后会变成一行。在 notebook 中直接插入会出错。
• 可以用小数点产生数值解，例如 Sqrt[2.]。
• 空格表示乘号，相当于 *。数字和变量间相乘不需要空格或 *。
• 科学计数法如 2.3*^-70 表示 $2.3 \times 10^{-70} $。
• 变量名不能有下划线！
• 中断执行 Alt + ,（笔记本界面）或者 Ctrl + C（文本界面）。
• 输入 In[8]

符号输入

• 输入符号用 Esc 键搜索，例如搜索 pi 按回车可以插入 π。这相当于输入 Pi 或者 \[Pi]。如果你用过 TeX，也可以按 Esc 键后搜索 tex 命令，例如 \pi。
• 可以在命令行直接粘贴 UTF-8 字符如 θ，注意 φ 和 ϕ 在一些字体中的形状会调换。
• 复制一个符号然后粘贴到一个 txt 文档中，就会得到 \[...] 形式的代码。
• 复制一个表达式然后粘贴到 txt 文档中，默认会得到含有空格和换行符的 plain text 命令，相当于选中后右键 copy as -> input text。如果 copy as -> plain text，一些空格和换行符将不会插入。

常数

• 圆周率：Pi 或 \[Pi] 或搜索 pi。
• 自然对数底：E 或 \[ExponentialE] 或搜索 ee。
• 虚数单位：I 或 \[ImaginaryI] 或搜索 ii。a + I b 表示复数，I 不能用作其他变量名。
• 虚数单位：\[ImaginaryJ] 或搜索 jj。
• 1° 角的弧度：Degree 或 \[Degree] 或搜索 deg。
• 无穷：Infinity 或 \[Infinity] 或搜索 inf。

2. 快捷键

• Ctrl + 鼠标滚轮 调整字体大小。
• Shift + Enter 执行选中的行。
• Ctrl + L 调用最近的输入。
• Ctrl + Shift + L 调用最近的输出。
• Ctrl + - 输入下标。相当于 Subscript[x, y]。注意这不完全是符号，有运算意义。
• Ctrl + 6 输入上标。相当于 x^y
• Ctrl + / 输入分式，相当于 x/y。
• Ctrl + 2 输入根式，相当于 Sqrt[]。
• Alt + ) 或 Alt + ] 或 Alt + } 插入一对括号，光标移动到中间。
• Alt + 1 到 Alt + 6 不同级别的标题
• Alt + 7 正文
• Alt + + 和 Alt + - 用于选中一段文字后改变大小。
• Ctrl+_ 下标（注意下标是有语法含义的，数组等，具体待查）

3. 变量

• Head[...] 可用于判断一个对象的类型，如 Head[1] 是 Integer，Head[Pi] 是 Symbol，Head[1/5] 是 Rational，Head[0.2] 是 Real，Head[I] 是 Complex，Head[Sin[1]] 是 Sin，Head[2 Pi/3] 是 Times。
• Precision[数值] 用于查看某变精度数值的有效位数。小数默认是双精度，也叫 MachinePrecision，例如 Precision[1.] 得 MachinePrecision。
• SetPrecision[表达式， N] 会把表达式中可以求出数值的部分都变为 N 位有效数字，例如常数 Pi，E，又如 Sin[1]。又如 SetPrecision[2/3 x + 2 y, 20]。
• Real 和 Complex 用于浮点运算，有误差。例如计算 SetPrecision[1.3, 30] 最后几位不为零。如果要精确表示 1.23456789，就用 123456789*^-8。
• 所有的变精度计算会追踪误差，运算结果的有效数字一般比输入的有效数字要少，但一定会精确到最后一位。这估计和 Arb 的算法一样。
• 在开始用 WorkingPrecision -> MachinePrecision; 可以把以后的浮点计算都变为双精度而不是变精度的。这会导致计算结果的小数位都是 16 左右，但并不都是对的。这么做的好处是计算速度快。
• 把浮点数变为分数如 Rationalize[3.14159265358, 0]，但最后一位后面可能不为零。但至少之后的计算中就没有误差了。
• 1.2345`10 声明精确到 10 位有效数字，0.012345``10 声明精确到 $1 \times 10^{-10} $。
• 更多精度控制的说明见这个文档。
• ?变量 显示某个变量的定义
• Clear[变量名] 清除某个变量的定义。
• 数组在 Mathematica 中叫做 List（列表），如 data = {a, 2, c, d}，每个元素可以是任意类型的对象。
• T = {{1, 2}, {3, 4, 5}}，是列表的列表。

4. 矩阵与线性代数

• {1,2,3,4} 叫做 List（列表），Mathematica 的矩阵就是列表的列表。
• list 的指标从 1 开始。
• 高维列表就是列表的列表的……每个维度的长度未必需要相等，例如 T = {{1,2}, {3,4,5}}。但如果是矩阵或者高维矩阵（张量）就必须相等。
• TableForm[T] 用于显示矩阵（没有括号）。这是一个单变量函数也可以写成 T // TableForm。
• MatrixForm[T] 用于显示矩阵（有圆括号）。
• TableForm[T] 和 MatrixForm[T] 不再是列表，所以只用它们来显示而不要用来赋值。例如矩阵乘法 MatrixForm[A] . MatrixForm[B] 不会返回最后结果。
• Mathematica 的矩阵是行主序的，可以把三维矩阵/数组第一个指标看作列，第二个看作行，第三个看作指向屏幕内的方向。元素写成一行的顺序是先增加最右边（最内层）的指标，再增加右边第二个……越左边的指标是最外层的 list。
• MatrixForm 显示高维数组的时候仍然把 1,2 个指标显示为矩阵，每个元素是一个矩阵，指标是 3,4，以此类推。
• ConstantArray[c, {n1,n2,...}] 可以生成常数元素的高维矩阵。
• Dimensions[a] 可以获得矩阵各个维度的尺寸。如果 list 的每个元素长度或类型不同，那么 Dimension[list] 只返回第一个维度的尺寸。
• a[[i]] 获取一维列表元素，或者二维列表的第 $i$ 行。
• a[[-1]] 表示最后一个元素，a[[-2]] 倒数第二个元素。
• a[[0]] 输出 Head[a]，无论 a 是不是列表。
• a[[i, j]] 获取二维列表元素的元素，或者三维列表的一个最内层花括号。
• a[[All, j]] 获取一列，a[[i, All]] 获取一行。
• a[[2;;4]] 获取第 2,3,4 个元素。
• a[[2;;]] 获取第 2 个到最后一个元素，a[[;;4]] 获取第一个到第 4 个元素
• a[[2;;9;;3]] 获取元素 2, 5, 8。a[[2;; ;;3]] 获取元素 $2, 5, 8, \dots$ 直到最后。
• 合并矩阵/矢量 Join[{{1,2},{3,4}},{{5,6},{7,8}}] 得 {{1,2},{3,4},{5,6},{7,8}}，在第 1 个维度上合并。等效于 Join[{{1,2},{3,4}},{{5,6},{7,8}},1]
• Join[{{1,2},{3,4}},{{5,6},{7,8}},2] 得 {{1,2,5,6},{3,4,7,8}}，在在第 2 个维度上合并。
• Mathematica 中把若干矢量排列成矩阵都是按行排列。例如 Eigenvector 返回的本征矢。
• Dot 点乘，也可以用 .。例如 {1, 1+I}.{3, 4}。注意第一个向量不会进行共轭。
• Norm 计算矢量的模长，Norm[{3,4}] 结果是 5。
• Transpose[] 可以把矩阵做转置。也可以在矩阵后面用 \[Transpose] 或者 Esc 键搜索 tr。
• ConjugateTranspose[] 可以把矩阵做厄米共轭。也可以在矩阵后面用 \[HermitianConjugate] 或者 Esc 键搜索 hc。
• LinearSolve[{{1, 2}, {3, 4}}, {5, 6}] 解线性方程组。
• Eigenvectors[{{1,2},{3,4}}]，Eigenvalues[{{1,2},{3,4}}] 计算矩阵本征值。或者 EigenSystem[矩阵]，一次返回 {本征值，本征矢}，和分别计算是一样的。注意返回的本征矢矩阵每行是一个本征矢而不是每列。注意符号计算时返回的本征矢未必是归一化也未必是正交的（因为这往往需要很久表达式也很复杂），数值计算时返回的是正交归一本征矢。
• Orthogonalize[] 可以把矢量的 list 正交归一化（如果看成矩阵，则每行是一个矢量）。
• MatrixExp[A] 计算矩阵的指数 $ \mathrm{e} ^{A}$。

5. 算符

• +, -, *, ^ 把两个矩阵进行逐个元素的运算。
• . 矩阵乘法
• = 立即赋值（赋值时立刻计算右边，最终结果赋给左边）
• := 延迟赋值（每次需要左边时都替换为右边）
• != 不等号
• 连接字符串 "abc" <> "defg" <> "hij"。
• 单变量的函数 f[...] 也可以用后缀形式记为 ... // f 或者用前缀形式记为 f @ ...。
• /. 是 ReplaceAll[] 的简写形式，用于替换表达式中的符号。例如 {x, x^2, y, z} /. x -> 1 的结果是 {1,1,y,z}，又例如 {x, x^2, y, z} /. {x -> y, y -> z, z -> x}
• Sin'[x] 相当于 D[Sin[x], x]，Sin''[x] 相当于 D[Sin[x], {x,2}]
• x =. 清除符号 x 的定义。
• Remove[x] 完全清除符号。
• i++ 和 ++i 和 -- 与 C 语言中用法相同。
• x ∈ dom 或 x \[Element] dom 相当于 Element[x, dom]
• 2 > 1 相当于 Greater[2, 1]，返回 True。2 < 1 相当于 Less[2, 1], 返回 False。

6. 判断循环

• 判断如 If[条件, 真执行命令, 假执行命令] 其中 假执行命令 可以省略。
• 循环如 For[i = 1, i <= 10, i++, A[[i]] = i^2]。
• 嵌套循环如 For[i = 1, i <= 10, i++, For[j = 1, j <= 10, j++, A[[i, j]] = i + j]]。
• Break[] 和 Continue[] 和 C 语言用法一样。

7. 函数

• 定义函数 f[x_, y_] := x^2 + y^2。左边的自变量需要用下划线。
• 更复杂的函数也可以用 Module[] 定义如 f[x0_] := Module[{x = x0}, While[x > 0, x = Log[x]]; x]。格式为 Module[{a,b,...}, expr]，或 Module[{a=1,b=2,...}, expr] 其中第一个大括号中声明本地变量以及初始化（大括号中可以为空），expr 可以由许多分号隔开，最后一个是函数的返回值。
• 注意 Module 定义的函数不支持一些符号运算，例如 D[f[x]] 会得到错误的结果。
• 匿名函数 ...#...&[...] 中 & 之前就是函数的定义，可以把方括号中的内容的变量在左边用 # 代替，如 # Sin[#] &[x] 得到函数 x Sin[x]。又例如 #.#\[Transpose] &[RandomInteger[{-5, 5}, {6, 6}]] 可以随机生成对称矩阵。也可以用 @ 代替方括号。
• 如果一个函数返回一个 list，可以用 {a,b,..} = Fun[...] 把每个元素分别赋给不同变量。这是事实上不是函数的功能，{a, b, c} = {{1, 2}, 2, "c"} 也可以对 a,b,c 分别赋值。
• 变量默认值：foo[a_, b_:2, c_:3] := bar[a, b, c] 输入 foo[1] 返回 bar[1,2,3]
• 函数选项：先用 Options[函数名] 定义选项的名字和默认值，再把 OptionsPattern[] 作为函数定义的某个参数。例如 Options[fun] = {"a" -> 1, "b" -> 2}; fun[x_, OptionsPattern[]] := {x, OptionValue[a], OptionValue[b]}; 调用时例如 fun[0, b->3]，返回 {0, 1, 3}

8. 常用函数

• Print["a = ", a, " b = ", b]。
• 函数参数中，下标在上标之前给出，例如勒让德多项式 $P_n^m(x)$ 为 LegendreP[n, m, x]。
• Max[x1, x2, ...] 或 Min[x1, x2, ...] 求最大最小值，参数也可以使用一个 list。
• 函数 N[表达式, 有效位数] 把表达式的结果变为数值，四舍五入到指定的有效数字，第二个参数可省略。例如 N[Pi] 计算圆周率的前 5 位，N[Pi, 1000] 计算 1000 位。
• Re[z]， Im[z] 计算复数的实部和虚部。
• Conjugate[z] 复共轭，也可以用 z\[Conjugate] 显示为星号。
• Abs[z] 复数的绝对值
• Arg[z] 复数的辐角
• Factor[x^25-1] 因式分解
• Expand[(a+b)^3] 多项式展开
• DSolve[{y''[x] + b y'[x] == 0, y[0] == 0, y'[0] == 1}, y[x], x] 解常微分方程。也可以省略初始条件获得通解。也可以在后面加上假设如 Assumptions -> {a \[Element] Reals}。又例如 a > 0 声明非负实数。如果要多个假设，用 Assumptions -> {assumption1 && assumption2 && ...}
• Piecewise[{{x^2, x < 0}, {x, x > 0}}] 分段函数。
• Table[i^2, {i,3}] 输出 {1, 4, 9}。
• FullSimplify[表达式] 简化表达式。
• Clear["Global`*"] 清除当前进程中的所有定义。
• Range[5]，Range[2, 5] 输出 {1,2,3,4,5}，{2,3,4,5}。
• Select[List, 条件函数] 从 List 中选择使得条件函数返回 True 的子 List，保持排序不变。如 Select[{1, 2, 4, 7, 6, 2}, # > 2 &] 输出 {4,7,6}
• Cases[List, 条件] 从 List 中选出符合条件的子 List，如符号，整数，函数参数等
• Sort[{1, 3, 2, 5, 4}] 把列表升序排序，Sort[{1, 3, 2, 5, 4}, Greater] 降序排序。
• 排序时同时排序另一个数组：ordering = Ordering[list1]; sortedList1 = list1[[ordering]]; sortedList2 = list2[[ordering]];
• Map[f, Range[3]] 输出 {f[1], f[2], f[3]}。
• /@ 是 Map 的简写形式 f /@ Range[3]。
• 分段函数 f[x_] := 0 /; x < -1 以及 f[x_] := 1 /; x > -1 && x < 1 等。
• Listable 的函数可以直接 Sin[Range[3]]。Atributes[Sin]
• 求和 Sum[f, {i, imin, imax}]
• 对列表求和用 Total[{1,2,3}]。高维矩阵默认对第一个指标求和，把后面的指标依次向前移。Total[高维矩阵, n] 对前 $n$ 个指标求和，后面指标向前移。Total[高维矩阵, {n}] 对第 $n$ 个指标求和，后面的指标向前移。
• Product[x + i, {i, 2, 4}] 输出 (2 + x)(3 + x)(4 + x)。

微积分

• Solve[左边==右边, x] 求解关于 $x$ 的方程。
• Roots[左边==右边, x] 和 Solve 相同，但结果的格式不同。
• Limit[f, x->x0] 极限 $\lim_{x\to x_0} f$。
• Minimize[f, x]，Maximize[f, x] 求函数 $f(x)$ 的最小值/最大值。
• Series[f, {x, x0, order}] 把函数展开成泰勒级数。
• D[Sin[x]]，D[Sin[x+y],x]，导数和偏导数。
• Integrate[1/(x^3-1),x] 不定积分，Integrate[f,{x, xmin, xmax}] 定积分, Integrate[f, {x, xmin, xmax},{y, ymin, ymax},...] 重积分。
• Integrate[(f[x])\[Conjugate] f[x], {x, -\[Infinity], \[Infinity]}, Assumptions -> {\[Sigma] > 0, Subscript[k, 0] > 0, x0 > 0}] 中使用限制一些常数的范围，这会大大缩短计算时间，如果不规定范围，则默认是任意复数。
• 若要假设一个数为实数，用 Assumptions -> {x \[Element] Reals}
• FourierSeries[函数, 自变量, 项数]。
• FourierTransform[Exp[-x^2], x, k] 傅里叶变换。

数值运算

• NIntegrate[f, {x, xmin, xmax}] 数值积分。
• NSolve[左边==右边, x] 求解关于 $x$ 的方程。
• NSolve[..., WorkingPrecision -> n] 可以规定精度。也可以用于例如 NIntegrate[]。
• 如果 NIntegrate 显示迭代次数超出限制，可以用 MaxRecursion -> 次数 增加迭代次数。
• NMinimize[f, x]，NMaximize[f, x] 求函数 $f(x)$ 的最小值/最大值。
• NDSolve[{y'[x] == y[x] Cos[x + y[x]], y[0] == 1}, y, {x, 0, 30}] 数值解常微分方程。把结果画图：Plot[Evaluate[y[x] /. s], {x, 0, 30}, PlotRange -> All]。

9. 画图

• Plot[y[x], {x, -5, 5}] 简单的画图。Plot[{y1[x],y2[x],...}, {x, -5, 5}] 画多条曲线。
• 通过散点画折线图用 ListLinePlot[{{x1,y1},{x2,y2},...}] 如果省略 x，那么默认 x=1,2,3,...。或者画多条线 ListLinePlot[{{y1,y2,...},{z1,z2...}}]（默认 x=1,2,3,...）。第二个参数用 Mesh -> All 可以除了折线还画出数据点。
• Plot[] 或者 ListPlot[] 添加图例：Plot[{x^2, 3 x}, {x, -5, 5}, PlotLegends -> {"图例1", "图例2"}]。
• Plot 和 ListLinePlot 的更多性质见这里。
• 要在一张图上画多个不同内容用 Show[命令1, 命令2]，例如 Show[Plot[2 x^2, {x, 0, 4}], ListLinePlot[{{1,2,3}, {2,3,4}}, Mesh -> All]]。
• 一次画多个函数 Plot[{Sin[x], Sin[2 x], Sin[3 x]}, {x, 0, 2 Pi}, PlotLegends -> "Expressions"]

3D 画图

• Plot3D[Sin[y+Sin[3x]], {x,-3,3}, {y,-3,3}] 简单的函数画图。
• 在 3D 图上拖动鼠标转动，按住 Ctrl 拖动鼠标放大缩小，按住 Shift 拖动鼠标平移。

画图综合示例

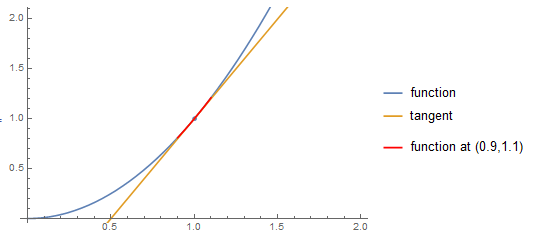
Show[ListPlot[{{1, 1}}],
 Plot[{x^2, 2 x - 1}, {x, 0, 2},
  PlotLegends -> {"function", "tangent"}],
 Plot[x^2, {x, 0.9, 1.1}, PlotStyle -> Red, 
  PlotLegends -> {"function at (0.9,1.1)"}]]

Show[ListPlot[{{1, 1}}], Plot[I^-3 BesselJ[3, I x], {x, 0, 10}], 
 Plot[BesselI[3, x], {x, 0, 10}, PlotStyle -> {Orange, Dashed}], 
 PlotRange -> {{0, 10}, {0, 800}}]

10. 字符串

• 双引号表示字符串，<> 合并两个字符串，相当于 StringJoin["s1", "s2", ...] 或者 StringJoin[{"s1", "s2"}, "s3", ...]，所有的 list 都会被无视
• escape 的规则和 C 语言类似，引号是 \"，反斜杠是 \\，换行符 \n 等。
• 一些系统定义的字符串以 $ 开头，例如 $UserBaseDirectory 表示用户路径，更多详见 “Mathematica 文件操作”。
• StringLength[] 用于检查字符串长度

11. 文件读写

• 从 csv 表格文件读取矩阵如 A = Import["C:\\Users\\abcd\\Desktop\\data.csv", "csv"]。
• Matlab 输出矩阵文件如 writematrix(m,'data.csv')，这样就可以用 Mathematica 读取 Matlab 的数据了。
• Directory[] 输出当前目录，当前目录默认是 $InitialDirectory，Windows 中就是 Documents 文件夹
• SetDirectory[] 设置当前目录。
• Put[表达式1, 表达式2, "文件名"] 可以把表达式存入文件，如果不指定目录，则输出到当前目录
• Save 和 Get 的例子：a = "This must be saved"; fun[x_, y_] := {x, y}; Save["temp", {a, fun}]; Clear[a, fun]; Get["temp"]; 注意多次对同一个文件用 Save 不会覆盖之前的内容，直接把新内容添加到底部。
• Put，DumpSave，Export 研究一下。

12. 程序包

　　 若你需要定义一些经常在不同脚本中使用的函数，你可以创建自己的程序包。创建一个脚本文件

(* ::Package:: *)
BeginPackage["MyPackage`"]
MyFunction::usage = "MyFunction[x] computes the square of x.";
MyFunction[x_] := x^2
Begin["`Private`"]
MyPrivateFunction[x_] := x^3
End[]
EndPackage[]

现在，在其他脚本或者 notebook 中，就可以首先添加 MyPackage.m 所在的路径，然后加载模块，并调用其中的函数

AppendTo[$Path, "C:\\Users\\addis\\Desktop\\"];
Needs["MyPackage`"];

MyFunction[2] (*既可以直接使用函数名*)
MyPackage`MyFunction[3] (*也可以在函数名前面指定包的名字，避免函数名冲突*)

13. “突然不能用” 的错误修复

　　 如果 MMA 某天突然卡在这个界面：

　　 或者出现以下的问题：

• 几乎所有代码都无法正常运行，例如 1+1 也会返回一个错误的结果或干脆一直运行没有返回结果。
• 在执行正确的代码时出现莫名其妙的警告。
• 无法正常打开，例如刚才提到的情况。

　　 这种 bug 貌似是由于 Paclet 没有正确运行或更新导致的。大部分情况下可以参考官方的这个链接进行修复，一般将这个过程称之为 “clean start”：

　　 https://support.wolfram.com/zh/12464

　　 另一种可能的修复方法是：在路径 %APPDATA%\Mathematica\Paclets\Configuration 中找到 pacletSiteData_10.pmd2 这文件并将其删除。

　　 对于 “初始化内核链接...” 卡住的问题，如果上述方法没有成功修复，可以考虑卸载重装。遵照以下官方链接，保证卸载干净：

　　 https://support.wolfram.com/12473