饱和蒸汽压

贡献者： ACertainUser; addis

预备知识 1　理想气体状态方程

　　¹在一定的温度下，若容器中只含有某种液体和它的蒸汽，且达到平衡，这时气体的压强就是饱和蒸汽压。注意饱和蒸汽压只和液体的种类和温度有关。

图 1：水的饱和蒸汽压，横坐标是摄氏温度，纵坐标是毫米汞柱（图片来自维基百科）

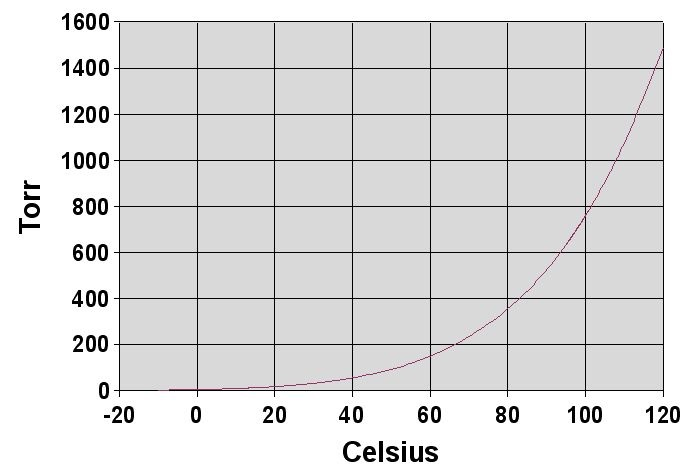
　　我们用一个函数 $P_\alpha(T)$ 描述饱和蒸汽压和温度的关系。例如水蒸气的饱和蒸汽压记为 $P_{H2O}(T)$（图 1 ）。若容器的体积可以变化，当容器变大而温度不变时，压强首先会变小，但液体会继续汽化，直到压强恢复到饱和蒸汽压时重新达到平衡。反之，当容器体积变小（温度不变），则压强首先升高，然后气体会逐渐液化直到恢复饱和蒸汽压时重新达到平衡。一般来说，温度升高会导致饱和蒸汽压升高。

饱和蒸汽的密度

　　为了方便讨论，我们以下假设蒸汽为理想气体。在常温常压（或更低温低压）下这一般是近似成立的，但在高温高压下假设会失效。将饱和蒸汽压代入理想气体状态方程会发现饱和蒸汽的分子密度只与温度有关

\begin{equation} \frac{n_\alpha}{V} = \frac{P_\alpha(T)}{R T}~. \end{equation}

习题 1　水蒸气的质量

　　求 $25^\circ \,\mathrm{C} $ 时一立方米饱和水蒸气的质量。

1. 饱和蒸气压的物理含义

朴素的理解

　　根据热力学第二定律，我们朴素地认为系统的平衡状态兼顾了能量最低与熵最高。例如，在一个只包括水的密闭系统中，如果系统中的水均以液态形式存在，那么系统的能量最低，但是液体比气体有序，熵不高；而如果系统中的水均以气态形式存在，那么系统的熵很高，但能量也太高。因此，只有当系统中的水一部分以气态形式存在、另一部分以液态形式存在时，系统才能兼顾能量最低与熵最高。这就是饱和蒸汽的来历。

　　根据 Schroeder²的说法，熵才是背后的真正驱动力。假如一个过程后系统能量降低、但（系统与环境的）总熵未升高，这样的过程也是不可能的。

热力学证明

预备知识 2　相变平衡条件，相变的热力学量变化

　　假设一个大气压与一定温度下，液态水与水蒸气达到平衡，此时水的蒸气压即为饱和蒸气压 $p^*$。由相变平衡条件，水蒸气的化学势应该等于液态水的化学势。我们以上说的 “熵最高” 原则，已经蕴含在 “相变平衡条件” 所给出的化学势条件中。 $$ \mu_g = \mu_l~, $$ 水蒸气的化学势与水蒸气的分压，即饱和蒸气压有关 $$ \mu_g= \mu_g^\ominus(T,p^\ominus) + RT \ln \frac{p^*}{p^\ominus}~, $$ 液态水受一个大气压，处于标准状态。 $$ \mu_l = \mu_l^\ominus~, $$ 水蒸气的化学势与水的化学势由摩尔相变 Gibbs 变联系 $$ \mu_g^\ominus = \mu_l^\ominus + \Delta_l^g G_m^\ominus~, $$ 综合以上四式， $$p^* = p^\ominus e^{-\frac{\Delta_l^g G_m^\ominus}{RT}}~.$$

　　 $p^*$ 即为该温度下水的饱和蒸气压。$\ominus$ 上标代表我们选取的标准状态，物理化学上可以取 $p^\ominus = 1 \,\mathrm{atm} = 101325 \,\mathrm{Pa} $。有些手册取 $p^\ominus = 100000 \,\mathrm{Pa} $。

2. 混合气体

预备知识 3　理想气体分压定律

　　我们接下来讨论容器中除了某种液体及其蒸汽外，还有另一种气体的情况。以水，水蒸气和干燥的空气³为例。如果将两种气体都视为理想气体，那么两种气体的总压强可以根据分压定律来计算，即水蒸气单独存在时的压强加上空气单独存在时的压强。另外，假设空气分子不溶于水且不与水分子发生任何反应，则水蒸气的分压仍然是 $P_{H2O}(T)$。各种气体的分子密度仍然可以用式 1 计算。

　　令干燥空气的分压为 $P_{air}$ 则混合气体总压强 $P$ 为

\begin{equation} P(T) = P_{H2O}(T) + P_{air}(T)~, \end{equation}

所以若已知总压强和温度，根据式 1 可以计算平衡时两种气体的比例为

\begin{equation} \frac{n_{H20}}{n_{air}} = \frac{P_{H2O}}{P_{air}} = \frac{P_{H2O}(T)}{P - P_{H2O}(T)}~. \end{equation}

3. 绝对湿度和相对湿度

　　我们下面来介绍日常生活中经常使用的相对湿度。我们先定义绝对湿度为 $n'_{H2O}/n'_{air}$ 或者 $P'_{H2O}/P'_{air}$，这里使用一瞥表示实际上的比例而不是平衡时的比例（式 3 ）。若 $P$ 表示大气压强，那么式 3 就是某温度和汽压下可能出现的最大绝对湿度。因为如果实际湿度稍高于这个值，空气中的水蒸气就会迅速凝结到空气中的尘埃上，形成云或雾，有或者直接凝结到物体表面形成水滴或霜。

　　另一方面，空气中绝对湿度常常低于式 3 的值，即水和水蒸气处于不平衡的状态。这是因为地表的水（江湖海，土壤等）蒸发的速度有限，且大气并不是长期处于恒温恒压状态。

　　我们把相对湿度定义为水蒸气的分子实际密度（或分压）除以当前温度下饱和水蒸气的分子密度（或分压）。即

\begin{equation} \phi = \frac{n'_{H2O}}{n_{H2O}} = \frac{P'_{H2O}}{P_{H2O}}~. \end{equation}

4. 沸腾

　　在式 3 中，如果我们实时调节容器的体积，使容器中的气体始终保持某个固定的压强 $P$，那么当温度不断升高时，绝对湿度也会不断升高。当 $P_{H2O}(T)$ 趋近 $P$ 时，容器里面就几乎只有水蒸气了。此时如果温度继续升高使 $P_{H2O}(T)$ 等于或略大于 $P$，系统就无法保持平衡，水会不断汽化，使容器不断膨胀，直到所有的水都变为水蒸气为止。我们把这个过程叫做沸腾（boiling），并定义满足

\begin{equation} P_{H2O}(T_b) = P~ \end{equation}

的温度 $T_b$ 为沸点（boiling point）。沸点与液体的种类以及压强有关。

1. ^ 参考 Wikipedia 相关页面。
2. ^ 参考 Schroeder 的《热物理学导论》
3. ^ 虽然空气由不同种类的分子构成，但容易证明在以下讨论中，是否把空气看成一种分子结论都一样。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。