热力学第二定律

                     

贡献者： ACertainUser; int256; _Eden_; addis

  • 本文处于草稿阶段。
预备知识　熵，卡诺热机

　　 虽然许多基本物理规律（比如牛顿定律，麦克斯韦方程）是可逆的，但许多唯象定律（比如摩擦，传热方程，扩散方程）是不可逆的。克劳修斯首先看出，有必要在热力学第一定律之外建立一条独立的定律来概括自然界的不可逆现象。

1. 被动表述

　　 开尔文表述：不可能从单一热源吸热做功而无环境影响。

　　 克劳修斯表述：热量不能从低温传到高温而无环境影响。

　　 奥斯特瓦德表述：不存在第二类永动机。

　　 可以利用卡诺热机证明，这三种表述是等价的。

未完成：证明等价性

2. 数学表述——卡诺定理

　　 在相同的高温热源和相同的低温热源之间工作的一切可逆热机的效率都相等，与工作物质无关；在相同的高温热源和相同的低温热源之间工作的一切不可逆热机的效率 $\eta'$ 都小于可逆热机的效率 $\eta$：

\begin{equation} \eta'=1-\frac{Q_2'}{Q_1}\le 1-\frac{T_2}{T_1}=\eta~. \end{equation}

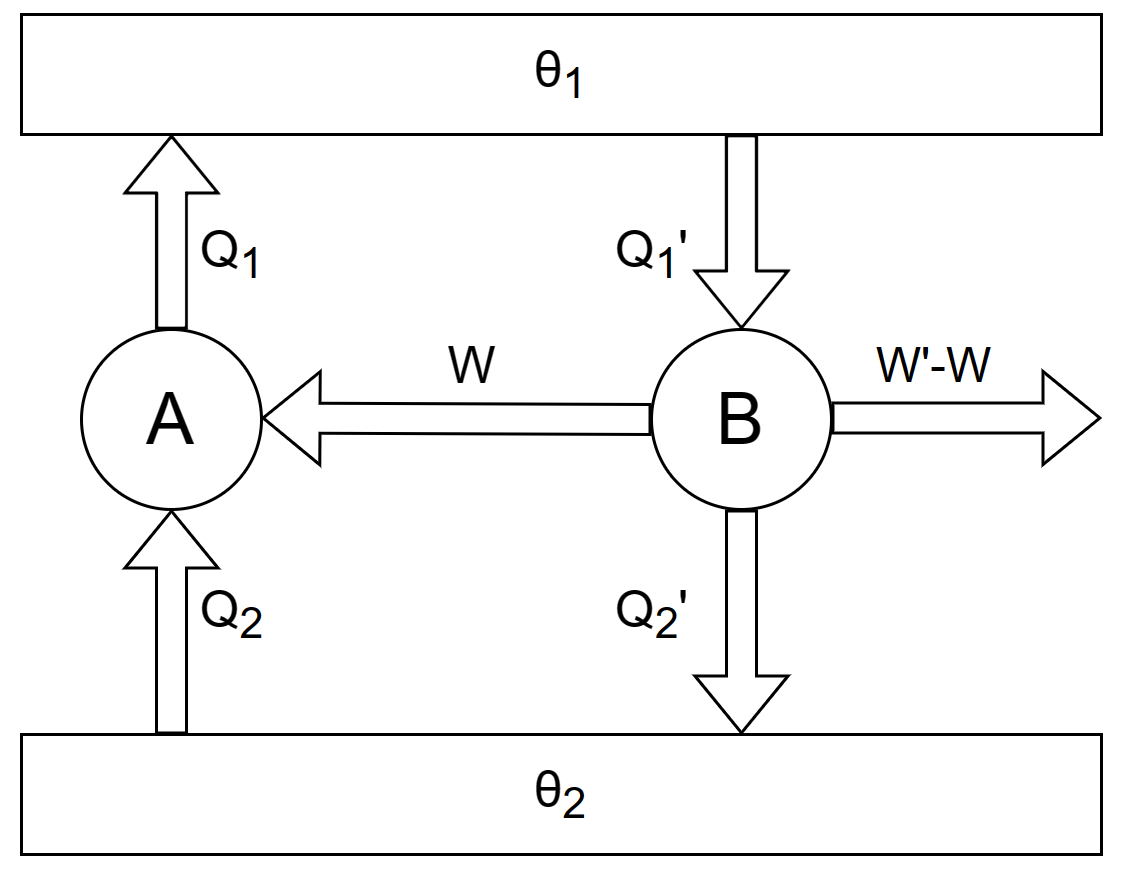
　　 可以由开尔文表述出发，反证卡诺定理。 考虑有一高温热源 $\theta_1$ 与低温热源 $\theta_2$，两个热机 $A$、$B$ 工作其间，分别从高温热源 $\theta_1$ 吸收 $Q_1$ 与 $Q_1'$ 的热量、向低温热源 $\theta_2$ 放出 $Q_2$ 与 $Q_2'$ 的热量。热机 $A$ 对外做功 $W$、热机 $B$ 对外做功 $W'$。

图
图 1：热机 $A$ 与 $B$

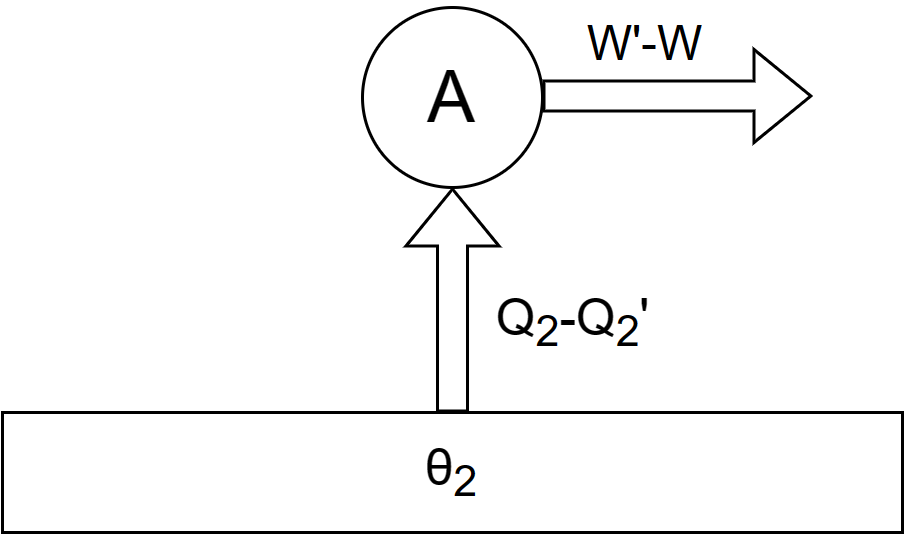
　　 那么热机 $A$ 的效率为 $\eta_A = \frac{W}{Q_1}$，热机 $B$ 的效率为 $\eta_B = \frac{W'}{Q_1'}$。 设 $A$ 为可逆热机，则卡诺定理可以表述为：$\eta_A \ge \eta_B$。由于采用反证法，为此，设 $\eta_A < \eta_B$。也即有 $\frac{W}{Q_1}<\frac{W'}{Q_1'}$。令 $Q_1=Q_1'$，则 $W< W'$，那么可以让 $B$ 热机输出的功的一部分 $W$ 推动热机 $A$ 逆向运行，从低温热源 $\theta_2$ 吸收热量 $Q_2$，运行后输出 $Q_1=Q_1'$ 热量到高温热源 $\theta_1$。此时热机 $B$ 还有多余的功 $W'-W$ 可以输出。等价于下图：

图
图 2：等价热机

　　 根据热力学第一定律，$W'=Q_1'-Q_2'$、$W=Q_1-Q_2'$，故 $$W'-W=Q_2-Q_2' ~.$$ 当 $A$、$B$ 两热机按上述方式一起运行，$A$ 和 $B$ 都是循环过程，均恢复原状；高温热源 $\theta_1$ 也恢复原状；仅仅从低温热源 $\theta_2$ 吸收了 $Q_2-Q_2'$ 的热量并转化为了 $W'-W$ 的有用功，且 $W'-W=Q_2-Q_2'$，是完全转化了的，但没有产生其他影响。这违背开尔文表述：不可能从单一热源吸热做功而无环境影响。所以假设不成立，应当有 $\eta_A \ge \eta_B$。并且可以立刻得到下面推论。

推论 1　所有可逆卡诺热机效率都相等

　　 仍考虑刚才的两热机 $A$、$B$，设其效率分别为 $\eta_A$、$\eta_B$。根据卡诺定理，必定有 $\eta_A \ge \eta_B$ 且 $\eta_B \ge \eta_A$，所以 $\eta_A = \eta_B$，即两热机效率相等。

　　 这反过来也成立，当卡诺定理的不等式取等号时，两热机均为可逆卡诺热机。

3. 克劳修斯不等式；熵的表述

　　1

定理 1　克劳修斯不等式

\begin{equation} \oint \frac{\delta Q}{T} \leq 0 ~, \end{equation}

定理 2　热力学第二定律

　　 封闭系统任意过程前后，总有

\begin{equation} \Delta S \ge \int \frac{\delta q}{T}~, \end{equation}
否则该过程不可能发生。过程可逆时取等号。

　　 热力学第二定律在能量守恒之外设置了额外的（更晦涩难懂）约束条件：有些过程虽然满足能量守恒，但也是不可能发生的。

　　 做一个简单的类比：根据热力学第一定律，如果某个过程前后 $\Delta U \ne \delta q - \delta w$，那么我们知道这个过程是不可能的。同样地，我们说如果某个过程前后 $\Delta S < \int \frac{\delta q}{T}$，那么这个过程同样是不可能的。

4. 应用热力学第二定律：孤立系统

　　 热力学第二定律十足令人费解，因为它涉及一个陌生的物理量熵，还是一个烦人的不等式。为了简化问题，我们先探讨孤立系统（孤立系统不与外界交换热量）中的热力学第二定律。

推论 2　熵增原理

　　 对于绝热或孤立系统，任意过程前后，均有 $Q=0$，因此总有 $$\Delta S \ge 0~,$$ 即绝热或孤立系统的熵永不减少。

　　 我们再试图以不同的形式复读这个定理以明晰他的含义。

推论 3　方向判据

图
图 3：方向判据

　　 如果某一过程后，孤立系统的熵继续升高（至少不降低），那么这个过程可能发生。可见，热力学第二定律的不等号体现了过程的方向性。

推论 4　平衡判据

图
图 4：平衡判据

　　 假如任意过程都不能继续升高系统的熵，那么系统达到平衡状态。从这个定理可以看出，孤立系统热平衡的判据可以设为：熵取极大值。 $$\text{系统平衡} \Leftrightarrow \text{系统熵达到极大} S=S_{extremum} \Leftrightarrow \delta S = 0~.$$

定理 3　热动平衡判据

　　 基于平衡判据与数学推导，我们发现平衡的孤立系统中温度、压强与化学势（如果你还不知道什么是化学势，不用担心，你以后会知道的）处处相同，此谓热动平衡判据。具体的推导参考 “热动平衡判据” 与 “相变平衡条件 ”。 $$ \text{系统平衡} \Rightarrow \delta S = 0 \Rightarrow \left \{ \begin{aligned} T_1 = T_2 = ...\\ p_1 = p_2 = ...\\ \mu_1 = \mu_2 = ...\\ \end{aligned} \right. ~. $$

例 1　为什么需要冰箱

图
图 5：水会自发分成温度不同的两部分吗？

　　 你的桌子上有一杯温度为 $T$ 的水。假设水不与外界交换热量，这杯水会自发分为两部分，使一半杯的温度升为 $T+\Delta T$、而另一半杯的温度降为 $T-\Delta T$ 吗？这样你就不需要冰箱而能同时喝到冷饮与热饮了。

　　 升温部分的熵变 $\Delta S_1=C_p \ln \frac{T+\Delta T}{T}$, 降温部分 的熵变 $\Delta S_2=C_p \ln \frac{T-\Delta T}{T}$

　　 总熵变 $\Delta S = C_p \ln \frac{T+\Delta T}{T} + C_p \ln \frac{T-\Delta T}{T} = C_p \ln \frac{(T+\Delta T)(T-\Delta T)}{T^2}= C_p \ln \frac{T^2 - (\Delta T)^2}{T^2}<0~.$

　　 这违反熵增原理，因此是不可行的。不过反过来说，这解释了为什么两杯温度不同的水混合后，他们的温度将会趋于一致。

5. 应用热力学第二定律：等温等容与等温等压系统

　　2 太长不看：亥姆霍兹自由能与吉布斯自由能。

自由能与自由能判据

　　 在等温等容与等温等压系统中，有很多基于热力学第二定律的简化判据。此处简要讨论一种笔者最喜欢的方法，因为它完全基于上述的讨论。

图
图 6：将系统 $sys$ 与环境 $env$ 视为一个“大系统 $tot$”

　　 为了进一步论证，我们还需先引入一个震撼、可疑又平凡的假设：如果将系统 $sys$ 与环境 $env$ 再视为一个 “大系统 $tot$”，那么这个大系统是孤立系统，因为不存在更大的环境与之交换热或功。同时，这个大系统有能量守恒 $\Delta U_{tot} = \Delta U_{sys} + \Delta U_{env} = 0$。

　　 我们先探讨等温等容系统（系统与环境温度时时相同，但环境与系统只交换热、不做功 $\Delta U = \delta q$, $\Delta S = \delta q / T$），并假定过程可逆，分析大系统的熵增：

\begin{equation} \begin{aligned} \Delta {S_{tot}} &=\Delta {S_{sys}}+\Delta {S_{env}}\\ & =\Delta {S_{sys}}+ \frac{\Delta U_{{env}}}{T}\\ & = \Delta {S_{sys}} - \frac{\Delta U_{{sys}}}{T} \quad \text{能量守恒}~.\\ \end{aligned} \end{equation}
现在，大系统的 $\Delta {S_{tot}}$ 只与原先的系统有关，因此省略 $sys$ 下标。
\begin{equation} \begin{aligned} \Delta {S_{tot}} & = \frac{1}{T}(T \Delta {S} -\Delta U )\\ & = - \frac{1}{T}(\Delta U - T \Delta {S} )~,\\ \end{aligned} \end{equation}
定义 $F = U-TS$，那么 $\Delta F = \Delta U - T \Delta S$，因此有
\begin{equation} \Delta S_{tot} = -\frac{\Delta F}{T}~. \end{equation}

　　 对大系统运用孤立系统的熵判据，发现

\begin{equation} \Delta S_{tot} > 0\Rightarrow \Delta F < 0~. \end{equation}

　　 也就是说，如果某个过程后 $\Delta F < 0$，那么它可以发生。这就是亥姆霍兹自由能 与 亥姆霍兹判据。可见，对于非绝热系统，尽管系统自身的熵可以降低，但是系统和环境一起的 “大系统” 的总熵必须增加。

　　 类似地，对于等温等压系统，我们有吉布斯自由能 与相应的 Gibbs 判据。

热二与系统做功能力

　　 接下来，我们探讨热二如何影响系统的做功能力。我们假定一个封闭等温等容的系统。根据热一 的能量守恒，我们有 $$\Delta U = q - w_{\text{非体}} \Rightarrow w_{\text{非体}} = q - \Delta U ~,$$ 功可以被分为体积功与非体积功 $w = w_\text{体}+w_\text{非体}$，体积功指因为系统体积变化而导致的机械功 $w_\text{体}=p\Delta V$，而非体积功指其余类型的功 $w_\text{非体}$，例如电功等。此处由于等容，系统不做体积功 $w_\text{体} = 0$。

　　 同时，根据热二我们有 $$ \Delta S \ge \frac{q}{T} \Rightarrow q \le T \Delta S~. $$

　　 我们假定系统发生一个放能过程 $\Delta U < 0$，并且分类讨论 $\Delta S$.

  1. $\Delta S > 0$，那么热二的 $q \le T\Delta S$ 允许 $q$ 是一个正值，即热流入系统。根据之前的论述， $$ w_\text{非体} = q - \Delta U \ge - \Delta U ~, $$ 别忘了，$\Delta U<0$，那么 $-\Delta U>0$。这种情况下，系统能够从外界吸收热并将其转换为非体积功！这与我们对热二 “效率上限” 的粗浅理解似乎有一些矛盾。这表明我们应该谨慎地处理热二问题，而不能一言以蔽之。虽然系统把热转换为了功，但是代价却是自己的熵增高了。从这角度上讲，可以理解为什么有人把熵称为 “系统的寿命”：做功得牺牲系统的阳寿。3
  2. $\Delta S < 0$，那么 $q \le T\Delta S < 0$，$q$ 只能是负值，即热流出系统。同样， $$ w_\text{非体} = q - \Delta U \le - \Delta U ~, $$ 这表明这种情况下系统不得不以热的形式排出一部分能量，而不能将其完全转换为功。这或许才是我们想象中的热二。

自由能的物理含义

　　 在上文中，我们知道了 $$ w_{\text{非体}} = q - \Delta U~.$$ 直接代入热二的 $$ q \le T\Delta S ~, $$ 我们得到了一个有趣的不等式： $$ w_{\text{非体}} = q - \Delta U \le T \Delta S - \Delta U = - (\Delta U-T \Delta S ) ~, $$ 等号右边的竟然就是我们之前引入的 $\Delta F$!(差一个负号)

\begin{equation} w_\text{非体} \le - \Delta F~, \end{equation}
因此，对于一个等温等容过程，$-\Delta F$ 的数值含义是过程后系统能对外做的最多的非体积功。因此，我们常说，自由能度量了系统做非体积功的能力。同时，我们更深刻明白了，热一与热二如何共同约束系统的变化：
\begin{equation} \left \{ \begin{aligned} \Delta U &= q-w\\ \Delta S &\ge \frac{q}{T}\\ \end{aligned} \right.~. \end{equation}

习题 1　

　　 同理，论证 Gibbs 自由能变 $\Delta G$ 在等温等压系统中的含义。

6. 熵增原理与热力学第二定律的微观解释

图
图 7：热力学第二定律的微观含义：系统最有可能处于具有最多微观态个数的分布

　　 由于热力学熵和玻尔兹曼熵之间的关系（在热力学极限 $N\rightarrow \infty$ 下，宏观熵 $=$ 微观熵），热力学第二定律有其统计意义：孤立系统的自发过程总是从有序向无序过渡，即从微观状态数小的宏观状态向微观状态数大的宏观状态过渡，该过程因此是不可逆的。也就是说，虽然基本物理定律是有时间反演不变性，但从统计意义上看，宏观规律却能体现时间箭头的方向！

　　 且由此我们可以知道孤立系统处于平衡态时它的熵一定是处于极大值的，否则系统就会自发地朝熵增大的方向演化。这就是孤立系统处于平衡态的熵判据，具体内容可以参考热动平衡判据文章。

1. ^ 下文参考自朱文涛《简明物理化学》与邹远川的《热力学与统计力学》课程。
2. ^ 本节的证明方法参考了 Schroeder 的《热物理学导论》。这也是一种常规的方法。Schroeder 对于自由能有一些非常精辟的表述，我把这个惊喜留给你自己去读
3. ^ 好奇的小伙伴可能会问，“系统吸热做功” 会不会和 “不可能从单一热源吸热做功而无环境影响” 的论述矛盾？事实上是不会的，“影响” 就是系统的熵增高了。随着系统的熵增加到极值，这样的过程就不可继续发生了，相当于系统用尽了阳寿。类比电池，相当于电池用着用着就用没电了、也就不能再放电。


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利