贡献者: JierPeter; addis; _Eden_
约定采用自然单位制,即 $c=1$。
不论是牛顿力学框架下还是相对论意义下,光的频率都可能在不同参考系之间有所不同。由于观察者和光源之间相对运动,造成观察者所测得的光的频率与光源的频率不一致,这个现象被称为光的多普勒效应。由于光速不变原理,在相对论框架下讨论光的多普勒效应反而更为简单。
1. 光的多普勒效应的推导
由于在任何参考系中,光的速度都一样,因此只需要知道光的波长就可以根据以下公式得到光的频率:
\begin{equation}
f=\frac{1}{\lambda}~.
\end{equation}
其中,$f$ 是光的频率,$\lambda$ 是光的波长,$1$ 是光速。
假设光源所在的参考系为 $K_1$,观察者所在的参考系为 $K_2$,而 $K_2$ 相对 $K_1$ 的运动速度为 $\vec{v}=(v, 0, 0)^T$。设光的频率在 $K_1$ 为 $f$,在 $K_2$ 中为 $f'$,那么光的波长在 $K_1$ 中为 $\lambda=1/f$,在 $K_2$ 中为 $\lambda'=1/f'$。
一维情况
设在 $K_1$ 看来,观察者和光的运动方向是一致的,即观测者以 $v$ 的速度背离光源运动。
取 $K_1$ 中光的两个相邻的波峰1,作为两个以光速运动的点。为简化讨论,不妨设其中一个点的世界线2表示为
\begin{equation}
\begin{pmatrix}t_1\\t_1\\0\\0\end{pmatrix} ~,
\end{equation}
而另一个点为
\begin{equation}
\begin{pmatrix}t_2\\t_2+\lambda\\0\\0\end{pmatrix} ~.
\end{equation}
代入洛伦兹变换可得,在 $K_2$ 中两波峰的世界线分别为
\begin{equation}
\begin{pmatrix}\frac{t_1-vt_1}{\sqrt{1-v^2}}\\\frac{t_1-vt_1}{\sqrt{1-v^2}}\\0\\0\end{pmatrix} ~,
\end{equation}
和
\begin{equation}
\begin{pmatrix}\frac{t_2-v(t_2+\lambda)}{\sqrt{1-v^2}}\\\frac{(t_2+\lambda)-vt_2}{\sqrt{1-v^2}}\\0\\0\end{pmatrix} = \begin{pmatrix}\frac{t_2-vt_2-v\lambda}{\sqrt{1-v^2}}\\\frac{t_2-vt_2+\lambda}{\sqrt{1-v^2}}\\0\\0\end{pmatrix} ~.
\end{equation}
在各参考系中计算波长,就要计算对应参考系中同一时间下两波峰的空间坐标的差。对于 $K_1$,“同一时间” 意味着 $t_1=t_2$;对于 $K_2$,“同一时间” 意味着 $t_1-vt_1=t_2-v(t_2+\lambda)$,
将 “同一时间” 条件分别代入两个参考系中两个点的世界线,消去 $t_1$ 计算后发现,两波峰在 $K_1$ 中的距离始终是 $\lambda$,而在 $K_2$ 中的距离始终是 $\frac{(1+v)\lambda}{\sqrt{1-v^2}}$。由于已经设定这束光在 $K_2$ 中的波长是 $\lambda'$,因此有
\begin{equation}
\lambda'=\frac{(1+v)\lambda}{\sqrt{1-v^2}}=\frac{\sqrt{1+v}}{\sqrt{1-v}}\lambda~.
\end{equation}
因此在 $K_2$ 中,光的频率变为
\begin{equation}
f'=\frac{1}{\lambda'}=\frac{\sqrt{1-v}}{\sqrt{1+v}\lambda}=\frac{\sqrt{1-v}}{\sqrt{1+v}}f~.
\end{equation}
这就是一维情况下光的多普勒效应。对于背离光源运动的观测者来说,光的频率发生了红移($f'< f$)。
三维情况
三维情况下,可以预料在 $K_1$ 看来光的传播方向和在 $K_2$ 参考系看来的运动方向不一致的情况。因此情况会较为复杂,我们需要考虑新的方法。
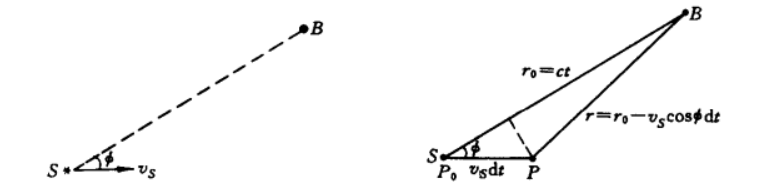
考察图 1 的情况,我们直接在$K_2$ 参考系中进行分析,不妨假设光源 $S$ 正以 $v$ 的速度沿 $x$ 轴正方向运动,并且在 $K_2$ 参考系看来在 $t$ 时刻接收到的电磁波方向与 $x$ 轴成 $\phi$ 角(注意这个角度是在 $K_2$ 参考系测得的)。
图 1:多普勒效应示意图(参考舒幼生力学
[1] 8.3.2 节例 11 的图)
假设在 $0$ 时刻光源位于 $P_0$ 点,它发出的电磁波于 $t$ 时刻被 $B$ 点处的观测者接收到,并且观测者测得的电磁波方向与 $x$ 轴夹角为 $\phi$。那么 $S$ 到 $B$ 的距离为 $r_0=ct=t$(自然单位制下 $c=1$)。而经过 $ \,\mathrm{d}{t} $ 的时间后光源移动到了 $P$ 点的位置,在这段时间内光源所经历的固有时(也就是 $K_1$ 参考系中光源所经历的原时)为 $ \,\mathrm{d}{t} /\gamma=\sqrt{1-v^2} \,\mathrm{d}{t} $(即钟慢效应),因此在这段时间内光源 “振动” 的次数为
\begin{equation}
N'=f\cdot \gamma \,\mathrm{d}{t} = f\sqrt{1-v^2} \,\mathrm{d}{t} ~,
\end{equation}
现在考虑光源在 $P$ 点处发出的电磁波在什么时刻被 $B$ 点接受到。如图所示,$P$ 到 $B$ 的距离为
\begin{equation}
r=r_0-v\cos\phi \,\mathrm{d}{t} =t-v\cos\phi \,\mathrm{d}{t} ~,
\end{equation}
这也就意味着光源从 $P$ 发出的电磁波经过了 $r/c=r$(自然单位制下 $c=1$)的时间被 $B$ 点的观测者接收到。经过计算,可以看到 $P_0$ 点发出的电磁波与 $P$ 点发出的电磁波被 $B$ 点观测者接收到的时间差为
\begin{equation}
\,\mathrm{d}{t} ' = \,\mathrm{d}{t} + r - t = \,\mathrm{d}{t} -v\cos\phi \,\mathrm{d}{t} ~.
\end{equation}
因此根据
式 8 和
式 10 ,$K_2$ 参考系中 $B$ 点观测者观测到的光的频率为
\begin{equation}
f'=\frac{N'}{ \,\mathrm{d}{t} '}=\frac{\sqrt{1-v^2}}{1-v\cos\phi} f~.
\end{equation}
这就是三维空间中一般情况下光的多普勒效应。如果 $\phi=0$ 或 $\phi=\pi$,那么情况退化为一维空间的问题。作为验证将 $\phi=\pi$ 代入式 11 后结果和式 7 一致,这种情况对应于光源背离观测者运动(或观测者背离光源运动)的情况。
另一个更具数学技巧和简洁性的推导是利用了波四矢 $k^\mu$ 的变换规则,具体过程见狭义相对论运动学(无质量粒子)。
1. ^ 也可以是相邻波谷,或者任何相邻的两个同相位的点。
2. ^ 见时空的四维表示或世界线和固有时。
[1] ^ 舒幼生. 力学 第一版
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。