狭义相对论的运动学（无质量粒子和多普勒效应）

贡献者： _Eden_

预备知识　世界线和固有时

　　约定使用东海岸度规 $\eta_{\mu\nu}=\rm{diag}(-1,1,1,1)$ 和自然单位制 $c=\hbar=1$。

1. 四速度、四动量、波四矢量

　　对于无质量粒子，它的世界线为类光世界线，$V^\mu= \,\mathrm{d}{x} ^\mu(\lambda)/ \,\mathrm{d}{\lambda} $ 满足 $V^\mu V_\mu = 0$。我们无法用固有时对类光世界线进行参数化，因为在类光世界线上的任意两点的时空间隔都为 $0$。那么我们只能寻求其他的参数化方式。在狭义相对论中，无质量粒子不会受到力的作用，因此其四速度是恒定的，世界线在时空中是一条直线。例如以下就是一条无质量粒子的世界线：

\begin{equation} x^\mu(\lambda)=b^\mu \lambda,\quad b^\mu=(1,1,0,0)~, \end{equation}

容易验证 $V^\mu=(1,1,0,0)$ 满足 $V^\mu V_\mu = 0$。

　　无质量粒子的能量与波的频率 $\omega$ 成正比，动量与波数 $ \boldsymbol{\mathbf{k}} $ 成正比，即德布罗意关系。那么可以定义其四动量为

\begin{equation} p^\mu=(E, \boldsymbol{\mathbf{P}} )=(\hbar \omega,\hbar \boldsymbol{\mathbf{k}} )=\hbar k^\mu~, \end{equation}

$\hbar$ 为约化普朗克常数。在自然单位制下，$p^\mu=(E, \boldsymbol{\mathbf{P}} )=(\omega, \boldsymbol{\mathbf{k}} )=k^\mu$。四动量方向应当与四速度方向一致，即

\begin{equation} \hat p,\hat k \propto \hat V= \frac{\mathrm{d}{\hat x(\lambda)}}{\mathrm{d}{\lambda}} ~, \end{equation}

因此它满足爱因斯坦质能关系

\begin{equation} p^\mu p_\mu = E^2-| \boldsymbol{\mathbf{P}} |^2=\omega^2-| \boldsymbol{\mathbf{k}} |^2=0~. \end{equation}

2. 多普勒效应

　　考虑一个光源，在它的参考系中光子沿各个方向以频率 $\omega$ 发射。而对于接收器，假设它相对于光源以速度 $ \boldsymbol{\mathbf{v}} =-v \hat e_x$ 运动（$v>0$ 代表相向，$v<0$ 代表背向运动）。

　　假设在光源参考系 $S$ 中，以 $\alpha$ 角发射的光子被接收器接收到。那么假设在观测者静止的参考系 $S'$ 中，在观测者眼中光子是以 $\alpha'$ 角接收到的，即观测到的光子具有波四矢量

\begin{equation} k'^\mu = \frac{2\pi}{\lambda'}(1,\cos\alpha',\sin\alpha',0)~, \end{equation}

$\lambda'$ 为参考系 $S'$ 中接收器观测到的光子波长。

　　那么可以通过一个 $ \boldsymbol{\mathbf{v}} $ 方向的洛伦兹变换

\begin{equation} \Lambda^\mu{}_\nu=\begin{pmatrix} \gamma & -v\gamma & & \\ -v\gamma & \gamma & & \\ & & 1 & \\ & & & 1 \end{pmatrix}~. \end{equation}

那么我们希望

\begin{equation} k^\mu = \Lambda^\mu{}_\nu k'^\nu = \frac{2\pi}{\lambda}(1,\cos\alpha,\sin\alpha,0)~, \end{equation}

转化为求解以下方程组

\begin{equation} \begin{aligned} & \gamma\cdot\frac{2\pi}{\lambda'}\left(1-v\cos\alpha'\right)=\frac{2\pi}{\lambda}~,\\ & \gamma\cdot\frac{2\pi}{\lambda'}\left(\cos\alpha'-v\right)=\frac{2\pi}{\lambda}\cos\alpha~,\\ & \frac{2\pi}{\lambda'}\sin\alpha' = \frac{2\pi }{\lambda}\sin\alpha~. \end{aligned} \end{equation}

经过适当的化简最终可以得到

\begin{equation} \begin{aligned} &\frac{\lambda'}{\lambda}=\gamma(1-v\cos\alpha')~,\\ &\tan\alpha=\frac{\tan\alpha'}{\gamma(1-v\sec \alpha')}~. \end{aligned} \end{equation}

第一个公式可以换作频率的表达式 $\nu=2\pi/\lambda$：

\begin{equation} \nu'=\frac{\nu}{\gamma(1-v\cos\alpha')}~. \end{equation}

习题 1　

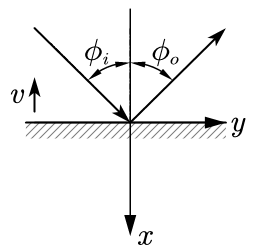
　　一个平面镜沿与镜面垂直的方向以常速度 $v$ 运动。一束频率为 $\nu_i$ 的光以入射角 $\phi_i$ 与镜面发生碰撞，反射角为 $\phi_o$，而反射光子的频率为 $\nu_o$。证明如下关系：

\begin{equation} \frac{\tan\frac{1}{2}\phi_i}{\tan\frac{1}{2}\phi_o}=\frac{1+v}{1-v},\quad \frac{\nu_o}{\nu_i}=\frac{\sin\phi_i}{\sin\phi_o}~. \end{equation}

　　 证明：

图 1：习题 1 示意图

　　设平面镜参考系（相对于实验室参考系以 $v$ 的速度向 $-x$ 方向运动）下入光的波四矢为

\begin{equation} k'_i{}^\mu=\nu'(1,\cos\theta',\sin\theta',0)~. \end{equation}

出射光的波四矢为

\begin{equation} k'_o{}^\mu=\nu'(1,-\cos\theta',\sin\theta',0)~. \end{equation}

那么如果切换到实验室参考系，我们有

\begin{equation} \begin{aligned} k_i&=\Lambda^\mu{}_\nu k'_i{}^\nu=\nu'(\gamma(1-v\cos\theta'),\gamma(\cos\theta'-v),\sin\theta',0)\\ &=\nu_i(1,\cos\phi_i,\sin\phi_i,0)~,\\ k_o&=\Lambda^\mu{}_\nu k'_o{}^\nu=\nu'(\gamma(1+v\cos\theta'),\gamma(-\cos\theta'-v),\sin\theta',0)\\ &=\nu_o(1,-\cos\phi_o,\sin\phi_o,0)~. \end{aligned} \end{equation}

比较 $k_i,k_o$ 的第三个分量，它们应当相等，所以可以得到

\begin{equation} \frac{\nu_o}{\nu_i}=\frac{\sin\phi_i}{\sin\phi_o}~. \end{equation}

再考虑计算 $\frac{ \tan\left(\phi_i/2\right) }{ \tan\left(\phi_o/2\right) }$，利用公式 $ \tan\left(\theta/2\right) =\frac{\sin\theta}{\cos\theta+1}$，可以得到

\begin{equation} \begin{aligned} \tan\left(\theta_i/2\right) &=\frac{\nu_i\sin\theta_i}{\nu_i\cos\theta_i+\nu_i}=\frac{\nu'\sin\theta'}{\nu'\gamma(\cos\theta'-v)+\nu'\gamma(1-v\cos\theta')}\\ &=\frac{\sin\theta'}{\gamma(1-v)(1+\cos\theta')}~. \end{aligned} \end{equation}

同理

\begin{equation} \begin{aligned} \tan\left(\theta_o/2\right) &=\frac{\nu_o\sin\theta_o}{\nu_o\cos\theta_o+\nu_o}=\frac{\nu'\sin\theta'}{\nu'\gamma(\cos\theta'+v)+\nu'\gamma(1+v\cos\theta')}\\ &=\frac{\sin\theta'}{\gamma(1+v)(1+\cos\theta')}~. \end{aligned} \end{equation}

因此我们最终证明了

\begin{equation} \begin{aligned} \frac{\tan\frac{1}{2}\phi_i}{\tan\frac{1}{2}\phi_o}=\frac{1+v}{1-v},\quad \frac{\nu_o}{\nu_i}=\frac{\sin\phi_i}{\sin\phi_o}~. \end{aligned} \end{equation}

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。