贡献者: ACertainUser; addis; JierPeter; Giacomo
1. 一点处的导数
几何含义
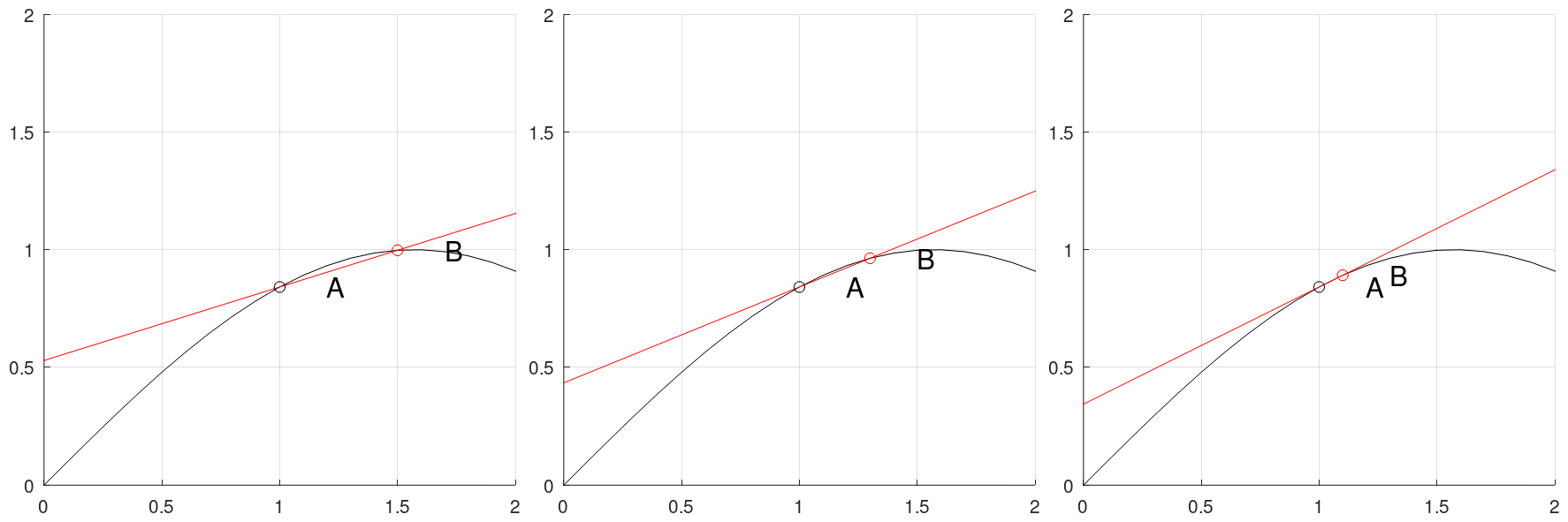
12一个一元函数 $y = f(x)$ 在直角坐标系中表示为一条曲线。在切线与割线中,我们已经初步了解了什么是切线与割线。
图 1:B 趋向 A,割线趋向切线
我们先写出割线的直线方程。由于割线就是一条经过 A,B 两点的直线,根据高中数学知识,很容易得到
\begin{equation}
y-y_A=\frac{y_B-y_A}{x_B-x_A}(x-x_A)=\frac{f(x_B)-f(x_A)}{x_B-x_A}(x-x_A)~.
\end{equation}
观察割线的方程,除了斜率项 $k=\frac{f(x_B)-f(x_A)}{x_B-x_A}$,其余项均与 $x_B$ 无关。现在,如图 1 所示,我们固定 A 点不动,让 B 点趋近于 A 点,即令 $x_B\rightarrow x_A$,这使割线趋向于切线,它的斜率即可用极限来定义
\begin{equation}
k=\lim_{x_B\to x_A}\frac{f(x_B)-f(x_A)}{x_B-x_A}~.
\end{equation}
我们把这个切线的斜率定义为 $x=x_A$ 处 $f(x)$ 的导数,一般记为 $f'(x_A)$ 或 $ \frac{\mathrm{d}{f}}{\mathrm{d}{x}} |_{x=x_A}$。因此,我们说函数一点处的导数值就等于这点处切线的斜率。
图 2:点 $A$ 的切线。$f'(x_A)=k=\tan \theta$
更一般的,有
定义 1 函数一点处的导数
$f(x)$ 在 $x=x_0$ 处的导数为
\begin{equation}
f'(x_0)=\lim_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}~,
\end{equation}
也可以写为
\begin{equation}
f'(x_0)=\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}~.
\end{equation}
“物理” 含义
仔细观察 $x=x_0$ 附近切线的形状与 $f(x)$ 的形状,你很容易看出这两者是几乎一样的3,这启发我们在一个小区域内用切线来近似原函数。
图 3:将切点放大,会发现切线和曲线在切点附近 “重合”
此时,若想计算 $x$ 轻微增加后,函数值 $y$ 的增量,就没有必要复杂地计算
$$\Delta y = f(x_0+\Delta x) - f(x_0)~,$$
而只需要计算
\begin{equation}
\Delta y = f'(x_0) \Delta x~,
\end{equation}
这就引入了
微分的概念。更重要的是,这启发了我们导数的另一层含义:导函数确定了 $x=x_0$ 处,$y$ 关于 $x$ 变化的 “敏感度”,即 $x$ 轻微变化时,$y$ 会做出多大的响应。例如,一个绝对值大的导数值意味着 $y$ 会因为 $x$ 的轻微变化而剧烈变化。
理解这一含义的最直白例子或许是速度,速度被定义为物体位置关于时间的导数 $v= \frac{\mathrm{d}{r}}{\mathrm{d}{t}} $。即使只靠直觉,我们也能理解“速度快” 就是指 “一瞬间他就从我眼前飞过去了”,这就是说当时间轻微增加时,物体的位置大幅变化。
单侧导数
类似于单侧极限,我们也可以引入单侧导数的概念。如果 B 点从右侧趋近 A 点,但始终不运动到 A 点的左侧,那么此时切线的斜率即为该点处函数的右导数值,可以记为 $f'_+(x_A)$。更一般地,用极限的语言可以写为:
定义 2 单侧导数
$f(x)$ 在 $x=x_0$ 处的右导数为:
\begin{equation}
f'_+(x_0) = \lim_{x\to x_0^+} \frac{f(x)-f(x_0)}{x-x_0}~.
\end{equation}
同理,可以定义左导数:
\begin{equation}
f'_-(x_0) = \lim_{x\to x_0^-} \frac{f(x)-f(x_0)}{x-x_0}~.
\end{equation}
类似于极限,我们也有
定理 1
函数在某点可导的充分必要条件是它左右导数都存在并相等。
$$f'(x_0)=A\Longleftrightarrow f'_+(x_0)=f'_-(x_0)=A~.$$
也就是说,若左(或右)导数不存在,或者左、右导数存在但不相等,那此处的导数就不存在。
例 1
如图,在棱角处,虽然函数连续,甚至左、右导数均存在,但他们的大小不相同,因此在棱角处该函数不可导。
图 4:棱角处不可导
一个更明确的例子是绝对值函数 $f(x) = |x|$, 它在零点的左导数为 $-1$,而右导数为 $1$。
未完成:作图:函数图像和导函数图像
。
2. 导函数
在上文中,我们定义了一点处函数的导数。原则上我们可以任意选取函数定义域中的一点,然后用根据上文 “导数的定义” 找到该点处的导数值。这也就是说,对于函数定义域中的任意一点,都有一个导数值与之对应,这符合函数的定义,也就是说我们可以在这二者间定义一个新函数,这就是 $f(x)$ 的 “导函数”;在不引起混淆的情况下往往简称为 “导数”。
字面上看,导函数的定义与一点处函数的导数完全类似。
定义 3 导函数
\begin{equation}
f'(x)=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}~.
\end{equation}
通常将导函数记为以下的一种
\begin{equation}
f'(x),\quad [f(x)]',\quad \frac{\mathrm{d}{y}}{\mathrm{d}{x}} ,\quad \frac{\mathrm{d}{f}}{\mathrm{d}{x}} ,\quad \frac{\mathrm{d}}{\mathrm{d}{x}} f(x)~.
\end{equation}
在物理中,还可以在物理量上方加一点表示对时间求导(注意仅限于对时间求导),例如 $\dot f(t) = \mathrm{d}{f(t)}/\mathrm{d}{t} $。
例 2 直线方程的导函数
计算 $f(x)=2x+3$ 的导函数。
根据定义,
$$
\begin{aligned}
f'(x)&=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\\
&=\lim_{\Delta x \to 0}\frac{[2(x+\Delta x)+3]-(2x+3)}{\Delta x}\\
&=\lim_{\Delta x \to 0}\frac{2\Delta x}{\Delta x}\\
&=2~.
\end{aligned}
$$
事实上,所有直线方程的导函数都是常函数,且数值上等于自己的斜率。当然,实际上很少直接使用定义计算导数,有一些技巧可以简化求导过程(见本节其他文章)。
例 3 常函数的导函数
计算 $f(x)=C$ 的导函数, 其中 $C$ 是常数。
仍然根据定义,
$$
\begin{aligned}
f'(x)&=\lim_{\Delta x \to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}\\
&=\lim_{\Delta x \to 0}\frac{C-C}{\Delta x}\\
&=\lim_{\Delta x \to 0}\frac{0}{\Delta x}\\
&=0~,\\
\end{aligned}
$$
因此常函数的导数为零。这可以理解为例 2 当 $x$ 的系数为零时的特例。
例 4 二次函数的导函数
计算 $f(x)= a x^2 + b x + c$ 的导函数。
仍然根据定义,
$$
\begin{aligned}
f'(x)&=\lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x} \\
&=\lim_{\Delta x \to 0} \frac{a(x + \Delta x)^2 + b (x + \Delta x) + c - a x^2 - b x - c}{\Delta x} \\
&=\lim_{\Delta x \to 0} \frac{2 a x (\Delta x) + a (\Delta x)^2 + b \Delta x}{\Delta x} \\
&=\lim_{\Delta x \to 0} 2 a x + a (\Delta x) + b \\
&= 2 a x + b ~,\\
\end{aligned}
$$
因此二次函数的导数为一次函数。当 $a = 0$,二次函数退化为直线方程。
1. ^ 本文参考了 [1] , [2]
2. ^ 除非特别声明,我们暂且假定探讨的函数在定义域内处处可导,就和大多数物理学家和工程师所默许的一样
3. ^ 这个结论可不是我瞎说的,数学上是能给出严格的证明
[1] ^ 同济大学数学系. 高等数学 (上下册) 高等教育出版社 (2014) 第七版
[2] ^ J. Hass, C. Heil, M. Weir.Thomas' Cauculus 14ed
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。