刚体定轴转动、转动惯量

贡献者： addis; 零穹

预备知识 1　刚体，角动量定理，匀加速直线运动

1. 刚体的定轴转动

　　若刚体绕固定轴转动，那么刚体的位置只需一个变量即可完全确定（一个自由度），我们令该变量为转角 $\theta$。$\theta$ 关于时间 $t$ 的导数就是刚体定轴旋转的角速度 $\omega$。我们还可以定义角速度 $\omega$ 关于时间的导数（即 $\theta$ 关于时间的二阶导数）为角加速度（angular acceleration），记为 $\alpha$

\begin{equation} \alpha = \frac{\mathrm{d}^{2}{\theta}}{\mathrm{d}{t}^{2}} ~. \end{equation}

　　我们可以把刚体的定轴转动类比质点的直线运动，把 $\theta$，$\omega$ 和 $\alpha$ 分别类比为直线运动中的位置 $x$，速度 $v$ 和加速度 $a$，因为后三个变量之间的数学关系是完全相同的：$v, \omega$ 分别是 $x, \theta$ 的一阶导数，而 $a, \alpha$ 分别是 $x, \theta$ 的二阶导数。

　　于是我们可以立即类比匀加速直线运动得到匀变速定轴转动（即 $\alpha$ 为常数）的一些公式，如

\begin{gather} \omega = \omega_0 + \alpha t~,\\ \theta = \theta_0 + \omega_0 t + \frac12 \alpha t^2~,\\ \omega_1^2 - \omega_0^2 = 2\alpha (\theta_1-\theta_0)~. \end{gather}

　　在以上三个标量的基础上，我们可以定义它们的矢量形式 $ \boldsymbol{\mathbf{\theta}} $，$ \boldsymbol{\mathbf{\omega}} $ 和 $ \boldsymbol{\mathbf{\alpha}} $，令它们的方向为转轴的方向，用右手定则来判断。在刚体定轴转动的约束下，三个矢量的方向都是转轴的方向，所以一般用标量就足够了，这就好比讨论质点的直线运动时，用标量表示位置，速度，加速度就够了。只有当转轴会随时间改变时才有必要使用矢量形式（见 “惯性张量”）。

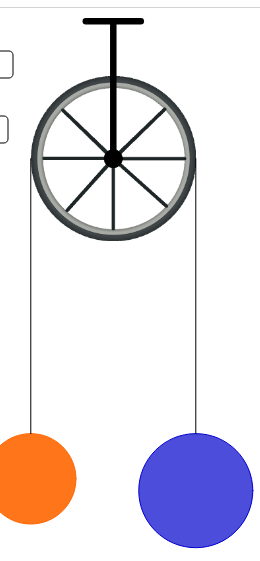
　　要判断刚体上任意一点的速度，使用式 5 即可（见图 1 ）

\begin{equation} \boldsymbol{\mathbf{v}} = \boldsymbol{\mathbf{\omega}} \boldsymbol\times \boldsymbol{\mathbf{r}} = \boldsymbol{\mathbf{\omega}} \boldsymbol\times \boldsymbol{\mathbf{r}} _\bot~. \end{equation}

图 1：刚体定轴旋转时任意一点的线速度

　　以上只是运动学而不含动力学，也就是并没有考虑力和运动之间的关系。下面我们将通过角动量定理得出类似牛顿第二定律的动力学公式：

\begin{equation} \tau_z = I \alpha~, \end{equation}

其中 $\tau_z$ 是外力对系统的合力矩在转轴方向（令为 $z$ 轴）的分量，对应牛顿第二定律中的力 $F$；$I$（有时也用 $J$）是一个和刚体的质量分布有关的量叫转动惯量，对应牛顿第二定律力学中的质量 $m$。

2. 角动量的轴向分量与转动惯量

　　要讨论刚体的定轴转动和所受力矩之间的关系，我们需要先来看角动量矢量在转轴正方向的分量}。以后会知道若定轴旋转的刚体的质量分布关于转轴有某种旋转对称¹，那么刚体的角动量矢量必定是平行于转轴的，然而对于更一般的刚体（如图 1 ），定轴转动时的角动量矢量就未必与转轴平行（如例 1 ）。所以为了简单起见我们先讨论其轴向的分量，完整的矢量关系以后会在 “惯性张量” 中看到。

　　我们把转轴的某个正方向定义为 $z$ 轴正方向，单位矢量记为 $ \hat{\boldsymbol{\mathbf{z}}} $。对于刚体上的单个质点，角动量在 $z$ 方向的分量为

\begin{equation} L'_{z} = \boldsymbol{\mathbf{L}} \boldsymbol\cdot \hat{\boldsymbol{\mathbf{z}}} = ( \boldsymbol{\mathbf{r}} \boldsymbol\times \boldsymbol{\mathbf{p}} ) \boldsymbol\cdot \hat{\boldsymbol{\mathbf{z}}} ~. \end{equation}

首先把质点的位矢在 $z$ 方向和垂直 $z$ 方向分解（称为水平方向），$ \boldsymbol{\mathbf{r}} = \boldsymbol{\mathbf{r}} _z + \boldsymbol{\mathbf{r}} _ \bot$。由于 $ \boldsymbol{\mathbf{p}} $ 一直沿水平方向，根据叉乘的几何定义，$ \boldsymbol{\mathbf{r}} _z \boldsymbol\times \boldsymbol{\mathbf{p}} $ 也是沿水平方向，只有 $ \boldsymbol{\mathbf{r}} _ \bot \boldsymbol\times \boldsymbol{\mathbf{p}} $ 沿 $z$ 方向。另外，在圆周运动中，半径始终与速度垂直，所以 $ \boldsymbol{\mathbf{r}} _ \bot$ 始终与 $ \boldsymbol{\mathbf{p}} $ 垂直。得出结论

\begin{equation} L'_z = \left\lvert \boldsymbol{\mathbf{r}} _\bot \right\rvert \left\lvert \boldsymbol{\mathbf{p}} \right\rvert = m r_ \bot v = mr_ \bot ^2\omega ~. \end{equation}

　　现在讨论刚体的角动量，若把刚体分成无数小块，每小块的质量分别为 $m_i$，离轴的距离 $r_{\bot i} = \sqrt{x_i^2 + y_i^2} $，角动量轴向分量为 $L_{iz}$ 则刚体的总角动量 $z$ 分量为

\begin{equation} L_z = \sum_i L_{iz} = \omega \sum_i m_i r_{ \bot i}^2~, \end{equation}

用定积分写成

\begin{equation} L_z = \omega \int r_ \bot ^2 \,\mathrm{d}{m} = \omega \int r_ \bot ^2\rho( \boldsymbol{\mathbf{r}} ) \,\mathrm{d}{V} ~. \end{equation}

　　定义刚体绕固定轴旋转的转动惯量（moment of inertia）为

\begin{equation} I = \int r_ \bot ^2 \,\mathrm{d}{m} = \int r_ \bot ^2\rho( \boldsymbol{\mathbf{r}} ) \,\mathrm{d}{V} ~. \end{equation}

注意角动量的大小不仅取决于刚体的质量分布，还取决于转轴的位置和方向。最后得刚体沿轴方向的角动量分量为

\begin{equation} L_z = I \omega ~, \end{equation}

可见 $L_z$ 和旋转角速度成正比。

3. 角加速度与力矩

预备知识 2　单摆

　　要分析刚体的转动与刚体所受外力的关系，就要对系统使用角动量定理。在这里 “系统” 指的就是刚体本身，不包含任何相对刚体运动的物体。我们要区分两种转轴：几何转轴是一条假想的有正方向的几何直线，刚体上任意一点都绕该直线做圆周运动，任何做定轴转动的刚体都存在几何转轴。物理转轴可以有粗细有质量、也可以对刚体提供约束力。物理转轴不是刚体做定轴转动所必须的，例如真空无重力环境中自由旋转的物体有几何转轴但不需要任何物理转轴。

　　约束物体做定轴转动的机械结构可能是多种多样的，例如通过轴承将物体套在一根固定的杆上，此时杆则不属于刚体的一部分，杆对旋转体的所有作用力都视为系统外力。另一种大同小异的情况例如杆固定在旋转体上一起转动，而杆两端套在固定的轴承上，此时杆可以视为刚体的一部分，故无需分析杆和物体之间的相互作用，轴承对杆的任何作用力都视为系统外力。又例如一个环形物体通过滑轮固定在一个环形轨道上转动，此时滚轮对物体的力为外力，几何转轴处没有任何其他结构。总之无论机械结构有多么复杂，我们只需要把机械结构中不发生形变的、作为整体绕几何轴旋转的部分看成刚体，外部对它的一切力（矩）都视为系统外力（矩），那么以下的分析就是成立的。

　　对系统使用 “角动量定理” 的式 1 ，注意等号两边是矢量，所以各个分量必须相等，我们有

\begin{equation} \tau_z = \frac{\mathrm{d}{L_z}}{\mathrm{d}{t}} ~, \end{equation}

将式 12 代入式 13 ，并利用角加速度的定义得

\begin{equation} \tau_z = I\alpha~. \end{equation}

这就是刚体定轴转动的动力学方程，其形式可类比质点做直线运动时的牛顿第二定律 $F = ma$：$\tau_z$ 可以类比力 $F$，$I$ 类比质量 $m$，$\alpha$ 类比加速度 $a$。

角动量轴向分量守恒

　　在定轴转动的情况下，根据式 13 ，当系统外对系统力矩的轴向分量 $\tau_z$ 为零时，角动量的轴向分量 $L_z$ 守恒。这意味着刚体的角加速度为零（式 14 ），也就是刚体做匀速转动或静止。类比到质点的直线运动就是当 $F = ma$ 中外力 $F = 0$ 时，加速度为零，质点做匀速运动，动量守恒。

　　可见和 “匀速运动不需要外力维持” 一样，匀速转动也并不需要转轴方向的外力矩维持。然而在日常生活中，正如水平直线轨道上具有初速度的滑块会由于与轨道的摩擦力，空气阻力等各种外力最终停止运动，具有初始角速度的物体也会在机械摩擦、空气阻力等外力矩的作用下最终停止转动，这与上述动量守恒并不矛盾。

例 1　物理摆

　　 物理摆（physical pendulum），也叫复摆（compound pendulum）。如图 2 ，已知质量为 $M$ 的刚体关于某转轴的转动惯量为 $I$，转轴到刚体质心的长度为 $r_c$，转轴和质心的连线与竖直方向夹角为 $\theta$，求刚体的运动方程。

图 2：物理摆

　　首先我们把刚体看做质点系，作质心到转轴的垂线，以垂足为坐标原点，以转轴指向纸内的方向为 $z$ 轴正方向，令质心的位置矢量为 $ \boldsymbol{\mathbf{r}} _c$（与转轴垂直），计算重力对刚体的合力矩为（例 1 ）

\begin{equation} \boldsymbol{\mathbf{\tau}} = M \boldsymbol{\mathbf{r}} _c \boldsymbol\times \boldsymbol{\mathbf{g}} ~. \end{equation}

由于 $ \boldsymbol{\mathbf{r}} _c$ 与转轴垂直，$ \boldsymbol{\mathbf{\tau}} $ 与转轴平行，所以

\begin{equation} \tau_z = Mg r_c \sin\theta~. \end{equation}

这说明，刚体所受力矩相当于质量为 $M$，长度为 $r_c$ 的单摆所受的力矩。代入式 14 得刚体摆的运动方程为

\begin{equation} I\ddot \theta = Mg r_c \sin\theta~, \end{equation}

可以验证当刚体的质量全部集中在质心时（$I = Mr_c^2$）我们就得到了单摆的运动方程式 4 。

　　若已知初始角度和角速度，由刚体定轴转动的动能定理可以求得任何角度时的角速度，详见例 1 。

例 2　箱子倾倒

　　如图 3 ，一长方体箱子初始时倾角为 $\theta_0$，以初速度 0 无滑动倾倒，求其运动方程。

图 3：箱子倾倒

　　这和例 1 属于同一模型，公式不再赘述。事实上，长方体箱子的旋转运动和其截面长方形的旋转一致，这本质上是一个二维问题。初始时若箱子的质心在转轴右边时，箱子必然顺时针倾倒，反之逆时针倾倒。若初始时质心恰好在转轴上方，那么这是一个不稳定平衡，任何微小的扰动都会使箱子向某一侧倾倒。

例 3　

未完成：未完成。链接到这里。

图 4：请添加图片描述

4. 垂直轴的角动量

　　以上的讨论中，我们有意避免讨论垂直轴方向的角动量分量 $L_x, L_y$。一般情况下，我们不能保证他们是守恒的。在一些特殊情况下，例如刚体的形状和质量分布关于转轴呈某种轴对称，那么容易证明刚体（关于任意固定点）的总角动量 $ \boldsymbol{\mathbf{L}} $ 只可能延转轴方向，即 $L_x = L_y = 0$ 守恒。

　　在一些不对称的情况下，例如一个倾斜的细杆绕转轴旋转，转轴就需要对细杆施加一个不停旋转的力矩，细杆也会对轴施加一个反力矩，这类似于作用力和反作用力，详见 “刚体定轴转动 2”。

1. ^ 例如圆盘、长方形、正三角形等绕对称轴旋转