贡献者: addis
1本文使用原子单位制。库仑波函数(Coulomb wave function)是类氢原子的散射态波函数。是库仑势能 $V(r) = -Z/r$($Z > 0$)下定态薛定谔方程对能量 $E > 0$ 的解。
库仑波函数常用的边界条件有两种,以波数 $ \boldsymbol{\mathbf{k}} $ 的平面波入射(球面波出射)的库仑波函数记为 $\psi_{ \boldsymbol{\mathbf{k}} }^{(+)}( \boldsymbol{\mathbf{r}} )$,平面波出射(球面波入射)的散射态记为 $\psi_{ \boldsymbol{\mathbf{k}} }^{(-)}( \boldsymbol{\mathbf{r}} )$。第一种边界条用于计算散射2
\begin{equation}
\psi_{ \boldsymbol{\mathbf{k}} }^{(\pm)}( \boldsymbol{\mathbf{r}} ) \overset{kr \mp \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} \to +\infty}{\longrightarrow} \frac{1}{(2\pi)^{3/2}} \left\{ \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} \pm \mathrm{i} \eta \ln\left(kr \mp \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} \right) }
+ f^{(\pm)}( \hat{\boldsymbol{\mathbf{k}}} ) \frac{ \exp\left[\pm \mathrm{i} kr \mp \mathrm{i} \eta \ln\left(2kr\right) \right] }{r} \right\} ~.
\end{equation}
在抛物线坐标系中可以解得3满足该边界的库仑波函数的解析式为4(Matlab 和 Mathematica 代码)
\begin{equation}
\psi_{ \boldsymbol{\mathbf{k}} }^{(\pm)}( \boldsymbol{\mathbf{r}} ) = \frac{1}{(2\pi)^{3/2}} \Gamma(1\pm \mathrm{i} \eta) \mathrm{e} ^{-\pi\eta/2} \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} } {_1F_1}(\mp \mathrm{i} \eta; 1; \pm \mathrm{i} kr - \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} )~.
\end{equation}
其中 $\eta = -mZ/k$ 叫做
Sommerfeld 参数,$k$ 是能量为 $E = k^2/(2m)$ 的
平面波的波数,$Z$ 是原子核的质子数($Z > 0$)。上式满足
\begin{equation}
\psi_{ \boldsymbol{\mathbf{k}} }^{(+)}( \boldsymbol{\mathbf{r}} ) = \psi_{- \boldsymbol{\mathbf{k}} }^{(-)}( \boldsymbol{\mathbf{r}} )^*~,
\end{equation}
\begin{equation}
\langle{\psi_{ \boldsymbol{\mathbf{k}} }^{(\pm)}}|{\psi_{ \boldsymbol{\mathbf{k}} '}^{(\pm)}}\rangle = \delta( \boldsymbol{\mathbf{k}} - \boldsymbol{\mathbf{k}} ')~.
\end{equation}
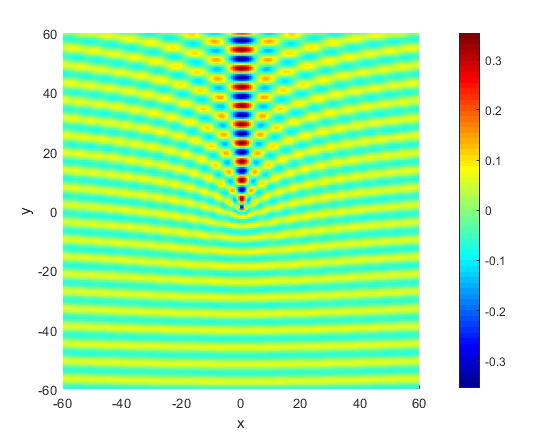
图 1:$\psi_{ \boldsymbol{\mathbf{k}} }^{(+)}( \boldsymbol{\mathbf{r}} )$ 或 $\psi_{- \boldsymbol{\mathbf{k}} }^{(-)}( \boldsymbol{\mathbf{r}} )$ 的实部,$Z = 5$, $ \boldsymbol{\mathbf{k}} = \hat{\boldsymbol{\mathbf{y}}} $,$\eta = -5$。当 $y \to -\infty$ 时趋近于平面波。从经典力学考虑,粒子越靠近原子核入射偏折越多。注意左右两边的平面波偏折后会相交并产生干涉。
另一种边界条件是在球坐标中用分离变量解薛定谔方程,本征态为(我们称为库仑球面波)
\begin{equation}
\psi_{l,m,k}( \boldsymbol{\mathbf{r}} ) = \frac{1}{r} \sqrt{\frac{2}{\pi}} F_l(\eta, kr) Y_{l,m}( \hat{\boldsymbol{\mathbf{r}}} )~,
\end{equation}
满足正交归一条件
\begin{equation}
\left\langle \psi_{l',m',k'} \middle| \psi_{l,m,k} \right\rangle = \delta_{l,l'}\delta_{m,m'} \delta(k'-k)~.
\end{equation}
1. 球坐标中的库仑波函数
球坐标中的库仑波函数与上面 “库仑平面波” 之间的关系,可以类比平面波与球面波的关系。即 $k$ 相同的所有方向的平面波基底张成的空间与球面波基底张成的空间相同,即能量为 $E = k^2/(2m)$ 的无穷维子空间。
库仑势的薛定谔径向方程(式 3 )为
\begin{equation}
-\frac{1}{2m} \frac{\mathrm{d}^{2}{u}}{\mathrm{d}{r}^{2}} + \left[-\frac{Z}{r} + \frac{l(l+1)}{2mr^2} \right] u = \frac{k^2}{2m}u~.
\end{equation}
其中 $u(r)$ 是约化径向波函数,$l$ 是角量子数,$Z > 0$ 是原子核的质子数。方括号中的等效势能如
图 2 。
图 2:球坐标中的径向等效势能
使用 $\eta = -mZ/k$ 以及 $\rho = kr$ 换元,得
\begin{equation}
\frac{\mathrm{d}^{2}{u}}{\mathrm{d}{\rho}^{2}} + \left[1 - \frac{2\eta}{\rho} - \frac{l(l+1)}{\rho^2} \right] u = 0~,
\end{equation}
两个线性无关解为
第一类库仑函数 $F_l(\eta, \rho)$ 和
第二类库仑函数 $G_l(\eta, \rho)$
。散射态中,我们假设 $k > 0$($E > 0$)。但理论上我们也可以取 $k$ 为正虚数($E < 0$),这样当 $E$ 为束缚态能量时就可以得到束缚态的径向波函数(
式 6 )。
可以证明完备正交归一的库仑球面波为
\begin{equation}
\left\lvert C_{l,m}(k) \right\rangle = \frac{1}{r} \sqrt{\frac{2}{\pi}} F_l(\eta, kr) Y_{l,m}( \hat{\boldsymbol{\mathbf{r}}} )~,
\end{equation}
满足(参考 “
球谐展开中径向函数的归一化”)
\begin{equation}
\left\langle C_{l',m'}(k') \middle| C_{l,m}(k) \right\rangle = \delta_{l,l'}\delta_{m,m'}\delta(k-k')~.
\end{equation}
现在可以将第一种边界条件的库仑波函数(式 1 )展开为
\begin{equation}
\psi_{ \boldsymbol{\mathbf{k}} }^{(\pm)}( \boldsymbol{\mathbf{r}} ) = \sum_{l,m} a_{l,m}^{(\pm)}( \boldsymbol{\mathbf{k}} ) \left\lvert C_{l,m}(k) \right\rangle ~,
\end{equation}
其中
\begin{equation}
a_{l,m}^{(\pm)}( \boldsymbol{\mathbf{k}} ) = \frac{ \mathrm{i} ^l}{k} \mathrm{e} ^{\pm \mathrm{i} \sigma_l} Y_{l,m}^* ( \hat{\boldsymbol{\mathbf{k}}} )~,
\end{equation}
$\sigma_l(\eta)$ 是库仑相移(
式 9 )。注意 $a_{l,m}$ 并不是 $ \langle{C_{l,m}(k)}|{\psi_{ \boldsymbol{\mathbf{k}} }^{(\pm)}}\rangle $,后者模长为无穷大,也可记为 $a_{l,m}\delta(0)$。
2. 投影到库仑平面波
与平面波的情况(傅里叶变换)类似,要将一个球谐展开的波函数 $ \left\lvert f \right\rangle $ 投影到库仑波函数上,就先投影到库仑球面波上,然后进行幺正变换
\begin{equation}
\langle{\psi_{ \boldsymbol{\mathbf{k}} }^{(\pm)}}|{f}\rangle = \sum_{l,m} a_{l,m}^{(\pm)}( \boldsymbol{\mathbf{k}} )^* \left\langle C_{l,m}(k) \middle| f \right\rangle ~.
\end{equation}
若 $ \left\lvert f \right\rangle $ 的 scaled 径向波函数为 $u_{l,m}(r)$,也就是说
\begin{equation}
\left\lvert f \right\rangle = \frac{1}{r}\sum_{l,m}u_{l,m}(r) Y_{l,m}( \hat{\boldsymbol{\mathbf{r}}} )~.
\end{equation}
代入
式 13 有
\begin{equation}
\langle{\psi_{ \boldsymbol{\mathbf{k}} }^{(\pm)}}|{f}\rangle = \frac{1}{k} \sum_{l,m} g_{l,m}^{(\pm)}(k) Y_{l,m}( \hat{\boldsymbol{\mathbf{k}}} )~,
\end{equation}
其中
\begin{equation}
g_{l,m}^{(\pm)}(k) = \sqrt{\frac{2}{\pi}} \mathrm{i} ^{-l} \mathrm{e} ^{\mp \mathrm{i} \sigma_l} \int_0^\infty F_l(\eta, kr) u_{l,m}(r) \,\mathrm{d}{r} ~.
\end{equation}
将波函数做傅里叶变换和投影到库仑波函数有什么区别呢?例如做氢原子电离的 TDSE,若想求 $t = +\infty$ 时的动量分布,理论上只要在 $t$ 足够大时做傅里叶变换即可,但如果 $t$ 不够大(电场已消失),电离波包所受的库仑力还不可忽略,那么虽然得到了瞬时的动量分布,但却与 $t = +\infty$ 的不同。这时因为动量算符与哈密顿算符不对易,动量不守恒。但若在电场消失的时候,投影到 $\psi_{ \boldsymbol{\mathbf{k}} }^{(-)}$ 上,由于它是哈密顿的本征函数,投影的模方(概率)不会随时间改变。
1. ^ 参考资料: [1],Wikipedia,据说 [2] 也有。另一个是 “F Morales et al 2016 J. Phys. B: At. Mol. Opt. Phys. 49 245001” 的附录。
2. ^ 参考 [1] 式 12.211
3. ^ 推导见 [1]。
4. ^ Bransden [1] 12.222, 12.223
[1] ^ Bransden, Physics of Atoms and Molecules, 2ed
[2] ^ Eugen Merzbacher. Quantum Mechanics 3ed