贡献者: addis
图 1:一维(平面)简谐波
图 2:二维平面简谐波
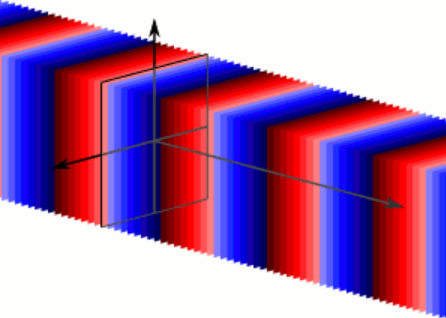
图 3:三维平面简谐波(来自 Wikipedia)
1通常我们说 “波” 时,它几乎可以是任意形状和任何空间维度的,例如一个波包,或者从一点向各个方向传播的球面波。但我们这里讨论一种最简单的波动,即延单一方向传播的简谐波,也叫做简谐平面波(sinusoidal plane wave)。“简谐” 的意思是,在任意时刻,它在传播方向的波形是一个简谐函数,即正弦或余弦函数平移一个相位,且长度是无穷大。由于现实中不存在无限长的波,所以和 “质点” 一样,平面波属于一个理想化的模型。简谐平面波既可以是横波也可以是纵波(子节 2 )。
“平面” 这个词的由来是因为三维空间中该波的等相位面(见下文)都是平面,但广义来说平面波所在的空间可以是任意维度的,例如二维薄膜上的类似波动(图 2 )虽然等相位的是直线,但不叫 “直线波” 而仍叫 “平面波”,一维波动例如琴弦的波动也同理(图 1 )。当然,在一维情况下直接叫简谐波较合适,因为没有 “等相位线/面” 的概念。
在任何维度中,简谐平面波都往往被简称为简谐波或者平面波,后者频繁在量子力学中使用,小时百科的量子力学部分也会大量使用平面波这个简称,无论波动是几维的。本文使用前者。严格来说,平面波未必是简谐的,只需要等相位面都是平面即可:例如振幅和波长随空间变化,频率随时间变化也仍然可能是平面波。而简谐波也未必是平面的,球面波在每个传播的方向也可以简谐函数。用词的具体含义读者可以容易地通过上下文判断出来。
1. 一维简谐波
我们先来看一个一维的简谐波,一个常用的例子是一根无限长的弦,静止的时候弦与 $x$ 轴重合,在任何时刻 $t$,弦的波函数(即形状)可以用 $y(x, t)$ 来描述。若
\begin{equation}
y(x, t) = A \cos\left(k x - \omega t + \phi_0\right) ~.
\end{equation}
则我们把这个波函数称为
一维简谐波,如
图 1 所示
2。
3
我们定义图中的 $A$ 为振幅,定义一个空间周期为波长(wave length),记为 $\lambda$。与波长一一对应的一个量是式 1 中的 $k$,称为波数(wave number)。波长与波数的关系可以类比简谐振子的角频率 $\omega$ 与时间周期 $T$ 的关系(式 13 ),即
\begin{equation}
k = \frac{2\pi}{\lambda}~.
\end{equation}
式中 $\cos$ 函数的参数 $\phi = (k x - \omega t + \phi_0)$ 叫做
相位(phase),相位取决于位置和时间。令 $x=0$,$t=0$,相位为 $\phi_0$,是一个常数,叫做
初相位。即使对同一个简谐波,初相位也和坐标系的选取有关:例如把坐标系平移后,令新坐标为 $x' = x - \Delta x$,那么新坐标系中的初相位就是 $\phi'_0 = \phi_0 + k\Delta x$。由 $\cos$ 的周期性,理论上可以给初相位 $\phi_0$ 加减 $2\pi$ 的任意整数倍而不影响波的形状。
我们再来看波函数随时间的变化,如果在弦的某个位置做一个标记并观察其运动,则式 1 中 $x$ 可视为常数,我们立即得到一个简谐振动 $A \cos\left(\omega t + \varphi_0\right) $,角频率为 $\omega$,初相位为4 $\varphi_0 = -kx - \phi_0$。
我们在观察简谐波的时候,通常会想象它在移动(虽然弦上每个点的 $x$ 坐标并不改变),我们把这种视觉上的移动的速度叫做波速(wave velocity) $v$,更准确来说叫做相速度(phase velocity)(以后还会定义群速度)。把式 1 稍作整理得
\begin{equation}
y(x, t) = A\cos \left[k \left(x - \frac{\omega}{k} t \right) + \phi_0 \right] ~.
\end{equation}
由于函数 $f(x - x_0)$ 可以看做 $f(x)$ 向 $x$ 轴正方向
平移 $x_0$ 得到的函数,上式也可以看做 $t = 0$ 时刻的波函数向 $x$ 轴正方向平移 $\omega t/k$ 得到的波函数。将平移距离除以 $t$ 就得到了单位时间移动的距离,即波速
\begin{equation}
v = \frac{\omega}{k}~.
\end{equation}
如果将 $\omega = 2\pi/T$ 和 $k = 2\pi/\lambda$ 代入上式,得到波速的另一个表达式
\begin{equation}
v = \frac{\lambda}{T}~,
\end{equation}
这里的 $T$ 是振动周期。也可以令振动频率 $f = 1/T$,则上式又变为
\begin{equation}
v = \lambda f~.
\end{equation}
2. 横波与纵波
以上我们看到的波函数的值既可以表示于传播方向垂直方向的振动幅度,也可以表示延传播方向的振动幅度。当振动的方向与波的传播方向垂直时(如琴弦的波动),我们把这种波叫做横波(transverse wave);若振动方向和传播方向垂直(例如一个长弹簧通过伸缩产生的波)则称为纵波(longitudinal wave)。纵波的波函数与横波相同,只是函数值的意义由垂直方向的位移改为了平行方向的位移(不妨记为 $\xi$)
\begin{equation}
\xi = A \cos\left(k x - \omega t + \phi_0\right) ~.
\end{equation}
广义来说,振幅可以是一个任意方向的矢量 $ \boldsymbol{\mathbf{A}} $,它可以既不平行也不垂直于传播方向,此时它可以认为是横波和纵波的叠加。
3. 二维和三维的平面简谐波
如图 2 ,我们可以用函数 $z(x,y,t)$ 表示一个二维的简谐波(横波)。波长的定义与一维情况相同,在 $k = 2\pi/\lambda$ 的基础上我们还需要一个传播方向,我们定义波矢 $ \boldsymbol{\mathbf{k}} $ 的方向为波速的方向。
观察图中的波可以发现,沿波矢方向移动 $l$,相位变化为 $kl$,沿垂直波矢方向移动 $l$,相位不改变,沿任意其他方向移动 $l$,相位变化为 $kl\cos\theta$,其中 $\theta$ 是移动方向与 $ \boldsymbol{\mathbf{k}} $ 方向的夹角。垂直于波矢的任意直线就是二维简谐波的等相位面(线)。我们可以用矢量的点乘来表示相位随空间的变化
\begin{equation}
\Delta\phi = \boldsymbol{\mathbf{k}} \boldsymbol\cdot \Delta \boldsymbol{\mathbf{r}} = k_x \Delta x + k_y \Delta y~.
\end{equation}
于是我们可以写出波函数为
\begin{equation}
z = A \cos\left( \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} - \omega t + \phi_0\right) ~.
\end{equation}
要表示纵波,同样把 $z$ 换位 $\xi$ 即可。
类似地,三维空间中的简谐波可表示为
\begin{equation}
\boldsymbol{\mathbf{s}} = \boldsymbol{\mathbf{A}} \cos\left( \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} - \omega t + \phi_0\right) ~,
\end{equation}
其中 $ \boldsymbol{\mathbf{k}} $ 和 $ \boldsymbol{\mathbf{r}} $ 是三维矢量。注意这里的 $ \boldsymbol{\mathbf{r}} $ 表示介质静止时某质点的位矢。如果波函数表示横波,矢量振幅 $ \boldsymbol{\mathbf{A}} $ 必须垂直于波矢 $ \boldsymbol{\mathbf{k}} $,其方向叫做
极化方向。如果波函数表示纵波,$ \boldsymbol{\mathbf{A}} $ 必须与 $ \boldsymbol{\mathbf{k}} $ 同向。
光是横波,光的偏振方向就是指 $ \boldsymbol{\mathbf{A}} $ 的方向,所以光有两个相互垂直的偏振方向。
4. 复数形式
用复数表示波函数,往往可以化简书写和计算。类比式 3 ,我们可以把简谐波表示为指数形式5
\begin{equation}
\tilde { \boldsymbol{\mathbf{s}} } = \boldsymbol{\mathbf{A}} \exp\left[ \mathrm{i} ( \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} - \omega t + \phi_0)\right] ~.
\end{equation}
注意在经典物理(非量子力学)中,该函数只有实部表示质点的位移,虚部无物理意义。通常也可以把初相位合并到振幅中,令
复振幅为
\begin{equation}
\tilde { \boldsymbol{\mathbf{A}} } = \boldsymbol{\mathbf{A}} \mathrm{e} ^{ \mathrm{i} \phi_0}~,
\end{equation}
则上式记为
\begin{equation}
\tilde { \boldsymbol{\mathbf{s}} } = \tilde { \boldsymbol{\mathbf{A}} } \exp\left[ \mathrm{i} ( \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} - \omega t)\right] ~.
\end{equation}
1. ^ 参考 Wikipedia 相关页面 1以及相关页面 2。
2. ^ 需要注意的是,图中的横轴是位置 $x$ 而不是时间 $t$,要避免将质点振动的位移—时间图与该图混淆。
3. ^ 根据 $\cos$ 函数的性质,也可以把波函数记为 $y(x, t) = A \cos\left(\omega t - k x + \phi_0\right) $,或者用 $\sin$ 函数表示。但我们选择正文中的规范。
4. ^ 由于余弦函数是偶函数,我们不妨将 $\cos$ 的参数取相反数使 $\omega t$ 的符号为正。
5. ^ 现在我们知道为什么振动的指数形式中 $\omega t$ 要带一个负号了,这样就可以让波动的指数形式中 $ \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} $ 项为正。