压强体积图

贡献者： addis; _Eden_; FFjet

本文处于草稿阶段。

预备知识　状态量和过程量

　　根据理想气体状态方程，我们可以得知给定量的理想气体的宏观状态只有两个自由度。在例 1 中我们说到可以在压强 $P$，体积 $V$，温度 $T$ 等宏观量中任取两个来作为该系统的状态量，完全确定系统的宏观状态。而最常见的作法是取压强和体积 $P,V$。于是自然地，我们可以用一个二维直角坐标系 $P$-$V$ 中的一点来描绘理想气体某时刻的状态及其变化，称为压强体积图。该平面就是理想气体的（宏观）状态空间。注意在讨论 $P$-$V$ 上的状态变化时，我们往往假设气体始终处于准平衡的状态。

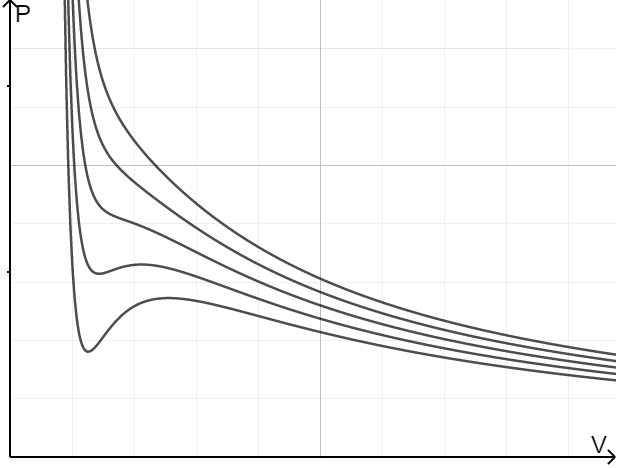
　　对于其他的气体模型（如范德瓦尔斯气体），虽然状态方程与理想气体不同，但以上讨论仍然成立，所以同样可以用 $P$-$V$ 图描述其状态的变化。

未完成：还可以举几个等体线、等压线、绝热线的图片作为例子

1. 等温线

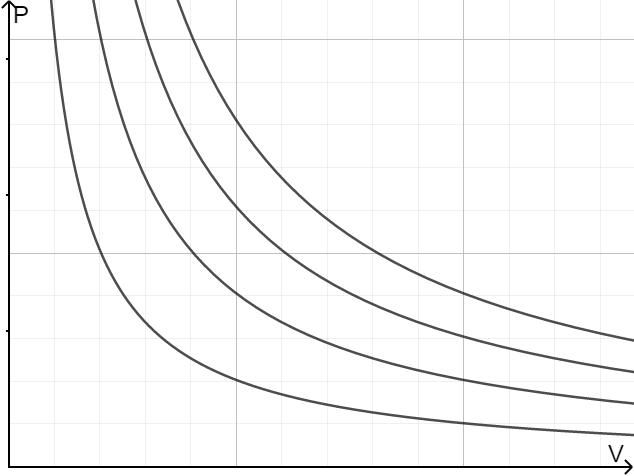
　　为了直观地表现它们的关系，我们可以借助压强体积图，在上面画出一条曲线——曲线上每个点表示在当前温度下不同压强所对应的不同体积。

图 1：理想气体的等温线

图 2：范德瓦尔斯气体的等温线

　　等温线帮助我们分析压强、体积与温度的关系。例如图 1 中等温线是反比例函数，意味着理想气体在同一温度下压强与体积成反比。

2. 压强体积图与做功

体积、压强与做功

　　现有一个体积 $V$ 可变的容器，在容器壁上可以安装探测器来测量内部气体的压强 $P$。只要气体处于平衡态，气体的压强就处处相等。现在我们考虑这样一个问题——改变容器的体积，需要对容器做多少功（或者容器对外界做多少功）？

　　假设容器是长方体，横截面是 $S$，那么这块面上受气体压强的力为 $P\cdot S$。如果改变长方体的体积，使它长度增加 $\Delta x$（假设在这个过程中压强变化不大），那么气体对外做功为 $F\cdot \Delta x=P\cdot S\Delta x=P\Delta V$。于是我们得出结论 $\Delta W=P\Delta V$，这不仅对长方体容器成立，对任意形状的容器都成立。

压强体积图上任意曲线的做功

　　由于容器在改变体积的过程中，气体的压强可以发生变化，在一个复杂过程中做功不能用简单的 $P\Delta V$ 概括，但我们却可以划分为无穷多个小过程，每一个小过程中压强变化不大，做功近似地可以看成是 $P\Delta V$。这样一来，总的做功就是 $P \,\mathrm{d}{V} $ 的积分了。

　　图像可以帮助我们方便地分析这个问题。对于 $P-V$ 图中的一条曲线，设容器从点 $1$ 沿着曲线变化到点 $2$——曲线上每一个点表明了气体在当时的体积和压强。

图 3：$P$-$V$ 图中气体做的功

　　如图 3 所示，做功

\begin{equation} W = \int_{V_1}^{V_2}P(V) \,\mathrm{d}{V} ~. \end{equation}

　　由积分关系式可得，做功就是 $P$-$V$ 曲线下方的面积，也就是图中标注的阴影部分的面积。

图 4：$P-V$ 图中闭合路径气体做的功

　　如图 4 所示，如果是一个闭合路径，在气体状态沿着它走的过程中，对外做功就是闭合路径围出的面积（顺时针为正）。

例 1　理想气体在等温压缩需要做的功

　　一个装有理想气体的体积可变的导热容器，放在温度为 $T$ 的恒温箱中，保证其温度恒为 $T$。现在缓慢地将它从体积 $V_0$ 压缩成 $V_1$，求这个过程中需要对容器壁做的功为多大。

　　解：气体对外界做功 $P\Delta V$，则外界对气体做功为 $-P\Delta V$。由理想气体状态方程式 1 可得 $P=\frac{nRT}{V}$。所以

\begin{equation} \begin{aligned} \int_{V_0}^{V_1} -P \,\mathrm{d}{V} &=\int_{V_0}^{V_1} -\frac{nRT}{V} \,\mathrm{d}{V} \\ &=nRT \ln \left(\frac{V_0}{V_1} \right) ~. \end{aligned} \end{equation}