贡献者： addis
- 本文需要更多讲解，便于帮助理解。
- 本文存在未完成的内容。
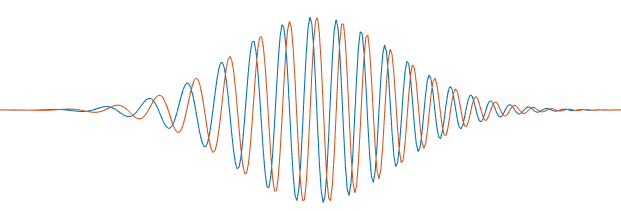
我们这里要讨论的是量子力学中单个粒子的一个特定的一维波函数 $\psi(x,t)$。它描述的粒子的位置分布是一个高斯分布（正态分布）。
未完成：详细讨论啁啾，另外注意随着波函数演化，位置和动量分部不再满足最小不确定性原理。
设 $t = 0$ 时的波函数（已归一化）
\begin{equation}
\psi (x,0) = \frac{1}{(2\pi\sigma_x ^2)^{1/4}} \mathrm{e} ^{-(x - x_0)^2/(2\sigma_x)^2} \mathrm{e} ^{ \mathrm{i} \frac{p_0}{\hbar}x}~.
\end{equation}
那么动量表象波函数具有对称的形式
1
\begin{equation} \psi (p,0) = \frac{1}{(2\pi\sigma_p^2)^{1/4}} \mathrm{e} ^{-(p - p_0)^2/(2\sigma_p)^2} \mathrm{e} ^{- \mathrm{i} \frac{x_0}{\hbar }(p - p_0)}~,
\end{equation}
其中 $\sigma_x$ 为位置的标准差，$\sigma_p$ 为动量的标准差，满足不确定原理
\begin{equation} \sigma_x\sigma_p = \frac{\hbar}{2}~.
\end{equation}
含时波函数为
\begin{equation}\begin{aligned} \psi (x,t) = &\frac{1}{(2\pi\sigma_x^2)^{1/4} \sqrt{1 + { \mathrm{i} \hbar t}/(2m \sigma_x^2)}}
\exp \left[\frac{-(x - x_0 - p_0 t/m)^2}{(2\sigma_x )^2 \left(1 + \frac{ \mathrm{i} \hbar t}{2m \sigma_x^2} \right) } \right] \exp \left[\frac{ \mathrm{i} p_0}{\hbar } \left(x - \frac{p_0 t}{2m} \right) \right] ~.
\end{aligned}\end{equation}
一般来说，波包扩散是因为初始时存在一定的速度分布。从经典力学来看，波包的长度应该与时间成正比，但下面会看到波包长度与 $\sqrt{t}$ 成正比。
记扩散后的高斯波包的标准差为 $\bar\sigma_x(t)$，则稍加推导有
\begin{equation}
\bar\sigma^4_x(t) = \sigma_x^4 + \left(\frac{\hbar t}{2m} \right) ^2~.
\end{equation}
当 $t$ 很大时，近似有
\begin{equation}
\bar\sigma_x(t) = \sqrt{\frac{\hbar t}{2m}}~.
\end{equation}
（与 $\sigma_x$ 无关！）这就是为什么质量小的物体更容易显示出波动性。对于电子有 $\bar\sigma_x(t) \sim 0.0076\sqrt{t}$（国际单位），在厘米量级。
让波包随时间变长的原因和产生啁啾的原因都是下面推导中的动能因子 $ \exp\left(- \mathrm{i} k^2 t\right) $。它使得高斯波包在 $t > 0$ 时不再是 transform limited 的，也就是不再恰好满足 $\sigma_x \sigma_p = \hbar/2$。
1. 推导
初状态
以下为书写方便使用原子单位制。如果我们想要一维波函数的概率分布为高斯分布，即
\begin{equation}
\left\lvert \psi (x) \right\rvert ^2 = \frac{1}{\sigma_x \sqrt{2\pi}} \exp\left[-\frac{x^2}{2\sigma_x^2}\right] ~.
\end{equation}
先假设波函数为实数，有
\begin{equation}
\psi (x) = \frac{1}{(2\pi\sigma_x^2)^{1/4}} \exp\left[-\frac{x^2}{(2\sigma_x)^2}\right] ~.
\end{equation}
变换到动量表象，即做反傅里叶变换，借助高斯积分
式 7 得
\begin{equation}
\psi(p) = \frac{1}{(2\pi\sigma_p^2)^{1/4}} \exp\left[-\frac{p^2}{(2\sigma_p)^2}\right] ~.
\end{equation}
其中 $\sigma_p = 1/(2\sigma_x)$，可见高斯波包一个独特的性质就是在位置和动量表象下都是高斯分布。
由于波函数为实数，动量平均值为零（定理 1 ）。为了让波函数有一个动量 $p_0$，而维持 $ \left\lvert \psi(x) \right\rvert ^2$ 和 $ \left\lvert \psi(p) \right\rvert ^2$ 的形状不变，我们可以直接将动量表象中的波函数平移 $p_0$，得
\begin{equation}
\psi (p) = \frac{1}{(2\pi\sigma_p^2)^{1/4}} \exp\left[-\frac{(p - p_0)^2}{(2\sigma_p)^2}\right] ~.
\end{equation}
由傅里叶变换的性质（
式 14 ），对应的位置表象波函数需要乘以因子 $ \exp\left( \mathrm{i} p_0 x\right) $ 变为
\begin{equation}
\psi(x) = \frac{1}{(2\pi\sigma_x^2)^{1/4}} \exp\left[-\frac{x^2}{(2\sigma_x)^2}\right] { \mathrm{e} ^{ \mathrm{i} {p_0}x}}~.
\end{equation}
类似地，也可以再将 $\psi(x)$ 平移 $x_0$
\begin{equation}
\psi (x) = \frac{1}{(2\pi\sigma_x^2)^{1/4}} \exp\left[-\frac{(x-x_0)^2}{(2\sigma_x)^2}\right] \mathrm{e} ^{ \mathrm{i} p_0 (x-x_0)}~.
\end{equation}
而 $\psi(p)$ 则需要乘以因子 $ \exp\left(- \mathrm{i} x_0 p\right) $
\begin{equation}
\psi(p) = \frac{1}{(2\pi\sigma_p^2)^{1/4}} \exp\left[-\frac{(p - p_0)^2}{(2\sigma_p)^2}\right] \mathrm{e} ^{- \mathrm{i} x_0 p}~.
\end{equation}
将以上两式同乘一个常数 ${ \mathrm{e} ^{ \mathrm{i} {p_0}{x_0}}}$ 就得到
式 1 和
式 2 。
时间演化的推导
按照式 5 ，把式 2 乘以时间因子 $ \exp\left(- \mathrm{i} \frac{p^2}{2m}t\right) $，再做反傅里叶变换，并把积分写为
\begin{equation}
\psi(x, t) = C\int_{-\infty}^{+\infty} \exp\left[-a^2(p-p_0)^2 + b(p-p_0) + c\right] \,\mathrm{d}{p} ~.
\end{equation}
的形式，得
\begin{equation}
a = \sigma_x^2 + \frac{ \mathrm{i} t}{2m}~, \qquad
b = \mathrm{i} (x-x_0) - \frac{ \mathrm{i} pt}{m}~, \qquad
c = \mathrm{i} p_0 \left(x - \frac{p_0}{2m} t \right) ~.
\end{equation}
由高斯积分
式 7 得积分结果为
\begin{equation}
\psi(x, t) = C\sqrt{\frac{\pi}{a}} \exp\left(\frac{b^2}{4a}\right) \mathrm{e} ^c~.
\end{equation}
整理后得
式 4 。
1. ^ 也可以把式 1 和式 2 同时除以常数 $ \mathrm{e} ^{ \mathrm{i} p_0 x_0}$ 使式 1 最后的 $x$ 变为 $x-x_0$，式 2 最后的 $p-p_0$ 变为 $p$。
致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者
热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。
