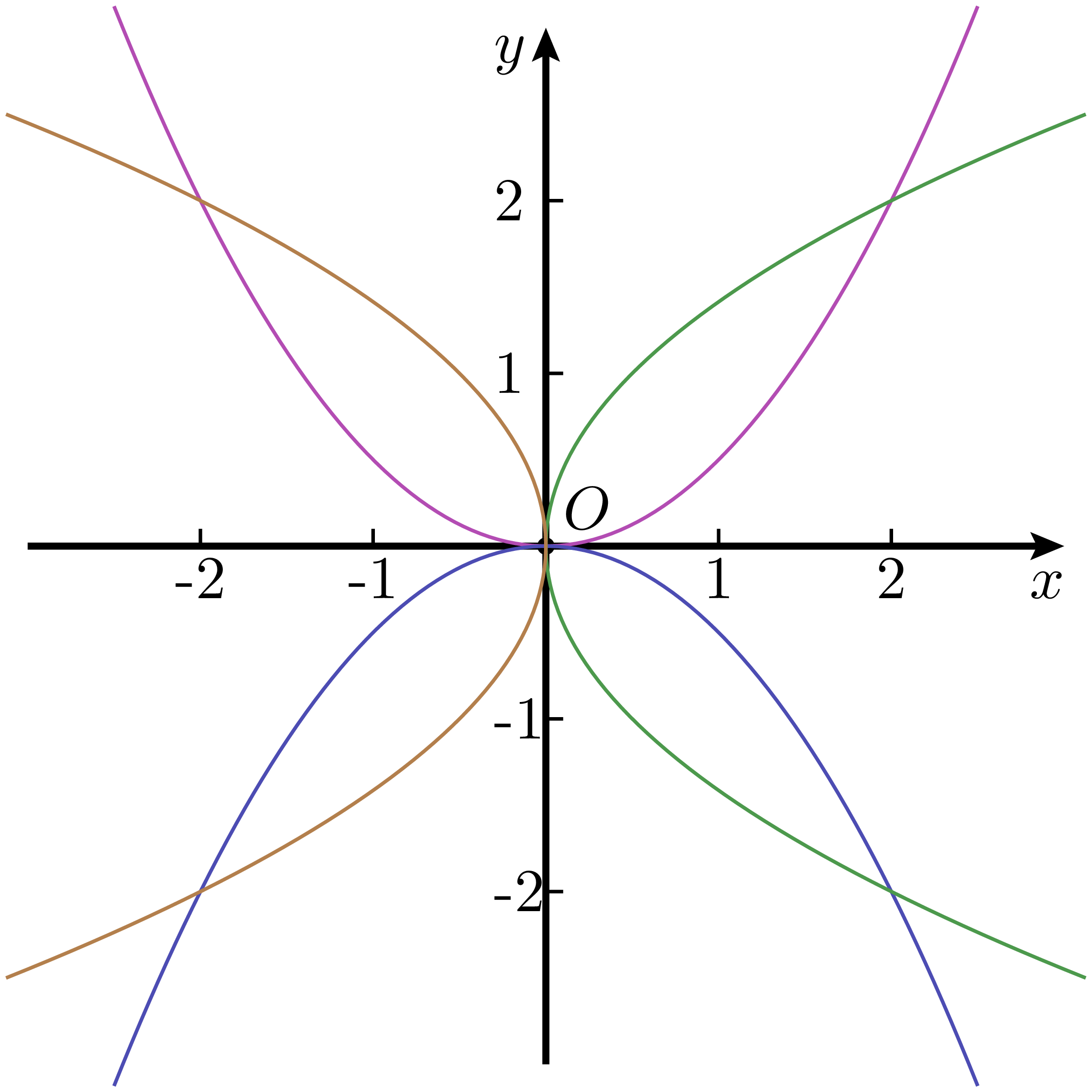抛物线（高中）

                     

贡献者： 欄、停敘; addis; ACertainUser

预备知识　解析几何，圆，双曲线，点到直线的距离

　　 不知道读者在初次接触双曲线时，是否产生了一种似曾相识的感觉：它的一支看起来与初中阶段学习过的二次函数图像——“抛物线” 非常相似：两者都不封闭，都有一个开口，形状略微弯曲，并向无限延伸，甚至同样具有对称轴。相信一些读者可能早已不禁在心中将双曲线的一支看成抛物线，认为双曲线不过是 “两个抛物线” 的组合而已。

　　 这种误解并不罕见。抛物线和双曲线在图像上确实有相似之处，但它们在几何定义、解析式结构以及性质等方面有着明显的差别。之所以容易混淆，很大程度上与初中学习的重点有关。那时更注重的是二次函数的代数表达与图像之间的关系，例如开口方向、对称轴、顶点坐标和零点等。这些内容有助于建立对抛物线的基本印象，但主要停留在函数视角，对抛物线作为几何图形本身的理解较为有限。

　　 大多数人对抛物线的印象，往往停留在现实生活中物体被抛出后所形成的轨迹。在理想状态下，这类轨迹正是一条抛物线，这也正是 “抛物线” 名称的来源。然而，随着人们的进一步研究发现，抛物线并不仅仅出现在物理运动中，它还具有独特的几何性质，在许多实际工程中发挥着重要作用。例如，雷达天线的反射面通常设计成抛物面结构，原因就在于抛物线具备一种精确的聚焦特性：来自远处的平行电磁波在抛物面上反射后，会准确地汇聚到焦点；而从焦点出发的信号，也能被反射成方向一致的平行波。这一聚焦能力，使抛物面非常适合实现能量的集中与传输，使抛物线广泛出现于雷达、卫星通信设备、汽车大灯以及太阳能灶等场景中。

1. 抛物线的定义

　　 由于初中阶段已经花了很多力气研究二次函数，并且基本了解了抛物线的图像特征，因此此处不再从函数的角度展开，而是直接进入定义的探讨。

　　 在研究椭圆和双曲线的过程中，曾尝试将圆的定义加以推广。圆可以看作是满足条件 $|O_1P| = |O_2P| = r$ 的点 $P$ 的集合，其中 $O_1$ 与 $O_2$ 是重合的点，二者之间的距离 $d(O_1,O_2)=0$。如果放宽这个限制，即允许 $d(O_1,O_2)$ 不为零，并且打开第一个等号，就可以得到椭圆和双曲线这两种新曲线，这在之前已经探究过了。那么，如果不打开第一个等号，而是改为将第二个等号 “打开”，只要求 $|O_1P| = |O_2P|$ 呢？之前提到过，在这种设定下，点 $P$ 的轨迹就是所有到两个定点距离相等的点——也就是这两点连线的垂直平分线。看起来，这样的修改似乎已经没有什么进一步变化的空间了。1不过，不妨换个思路。既然要求的是两个距离相等，而之前学过的 “距离” 可以是两点之间的距离、两条平行线之间的距离，或者点到直线的距离，那有没有可能试着改变一下条件中的几何元素呢？

　　 比如，如果换成两条平行线，那和原来的情况本质上差别不大，轨迹仍然是两条线段之间的一条平行直线。那如果保留其中一个点 $O_1$，把另一个点 $O_2$ 替换为一条固定的直线 $l$2，问题就变成了：所有满足 “到某个固定点和某条固定直线的距离相等” 的点 $P$，它们的轨迹会是什么样的图形？

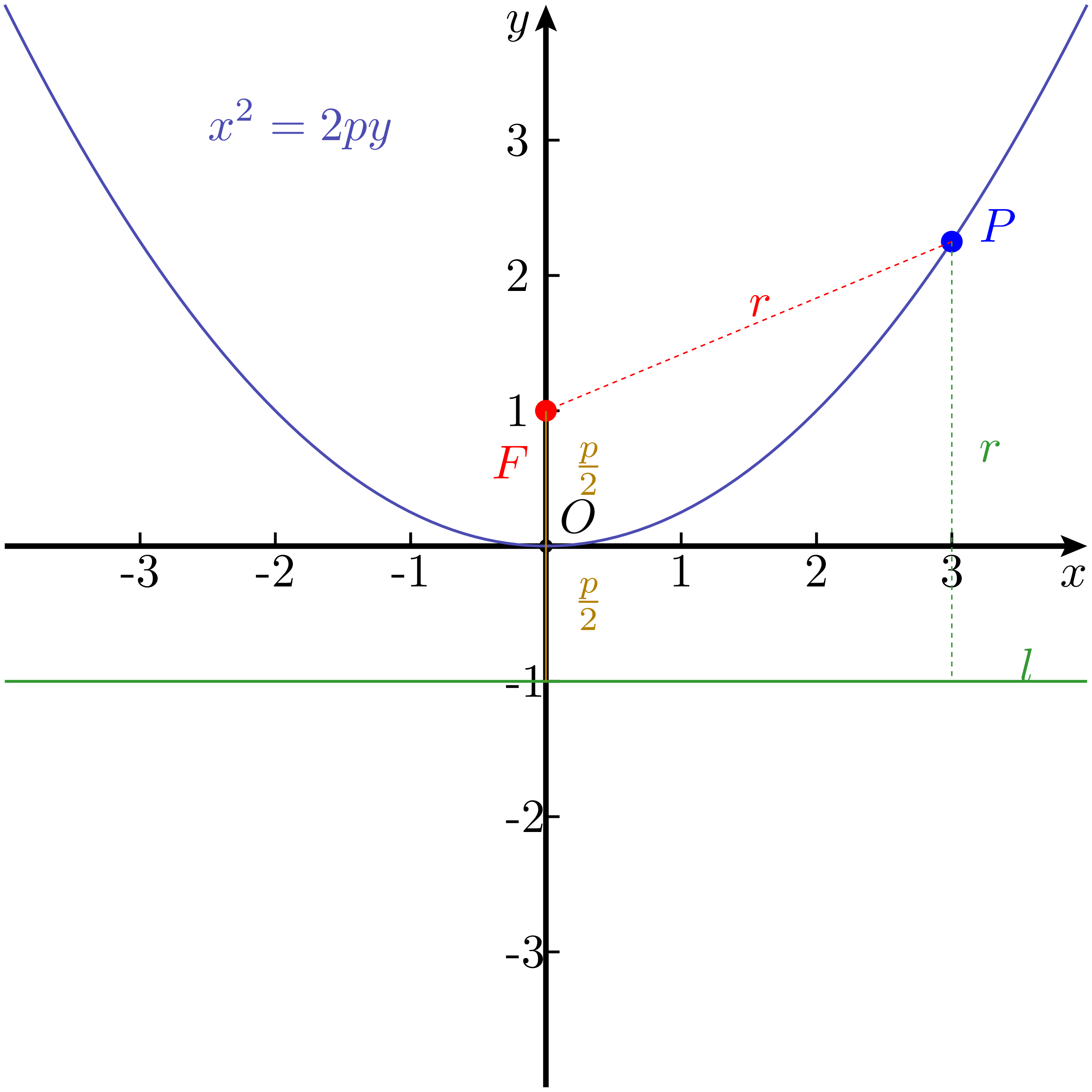
　　 当然，这样修改之后还需要修改 $d$，否则如果直线 $l$ 正好通过定点 $O_1$，唯一满足条件的点就只有 $O_1$，轨迹会退化成一个点。当令 $d$ 满足 $d(O_1,l)=p,(p\neq0)$ 时，情况就变得有趣起来。

例 1　对定点 $F\left(0, \displaystyle\frac{p}{2}\right)$ 和 $l:y=-\displaystyle\frac{p}{2},\left(p>0\right)$，若点 $P$ 满足 $|PF|=d(P,l)$，求点 $P$ 的轨迹方程。

　　 解：

　　 设点 $P$ 的坐标为 $(x, y)$，题设条件表示点 $P$ 到定点 $F$ 的距离等于它到直线 $l$ 的距离。写成数学表达式为：

\begin{equation} \sqrt{x^2 + \left(y - \frac{p}{2}\right)^2} = |y + \frac{p}{2}|~. \end{equation}

　　 两边平方后，展开并整理，利用平方差公式，有：

\begin{equation} x^2 = \left(y + \frac{p}{2}\right)^2 - \left(y - \frac{p}{2}\right)^2 = 2py~. \end{equation}

图
图 1：例 1

　　 可以注意到，原点正好是定点 $F$ 到直线 $l$ 所作垂线段的中点。将式 2 改写为 $y$ 关于 $x$ 的函数形式，可得：

\begin{equation} y = \frac{1}{2p}x^2~. \end{equation}

　　 这个式子正是一个开口向上的二次函数，其图像是顶点在原点、对称轴为 $y$ 轴的曲线。换句话说，从 “点到定点的距离等于它到定直线的距离” 这一条件出发，所得到的轨迹，恰好就是一条抛物线。事实上，这个条件本身也就是抛物线的定义。

定义 1　抛物线

　　 在平面上，所有满足到一条直线 $l$ 与该直线外一固定点 $F$ 的距离相等的点 $P$ 的轨迹，构成一个几何图形，称为抛物线（parabola）。即，对于抛物线上的任意一点 $P$，都有：

\begin{equation} |PF| = d(P, l)~. \end{equation}
其中，$F$ 被称为抛物线的焦点（focus），$l$ 被称为抛物线的准线（directrix），而焦点与准线之间的距离 $d(F, l)$ 被称为抛物线的焦准距（focal parameter），记作 $p$。

　　 根据初中所学，抛物线具有一条对称轴和一个顶点。结合几何定义来看，对称轴（axis of symmetry）是指过焦点并垂直于准线的直线，而顶点（vertex）则是焦点到准线所作垂线段的中点。在抛物线所分割的平面中，约定包含焦点的一侧为抛物线的内部，而包含准线的一侧为其外部。

　　 虽然所有的二次函数图像都是抛物线，但从几何角度来看，抛物线的形状并不取决于它在坐标系中的具体位置。图像放在哪里只会影响它的代数表达式，而不会改变它的几何特征。事实上，任何抛物线都可以通过平移或旋转，化为顶点在原点、对称轴与 $x$ 轴或 $y$ 轴重合的标准形式。因此，在高中阶段的学习中，通常只研究这种标准位置下的抛物线，以便更方便地进行分析和计算。

　　 根据抛物线的定义，可以推导出一个简单但直观的几何性质：作一条与准线平行的直线 $L$，若 $L$ 与准线位于焦点的两侧，那么对于抛物线上的任意一点 $P$，其到焦点的距离 $r$ 与到直线 $L$ 的距离之和是一个定值；反之，若 $L$ 与准线在焦点同侧，则对于任意一点 $P$，其到焦点的距离 $r$ 与到直线 $L$ 的距离之差的绝对值是一个定值。

图
图 2：抛物线的几何性质

　　 以 $L$ 与准线位于焦点两侧的情形为例，如 图 2 所示，记 $O$ 为抛物线焦点，过点 $P$ 作一条垂直于准线的直线，与准线交于点 $A$，与 $L$ 交于点 $B$。根据抛物线的定义有 $|PA| = |OP|$，因此有：

\begin{equation} |AB|=|PA| +|PB| =|OP| +|PB|~. \end{equation}
线段 $AB$ 的长度是固定的，因此 $|OP| +|PB|$ 的值在点 $P$ 变化时保持不变，恒为常数。同侧证明方法也类似，读者可尝试证明。

2. 抛物线的方程

　　 接下来将以 式 2 为基础，考察处于其他 “标准位置” 的抛物线的方程。首先，若将 例 1 中的定点改设为 $F_1(p,0)$，准线改为 $x = -p$，这相当于将原先的 $x$ 轴与 $y$ 轴互换，得到的表达式为：

\begin{equation} y^2 = 2px~. \end{equation}
其次，依据二次函数的知识，若想改变 式 3 中抛物线的开口方向，只需在二次项前添加负号，即可得到：
\begin{equation} y = -\frac{1}{2p}x^2 \quad \Longrightarrow \quad x^2 = -2py~. \end{equation}
综上，可以归纳出抛物线标准方程。

定理 1　抛物线的标准方程

　　

  • 焦点在 $y$ 轴正半轴上的抛物线标准方程：
    \begin{equation} x^2=2py,\qquad(p>0)~. \end{equation}
  • 焦点在 $y$ 轴负半轴上的抛物线标准方程：
    \begin{equation} x^2=-2py,\qquad(p>0)~. \end{equation}
  • 焦点在 $x$ 轴正半轴上的抛物线标准方程：
    \begin{equation} y^2=2px,\qquad(p>0)~. \end{equation}
  • 焦点在 $x$ 轴负半轴上的抛物线标准方程：
    \begin{equation} y^2=-2px,\qquad(p>0)~. \end{equation}

　　 有些读者可能认为无需区分这四种标准方程，只需记住两种基本形式，再根据 $p$ 的正负来判断开口方向，同时将 $|p|$ 理解为抛物线的焦准距。这种记忆方式是可以接受的。不过，在教材中通常采用如上所示的四种形式，是因为参数 $p$ 并不仅出现在此处。为保持定义和表达的一致性，避免在后续内容中引起混淆，故约定 $p$ 为正，通过符号体现抛物线的开口方向。

　　 定理 1 中的四个标准方程，分别对应图 图 3 中开口向上、向下、向右、向左的四种抛物线情形。

图
图 3：标准抛物线

　　 此外，抛物线当然还可以使用参数方程来描述，它本身的关系比较简单，形式上也容易理解。

定理 2　抛物线的参数方程

  • 焦点在 $y$ 轴正半轴上的抛物线参数方程：
    \begin{equation} \begin{cases} x = 2pt \\ y = 2pt^2 \end{cases},\qquad t \in \mathbb{R}~. \end{equation}
  • 焦点在 $y$ 轴负半轴上的抛物线参数方程：
    \begin{equation} \begin{cases} x = -2pt \\ y = -2pt^2 \end{cases},\qquad t \in \mathbb{R}~. \end{equation}
  • 焦点在 $x$ 轴正半轴上的抛物线参数方程：
    \begin{equation} \begin{cases} x = 2pt^2 \\ y = 2pt \end{cases},\qquad t \in \mathbb{R}~. \end{equation}
  • 焦点在 $x$ 轴负半轴上的抛物线参数方程：
    \begin{equation} \begin{cases} x = -2pt^2 \\ y = -2pt \end{cases},\qquad t \in \mathbb{R}~. \end{equation}

　　 以 式 12 为例，当参数 $t$ 从负变为正时，对应的点沿着抛物线从左侧向右侧移动。这种形式能更方便地反映点在轨迹上的运动过程。在具体问题中，还可以根据需要对参数方程进行适当调整，以适配不同方向或位置的抛物线。

抛物线族

　　 与椭圆或双曲线可以通过两个独立的参数分别控制 $x$、$y$ 方向的变化不同，标准形式的抛物线只由一个参数 $p$ 控制其开口程度。如果希望改变抛物线对称轴的方向，不能通过调整参数值实现，而需要通过改变二次项所对应的变量，也就是修改变量的名称来完成。从 “族” 的角度看，所有对称轴相同，仅参数 $p$ 不同的抛物线可以看作是一个抛物线族。

　　 比较特别的是，所有抛物线在几何上彼此都是相似图形。这一点与椭圆和双曲线有本质区别。对于椭圆和双曲线，只有当参数满足一定比例关系时，图形之间才可能相似3。

　　 这一特性也容易证明。设有两个开口方向一致、对称轴为 $x$ 轴的抛物线，其对应参数为 $p_1$ 与 $p_2$，记 $\displaystyle k = \frac{p_1}{p_2}$，则只需在 $x$ 方向保持不变、在 $y$ 方向作 $k$ 倍伸缩，就可将一个抛物线变换为另一个。而若两个抛物线的对称轴不重合，只需先将其通过旋转调整至相同方向，再作适当的缩放，即可实现重合。

　　 这说明，任意两个抛物线都可以通过相似变换（包括旋转与缩放）相互转化，因此在几何意义上，所有抛物线都是相似的图形。

3. 抛物线的几何性质

　　 首先来回答最开始提到的问题，抛物线与双曲线最大的区别是，抛物线没有渐近线。以 式 10 为例，设抛物线上的点为 $P(x, \sqrt{2px})$，考虑任意一条直线 $L: y = ax + b$，分析当 $x \to +\infty$ 时，点 $P$ 到直线 $L$ 的距离变化情况：

\begin{equation} \begin{split} \lim_{x \to +\infty} d(P, L) &= \lim_{x \to +\infty} \frac{|ax - \sqrt{2px} + b|}{\sqrt{a^2 + 1}}\ &= \frac{1}{\sqrt{a^2 + 1}} \lim_{x \to +\infty} | \sqrt{x} \left( a\sqrt{x} - \sqrt{2p} \right) + b |~. \end{split} \end{equation}

　　 从结果可以看出，随着 $x$ 的增大，分子部分 $|ax - \sqrt{2px} + b|$ 也趋于无穷，因此距离不收敛于 $0$。这说明任意一条直线都无法与抛物线无限接近，也就意味着抛物线没有渐近线。这是抛物线与双曲线在图像性质上的一个最显著区别。

切线

　　 先看切线的斜率，一方面对式 3 求导可知：

\begin{equation} y'={p\over x}~. \end{equation}
另一方面，对式 6 ，由隐函数求导可知：
\begin{equation} 2y'y=2p\implies y'={p\over y}~. \end{equation}
参数为负时同样处理即可。这里务必注意 $p$ 在分子上。

　　 根据式 17 和式 18 分别代入式 3 和式 6 得到切线方程：

\begin{equation} y-y_0={x_0\over p}(x-x_0)\quad\implies\quad x_0x=2p\left(\frac{y+y_0}{2}\right)~. \end{equation}
\begin{equation} y-y_0={p\over y_0}(x-x_0)\quad\implies\quad y_0y=2p\left(\frac{x+x_0}{2}\right)~. \end{equation}
这个结果很有趣，与之前椭圆、双曲线的切线形式类似，二次项需要将其中一个变量替换为点的坐标。而特别的是，一次项部分则需要替换成 “点与变量的均值”4。

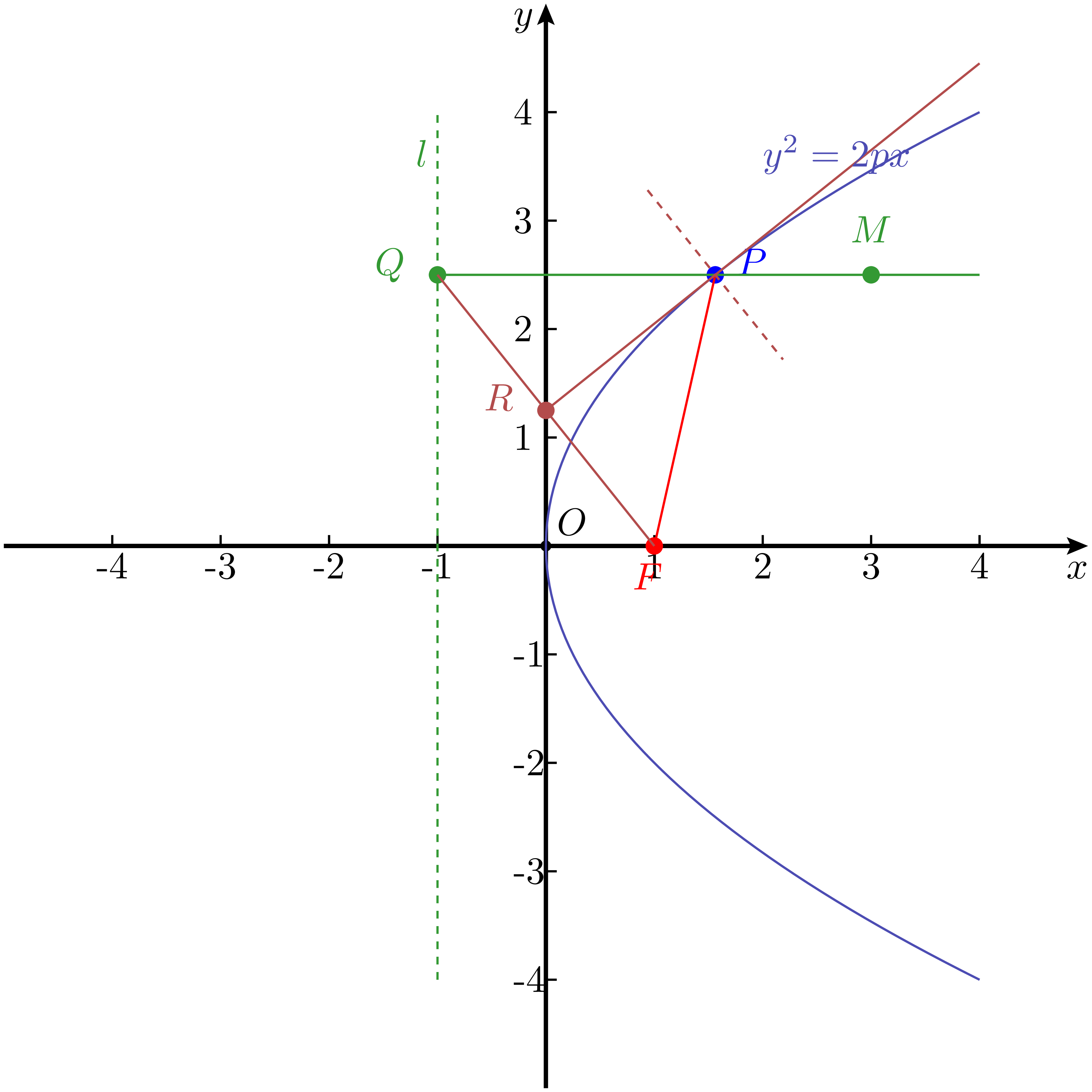
抛物线的反射性质

定理 3　抛物线反射性质

　　 设抛物线的焦点为 $F$，准线为 $l$，点 $P$ 是抛物线上的任意一点。过点 $P$ 作直线 $l$ 的垂线 $m$，则线段 $FP$ 所在直线与 $m$ 关于点 $P$ 处的切线 $n$ 对称。即：

\begin{equation} \angle(FP, n) = \angle(m, n)~. \end{equation}

　　 这一性质说明：若从焦点 $F$ 发出一条光线射向抛物线上任意一点 $P$，该光线在 $P$ 处发生镜面反射后，将沿与准线垂直的方向传播（即平行于对称轴）。反之，若一束与对称轴平行的光线射向抛物线并在点 $P$ 处反射，则反射光线将通过焦点 $F$。也就是说，抛物线能够将来自焦点的光线反射为平行光线，或者将平行光线汇聚到焦点。这正是抛物线在探照灯、雷达天线、太阳能集热器等装置中广泛应用的理论基础。

　　 这个结论其实并不难证明。设抛物线的方程为 $y^2 = 2px$，则其焦点为 $\displaystyle F\left(\frac{p}{2}, 0\right)$，准线为 $\displaystyle l: x = -\frac{p}{2}$。在抛物线上取一点 $P(x_0, y_0)$，连接 $PF$，并作 $P$ 到准线 $l$ 的垂线，垂足记作 $Q\left( \displaystyle -\frac{p}{2}, y_0 \right)$。

图
图 4：抛物线的反射性质示意图

　　 根据抛物线的定义，有：

\begin{equation} |FP| = |PQ|~. \end{equation}
也就是说，$\triangle PQF$ 是一个等腰三角形。设 $R$ 为底边 $FQ$ 的中点，根据中点公式，$R$ 的坐标为 $\displaystyle \left( 0, \frac{y_0}{2} \right)$。由等腰三角形的性质可知，$PR$ 是 $\angle FPQ$ 的角平分线，换句话说，$PF$ 和 $PQ$ 关于 $PR$ 对称。

　　 根据式 18 ，点 $P$ 处抛物线的切线为：

\begin{equation} y-y_0={p\over y_0}(x-x_0)~. \end{equation}
将 $x = 0$ 代入切线方程，并结合抛物线方程 $y_0^2 = 2px_0$ 进行化简，得到 $y$ 轴截距：
\begin{equation} \begin{split} y&=y_0-{px_0\over y_0}\\ &=y_0-{y_0^2\over 2}\cdot{1\over y_0}\\ &={y_0\over 2}~. \end{split} \end{equation}
因此，这条切线恰好通过点 $R$，即 $PR$ 是点 $P$ 处的切线。而前面已经知道 $PF$ 和 $PQ$ 关于 $PR$ 对称，于是可以得出结论——抛物线上的任意一点，其到焦点的连线与到准线的垂线，关于该点的切线对称。

1. ^ 其实还可以换一种方式来看：此时也可以理解为 $\displaystyle \frac{|O_1P|}{|O_2P|} = 1$，然后将定义推广为这个比值为任意常数 $k$，就会得到一种新的轨迹，这类图形被称为阿波罗尼斯圆（Apollonius circle）。
2. ^ 之所以可以进行这样的替换，其实是因为在射影几何的视角下，点和线之间是可以互相转换的。具体内容可参见 圆锥曲线的统一定义。
3. ^ 对于椭圆，是长轴与短轴的比例相同；对于双曲线，是渐近线的夹角相同。这个比例对应着一个非常重要的参数：离心率，参见圆锥曲线的统一定义
4. ^ 这个规律是标准形式下的一个特例，在一些非标准形式或更高次幂的情况下，不能直接套用。感兴趣的读者可以尝试自行推导。


致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。

                     

友情链接： 超理论坛　|　©小时科技 保留一切权利