氢原子隧道电离

贡献者： addis

预备知识　薛定谔方程，隧道效应

　　¹本文使用原子单位制。在 $E \ll 1$ 的恒定电场下，氢原子的电离率（单位时间的概率）为

\begin{equation} \omega = \frac{4}{ \left\lvert E \right\rvert } \exp\left[-\frac{2}{3 \left\lvert E \right\rvert }\right] ~. \end{equation}

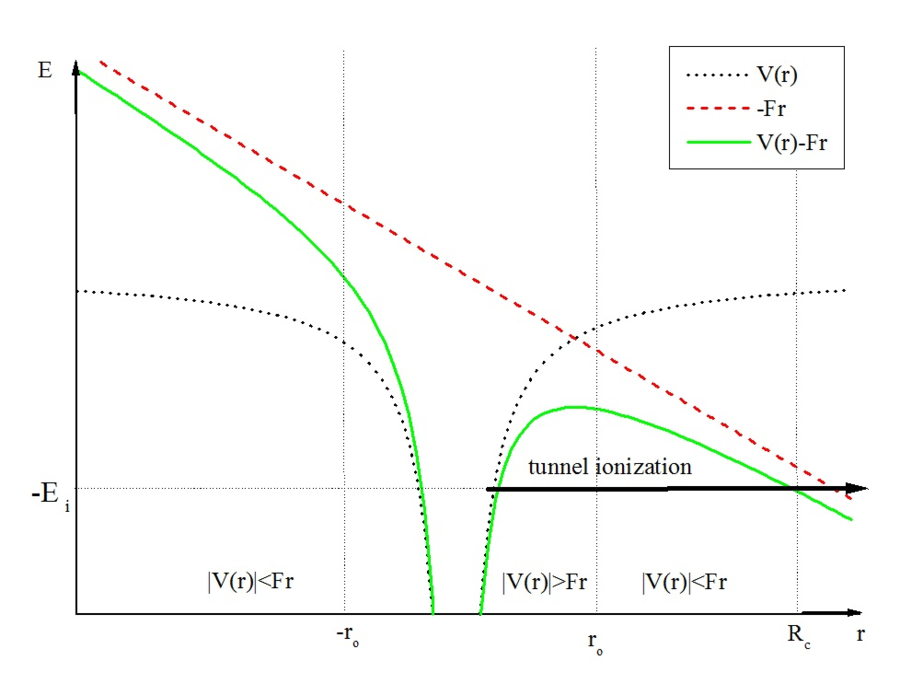
　　注意若给氢原子的哈密顿算符添加恒定电场项 $ \boldsymbol{\mathbf{E}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} $，那么该系统将不存在严格的束缚态。因为当 $ \boldsymbol{\mathbf{r}} $ 和 $ \boldsymbol{\mathbf{E}} $ 夹角大于 $90^\circ$ 且当 $r\to\infty$ 时 $ \boldsymbol{\mathbf{E}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} \to -\infty$（图 1 ）。所以隧道电离不存在严格的阈值（threshold），理论上任何强度的恒定电场都会产生隧道电离。

图 1：隧道电离示意图

　　假设氢原子开始时处于某束缚态且无外电场，能量为 $E_n$，经过一段时间后外电场出现（图中向左），这时在原子核的右边就可能会出现一个势垒，局部势能大于 $E_n$，但随着 $r$ 增大势能最终小于 $E_n$。这时根据隧道效应，波函数会以一定的速率穿过该势垒，单位时间穿过势垒的波函数的概率就叫做电离率（ionization rate）。电场越弱，势垒越高越宽，电离率就越小。

图 2：氢原子隧道电离的数值模拟（见“球坐标系中的定态薛定谔方程”）

　　图 2 中画出了氢原子隧道电离的数值模拟结果，电场方向向上，强度为 0.1 au，图中的数值代表波函数模长的平方，也就是电子在空间中出现的概率（colorbar 使用 log10）。

　　相反，若电场太强，使得右边的势能突起比 $E_n$ 要小，那么同样不存在隧道效应，而是直接电离。这种电离十分迅速。

　　另见ADK 电离率，Keldish 模型（未完成）。

1. ^ 参考 Wikipedia 相关页面。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。