贡献者: addis
预备知识 1 氦原子数值解 TDSE
,库仑波函数
,全同粒子
1. 氦原子基本数据
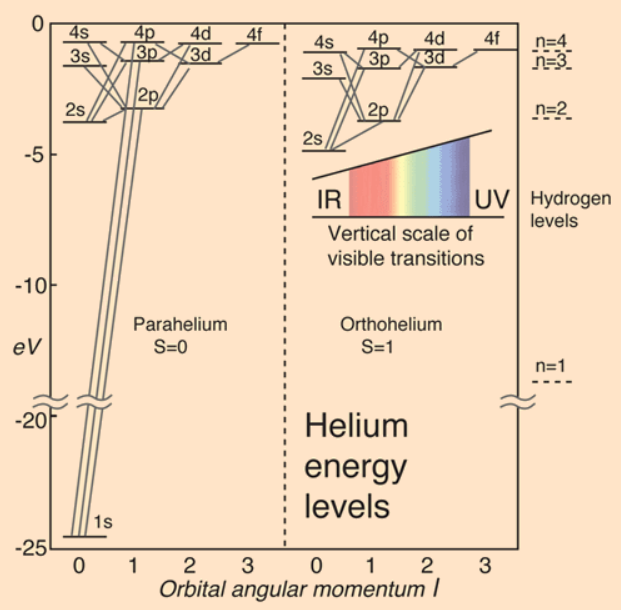
- parahelium: singlet spin ($l_s=0$), 对称波函数,存在 1s 基态(我们使用的)。orthohelium: triplet spin ($l_s=1$), 反对称波函数,不存在 1s 基态,但其他束缚态的能量相对较低。GPT 说标准情况下 ortho 大约是 para 的 3 倍?
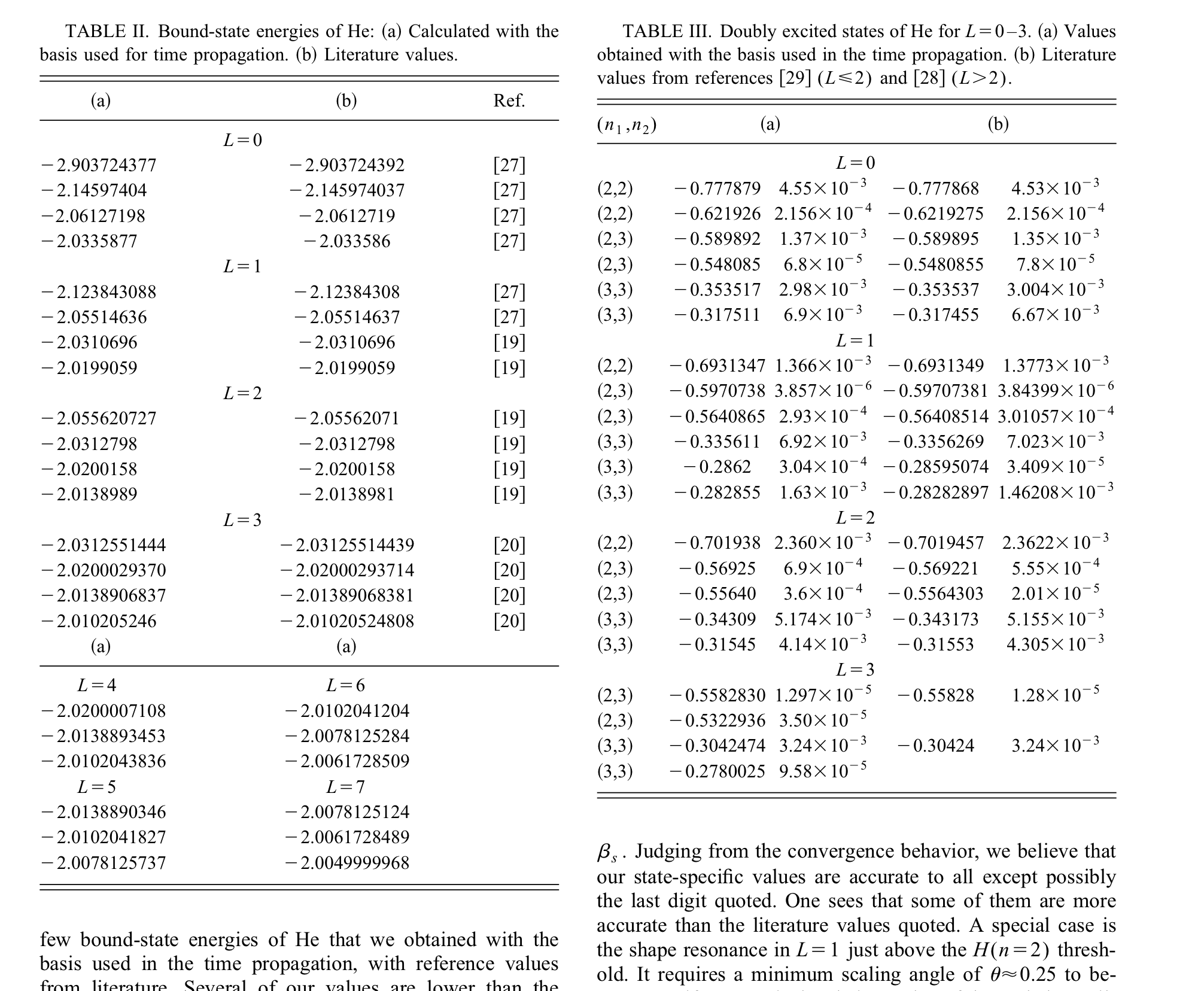
- 基态能量(数值计算):-2.9037244au(-79.014366 eV)
- 1s2s 能量:-2.14597,1s3s 能量:-2.06127,1s4s 能量:-2.03359(参考 Feist 毕业论文)
- 氦离子基态能量:-2au(-54.422772eV)第一激发态 -0.5au(-13.605693eV)第二激发态 -2/9=-0.22...au(-6.0469747eV)
- direct(n=1)单电离 threshold:0.9037244au(24.591594eV)
- shakeup(n=2)单电离 threshold:2.4037244au(65.408673eV)
- shakeup(n=3)单电离 threshold:2.68150218au(72.967391eV)
图 2:能级(Scri98)
90eV XUV 电离
- 90eV 的 xuv 光子能量为 3.3074390au
- 90eV xuv 的 direct(n=1)电离后电子的末动能为 2.4037146au(65.408405eV),末动量为 2.1925850au
- 90eV xuv 的 shakeup(n=2)电离后电子末动能为 0.9037146au(24.591326eV),末动量为 1.3444066au
- 90eV xuv 的 shakeup(n=3)电离后电子末动能为 0.62593682au(17.032608eV),末动量为 1.1188716au
2. 能量
用虚时间法得到基态了以后,我们可以用平均能量来计算基态能量
\begin{equation}
E = \left\langle \Psi \middle| H_0 \middle| \Psi \right\rangle ~.
\end{equation}
3. 动量谱(6 维)
这里考虑的是双电离,因为我们将要把两个电子都投影到连续态,如果任何一个电子处于基态,那么投影将为 0。氢原子的散射态是库仑波函数,而氦原子的(双电子)散射态没有解析解,于是就假设时间足够大时,两电子间没有相互作用,就可以直接把两个库仑波函数做张量积再对称/反对称化即可。而这样一来,散射态和束缚态之间显然就不正交了,所以分析时需要将所有束缚态去掉1。爱华的方法是直接减去基态的投影,然而这样一来激发态的分量就仍然存在了。我认为如果电离波包和未电离的波包已经分离的话,可以像做氢原子那样直接把一定半径内的波函数直接挖掉。
库仑波函数(见式 11 ,我们只需要平面波出射)为($\eta = -mZ/k$,$Z = 2$)
\begin{equation}
\psi_{ \boldsymbol{\mathbf{k}} }( \boldsymbol{\mathbf{r}} ) = \sqrt{\frac{2}{\pi}}\sum_{l, m} \frac{ \mathrm{i} ^l}{r k} \mathrm{e} ^{- \mathrm{i} \sigma_l(\eta)} F_l (\eta, kr) Y_{l, m}^* ( \hat{\boldsymbol{\mathbf{k}}} ) Y_{l, m}( \hat{\boldsymbol{\mathbf{r}}} )~.
\end{equation}
令对称化算符为
\begin{equation}
\hat{S} f( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) = \frac{1}{\sqrt{2}} \left[f( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) + f( \boldsymbol{\mathbf{r}} _2, \boldsymbol{\mathbf{r}} _1) \right] ~.
\end{equation}
那么对称化的散射态为
\begin{equation} \begin{aligned}
& \qquad \psi_{ \boldsymbol{\mathbf{k}} _1, \boldsymbol{\mathbf{k}} _2}( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) = \hat{S} \left[\psi_{ \boldsymbol{\mathbf{k}} _1}( \boldsymbol{\mathbf{r}} _1)\psi_{ \boldsymbol{\mathbf{k}} _2}( \boldsymbol{\mathbf{r}} _2) \right] \\
&= \hat{S} \frac{2}{\pi} \sum_{l_1, m_1} \sum_{l_2, m_2} \frac{ \mathrm{i} ^{l_1 + l_2}}{r_1 r_2 k_1 k_2} \times\\
&\qquad [ \mathrm{e} ^{- \mathrm{i} [\sigma_{l_1}(\eta_1) + \sigma_{l_2} (\eta_2)]} F_{l_1} (\eta_1, k_1 r_1) F_{l_2}(\eta_2, k_2 r_2) Y_{l_1, m_1}^* ( \hat{\boldsymbol{\mathbf{k}}} _1) Y_{l_2, m_2}^* ( \hat{\boldsymbol{\mathbf{k}}} _2)]\times\\
& \qquad Y_{l_1, m_1} ( \hat{\boldsymbol{\mathbf{r}}} _1) Y_{l_2, m_2} ( \hat{\boldsymbol{\mathbf{r}}} _2)~.
\end{aligned} \end{equation}
波函数(假设已经满足交换对称)为
\begin{equation} \begin{aligned}
&\Psi( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) = \sum_{L, M, l_1, l_2} \frac{1}{r_1 r_2} \psi_{l_1, l_2}^{L, M}(r_1, r_2)\mathcal{Y}_{l_1, l_2}^{L, M}( \hat{\boldsymbol{\mathbf{r}}} _1, \hat{\boldsymbol{\mathbf{r}}} _2)\\
& \quad = \sum_{L, M, l_1, l_2} \frac{1}{r_1 r_2} \psi_{l_1, l_2}^{L, M}(r_1, r_2) \sum_{m_1, m_2} \begin{bmatrix}l_1 & l_2 & L\\ m_1 & m_2 & M\end{bmatrix} Y_{l_1, m_1} ( \hat{\boldsymbol{\mathbf{r}}} _1) Y_{l_2, m_2} ( \hat{\boldsymbol{\mathbf{r}}} _2)~.
\end{aligned} \end{equation}
投影得(过程略,对称化算符变为 $\sqrt{2}$,两个 $Y_{l_1, m_1} ( \hat{\boldsymbol{\mathbf{r}}} _1) Y_{l_2, m_2} ( \hat{\boldsymbol{\mathbf{r}}} _2)$ 项积分会产生 2 个 $\delta$ 函数)
\begin{equation}
\left\langle \psi_{ \boldsymbol{\mathbf{k}} _1, \boldsymbol{\mathbf{k}} _2} \middle| \Psi \right\rangle = \frac{2\sqrt 2}{\pi k_1 k_2} \sum_{L, M, l_1, l_2} (- \mathrm{i} )^{l_1 + l_2} \mathrm{e} ^{ \mathrm{i} [\sigma_{l_1}(\eta_1) + \sigma_{l_2} (\eta_2)]} I_{l_1, l_2}^{L, M}(k_1, k_2) \mathcal{Y}_{l_1, l_2}^{L, M}( \hat{\boldsymbol{\mathbf{k}}} _1, \hat{\boldsymbol{\mathbf{k}}} _2)~.
\end{equation}
其中
\begin{equation}
I_{l_1, l_2}^{L, M}(k_1, k_2) = \int_0^\infty \int_0^\infty F_{l_1} (\eta_1, k_1 r_1) F_{l_2}(\eta_2, k_2 r_2) \psi_{l_1, l_2}^{L, M}(r_1, r_2) \,\mathrm{d}{r_1} \,\mathrm{d}{r_2} ~.
\end{equation}
投影的平方就是动量分布
\begin{equation}
P( \boldsymbol{\mathbf{k}} _1, \boldsymbol{\mathbf{k}} _2) = \left\lvert \left\langle \psi_{ \boldsymbol{\mathbf{k}} _1, \boldsymbol{\mathbf{k}} _2} \middle| \Psi \right\rangle \right\rvert ^2~.
\end{equation}
如果固定两个矢量的方向,就可以画出一个二维动量/能量分布图了(注意要乘 $k_1^2k_2^2$)。
4. 径向概率分布
\begin{equation}
P(r_1, r_2) = 2\iint \left\lvert \Psi( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) \right\rvert ^2 r_1^2 r_2^2 \,\mathrm{d}{\Omega_1} \,\mathrm{d}{\Omega_2} ~.
\end{equation}
类比氢原子的情况(
式 15 ),令 $\lambda$ 代表 $l_1, l_2, L, M$
\begin{equation}
\begin{aligned}
& \quad \iint P(r_1, r_2) \,\mathrm{d}{r_1} \,\mathrm{d}{r_2} \\
&= \iint 2\iint \left\lvert \frac{1}{r_1 r_2} \sum_\lambda \psi_\lambda(r_1, r_2) \mathcal{Y}_\lambda ( \hat{\boldsymbol{\mathbf{r}}} _1, \hat{\boldsymbol{\mathbf{r}}} _2) \right\rvert ^2 \,\mathrm{d}{\Omega_1} \,\mathrm{d}{\Omega_2} r_1^2 r_2^2 \,\mathrm{d}{r_1} \,\mathrm{d}{r_2} \\
&= \iint 2\sum_\lambda \left\lvert \psi_\lambda(r_1, r_2) \right\rvert ^2 \,\mathrm{d}{r_1} \,\mathrm{d}{r_2} = 2~,
\end{aligned} \end{equation}
所以
\begin{equation}
P(r_1, r_2) = 2\sum_\lambda \left\lvert \psi_\lambda(r_1, r_2) \right\rvert ^2~.
\end{equation}
这就是 $(r_1, r_2)$ 子空间中的总模长,等于子空间中每个基底的系数的模方和。
5. 能量分布
先继续考虑双电离,式 8 中的概率归一化为(因为对全空间积分重复计算了)
\begin{equation}
\int P( \boldsymbol{\mathbf{k}} _1, \boldsymbol{\mathbf{k}} _2) \cdot k_1^2 \,\mathrm{d}{\Omega_{k1}} \,\mathrm{d}{k_1} \cdot k_2^2 \,\mathrm{d}{\Omega_{k2}} \,\mathrm{d}{k_2} = 2~.
\end{equation}
所以动量绝对值的分布函数为
\begin{equation}
P(k_1, k_2) = k_1^2 k_2^2 \int P( \boldsymbol{\mathbf{k}} _1, \boldsymbol{\mathbf{k}} _2) \,\mathrm{d}{\Omega_{k1}} \,\mathrm{d}{\Omega_{k2}} ~.
\end{equation}
能量分布函数为
\begin{equation}
P(E_1, E_2) = \frac{1}{k_1 k_2} P(k_1, k_2)~,
\end{equation}
所以只需要将
式 8 代入
式 13 得
\begin{equation}
P(k_1, k_2) = \frac{8}{\pi^2} \sum_{L, M, l_1, l_2} \left\lvert I_{l_1, l_2}^{L, M} (k_1, k_2) \right\rvert ^2~.
\end{equation}
其实该式的推导大可直接用球面波而不是投影到平面波再做角向积分,过程类比
氢原子。
6. 双电离概率和截面
双电离总概率为
\begin{equation}
P_{DI} = \frac{1}{2}\int P(k_1, k_2) \,\mathrm{d}{k_1} \,\mathrm{d}{k_2} = \frac{1}{2}\int P(k_1, k_2) \,\mathrm{d}{k_1} \,\mathrm{d}{k_2} ~.
\end{equation}
这里有一个假设就是两个库仑函数的张量积空间就是双电离的本征态空间,即双电子库仑函数所在的空间。这从物理直觉上应该是成立的,但不知如何证明。
下面计算单频截面或微分截面。类比单电子截面的推导,令双电离过程中从波包中单位频率吸收的能量为
\begin{equation}
\frac{\mathrm{d}{\bar E}}{\mathrm{d}{\omega}} = \sigma_j(\omega) s(\omega)~.
\end{equation}
其中 $\sigma_j(\omega)$ 是单频双电离截面。
双电离从电磁波包吸收的总能量为
\begin{equation}
\begin{aligned}
\bar E &= \frac12 \iint \frac{\partial^2 \sigma_j}{\partial \Omega_1 \partial \Omega_2} s(\omega) \,\mathrm{d}{\Omega_1} \,\mathrm{d}{\Omega_2} \,\mathrm{d}{\omega} \\
&= \frac12 \iint \frac{\partial^2 \sigma_j}{\partial \Omega_1 \partial \Omega_2} \frac{s(\omega(k_1,k_2))}{2\pi m} \,\mathrm{d}{\Omega_1} \,\mathrm{d}{\Omega_2} \,\mathrm{d}{k_1} \,\mathrm{d}{k_2} ~.
\end{aligned}
\end{equation}
其中
\begin{equation}
\omega(k_1,k_2) = \frac{k_1^2+k_2^2}{2m} + I_0~.
\end{equation}
并使用了 $\int \,\mathrm{d}{[\pi(k_1^2+k_2^2)]} = \int \,\mathrm{d}{k_1} \,\mathrm{d}{k_2} $。
另一方面,每个原子从 $ \left\lvert j \right\rangle $ 电离平均吸收的能量为
\begin{equation}
\bar E = \frac12 \iint \omega(k_1,k_2) P_j( \boldsymbol{\mathbf{k}} _1, \boldsymbol{\mathbf{k}} _2) k_1^2k_2^2 \,\mathrm{d}{k_1} \,\mathrm{d}{k_2} \,\mathrm{d}{\Omega_1} \,\mathrm{d}{\Omega_2} ~.
\end{equation}
对比
式 18 和
式 20 可以把双电离微分截面表示为
\begin{equation}
\frac{\partial^2 \sigma_j}{\partial \Omega_1 \partial \Omega_2} = \frac{2\pi m \omega}{s(\omega)} \left\langle k_1^2k_2^2 P_j( \boldsymbol{\mathbf{k}} _1, \boldsymbol{\mathbf{k}} _2) \right\rangle ~.
\end{equation}
其中 $ \left\langle \dots \right\rangle $ 是在 $(k_1,k_2)$ 平面的第一象限的由
式 19 定义的四分之一圆上取平均值(线积分后取平均值)。做角向积分得单频截面
\begin{equation}
\sigma_j(\omega) = \frac{2\pi m \omega}{s(\omega)} \left\langle P(k_1,k_2) \right\rangle ~.
\end{equation}
7. JAD(joint angular distribution)
这里的 JAD 并不是总的方向分布,而是某种能量分割的方向分布,即 $k_2 - k_1 = \Delta k$,所以积分中要有一个 delta 函数。
\begin{equation}
\begin{aligned}
P_{JAD}( \hat{\boldsymbol{\mathbf{k}}} _1, \hat{\boldsymbol{\mathbf{k}}} _2) &= \int_0^\infty \int_0^\infty P( \boldsymbol{\mathbf{k}} _1, \boldsymbol{\mathbf{k}} _2) k_1^2 k_2^2 \delta(k_1 - k_2 + \Delta k) \,\mathrm{d}{k_1} \,\mathrm{d}{k_2} \\
&= \frac{8}{\pi^2}\int_0^\infty \int_0^\infty \left\lvert f(k_1, k_2, \hat{\boldsymbol{\mathbf{k}}} _1, \hat{\boldsymbol{\mathbf{k}}} _2) \right\rvert ^2 \delta(k_1 - k_2 + \Delta k) \,\mathrm{d}{k_1} \,\mathrm{d}{k_2} \\
&= \frac{8}{\pi^2} \int_0^\infty \left\lvert f(k_1, k_1 + \Delta k, \hat{\boldsymbol{\mathbf{k}}} _1, \hat{\boldsymbol{\mathbf{k}}} _2) \right\rvert ^2 \,\mathrm{d}{k_1} ~.
\end{aligned}
\end{equation}
其中 $f$ 就是
式 6 中的求和
\begin{equation}
f(k_1, k_2, \hat{\boldsymbol{\mathbf{k}}} _1, \hat{\boldsymbol{\mathbf{k}}} _2) = \sum_{L, M, l_1, l_2} (- \mathrm{i} )^{l_1 + l_2} \mathrm{e} ^{ \mathrm{i} [\sigma_{l_1}(\eta_1) + \sigma_{l_2} (\eta_2)]} I_{l_1, l_2}^{L, M}(k_1, k_2) \mathcal{Y}_{l_1, l_2}^{L, M}( \hat{\boldsymbol{\mathbf{k}}} _1, \hat{\boldsymbol{\mathbf{k}}} _2)~.
\end{equation}
一般在同一平面上取 $ \hat{\boldsymbol{\mathbf{k}}} _1$ 和 $ \hat{\boldsymbol{\mathbf{k}}} _2$($\phi_1 = \phi_2$ 为常数,例如 0),这样就可以画一个横纵坐标分别为 $\theta_1$ 和 $\theta_2$ 的二维分布图 $P_{JAD}(\theta_1, \theta_2)$。
论文中常用一个参数 $\varepsilon$ 来衡量能量分割,定义为较小的光电子末动能与总末动能之比
\begin{equation}
\varepsilon = \frac{\min \left\{E_1, E_2 \right\} }{E_1 + E_2} \qquad (0 \leqslant \varepsilon \leqslant 0.5)~.
\end{equation}
从光子的角度理解 JAD:总能量 $E = k_1^2/2 + k_2^2/2$,再加上 $k_2 - k_1 = \Delta k$ 就把两个光子的能量确定了,剩下的自由度只有角度。但实际上从 $P(k_1, k_2)$ 的图中可以看出,$E = k_1^2/2 + k_2^2/2$ 所表示的圆弧是有宽度的,所以相当于对这个宽度平均了一下。
8. TDCS(triple differential cross section)
类比微分截面的定义,二重微分截面可以定义为
\begin{equation}
\frac{\partial^2\sigma}{\partial\Omega_1\partial\Omega_2} = \frac{1}{n} \int P( \boldsymbol{\mathbf{k}} _1, \boldsymbol{\mathbf{k}} _2)k_1^2k_2^2 \,\mathrm{d}{k_1} \,\mathrm{d}{k_2} ~.
\end{equation}
三重微分截面可以定义为
\begin{equation}
\frac{\partial^3\sigma}{\partial E_1\partial\Omega_1\partial\Omega_2} = \frac{k_1}{n} \int P( \boldsymbol{\mathbf{k}} _1, \boldsymbol{\mathbf{k}} _2)k_2^2 \,\mathrm{d}{k_2} ~.
\end{equation}
爱华的毕业论文中,固定 $ \boldsymbol{\mathbf{k}} _1$,令 $ \boldsymbol{\mathbf{k}} _2$ 在包含 $ \boldsymbol{\mathbf{k}} _1$ 的某平面上旋转,就得到了那个角向分布的实验图。
9. 单光子吸收
类比氢原子吸收一个光子(一阶微扰)后有 $\Delta l = \pm 1$(可以想象成光子带有角动量量子数 1),氦原子从基态吸收一个光子后总角动量也会增加 1。所以要考虑单电子吸收,我们可以只观察 $L = 1$ 的所有分波,甚至在传播时可以用所谓的 “weak field TDSE”2
\begin{equation}
\mathrm{i} \frac{\partial \Psi^{^1P}}{\partial t} = H_0 \Psi^{^1P} + H_E \Psi^{^1S} \mathrm{e} ^{- \mathrm{i} E_0 t}~.
\end{equation}
其中 $H_0$ 是无场的哈密顿,$H_E = E(t) (z_1 + z_2)$ 是电场的哈密顿。
\begin{equation}
\Psi^{^1P}( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2, t) = \sum_{l_1, l_2} \frac{1}{r_1 r_2} \psi_{l_1, l_2}^{1, 0} (r_1, r_2, t) \mathcal Y_{l_1, l_2}^{1, 0} ( \hat{\boldsymbol{\mathbf{r}}} _1, \hat{\boldsymbol{\mathbf{r}}} _2)~,
\end{equation}
吸收一个光子的概率就是对 $L = 1$ 所有分波进行模方积分求和。然而如果做 Streaking 的话,通常会吸收多个红外光子,所以还是需要许多分波。
10. 角向基底变换
除了使用广义球谐函数作为角向基底外,另一个自然的选择就是两个球谐函数的乘积。如果令总波函数为
\begin{equation}
\Psi( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) = \frac{1}{r_1 r_2} \sum_{l_1, m_1, l_2, m_2} \psi_{l_1, l_2}^{m_1, m_2}(r_1, r_2) Y_{l_1, m_1}( \hat{\boldsymbol{\mathbf{r}}} _1) Y_{l_2, m_2} ( \hat{\boldsymbol{\mathbf{r}}} _2)~.
\end{equation}
那么由
式 3 和
式 1 得
\begin{equation}
\psi_{l_1, l_2}^{m_1, m_2}(r_1, r_2) = \sum_{L,M} \begin{bmatrix}l_1 & l_2 & L\\ m_1 & m_2 & M\end{bmatrix} \psi_{l_1, l_2}^{L,M}(r_1, r_2)~.
\end{equation}
若我们有一个 $l_1, l_2, L, M$ 的列表和一个 $l_1, l_2, m_1, m_2$ 的列表,该变换就可以用矩阵表示。
11. 单电子位置分布
由例 2 ,在 $ \boldsymbol{\mathbf{r}} _2$ 位置发现任意一个粒子的概率密度为
\begin{equation}
P( \boldsymbol{\mathbf{r}} _2) = 2\int \left\lvert \Psi( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) \right\rvert ^2 \,\mathrm{d}^{3}{r_1} ~.
\end{equation}
若使用
式 30 形式的波函数
3,这个积分的形式就变得相当简单,先令 $ \boldsymbol{\mathbf{r}} _2$ 为常矢量,计算关于 $r_1$ 的径向波函数
\begin{equation}
\psi_{l_1, m_1}(r_1, \boldsymbol{\mathbf{r}} _2) = \frac{1}{r_2} \sum_{l_2, m_2} \psi_{l_1, l_2}^{m_1, m_2}(r_1, r_2) Y_{l_2, m_2}( \hat{\boldsymbol{\mathbf{r}}} _2)~.
\end{equation}
这样
式 30 就变为
\begin{equation}
\Psi( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) = \frac{1}{r_1} \sum_{l_1, m_1} \psi_{l_1, m_1}(r_1, \boldsymbol{\mathbf{r}} _2) Y_{l_1, m_1} ( \hat{\boldsymbol{\mathbf{r}}} _1)~.
\end{equation}
单电子概率为
\begin{equation}
\begin{aligned}
P( \boldsymbol{\mathbf{r}} _2) &= 2\sum_{l_1, m_1} \int \left\lvert \psi_{l_1, m_1}(r_1, \boldsymbol{\mathbf{r}} _2) \right\rvert ^2 \,\mathrm{d}{r_1} \\
& = \frac{2}{r_2^2} \sum_{l_1, m_1} \int \left\lvert \sum_{l_2, m_2} \psi_{l_1, l_2}^{m_1, m_2}(r_1, r_2) Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{r}}} _2) \right\rvert ^2 \,\mathrm{d}{r_1} ~.
\end{aligned}
\end{equation}
每个 $(n_1,l_1)$ channel 的单电子位置分布
把总波函数 $\Psi( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2)$ 投影到第一个电子的束缚态上,得
\begin{equation}
\begin{aligned}
& \left\langle n_1,l_1,m_1 \middle| \Psi \right\rangle ( \boldsymbol{\mathbf{r}} _2)\\
&= \int R_{n_1, l_1}(r_1) Y_{l_1, m_1}( \hat{\boldsymbol{\mathbf{r}}} _1) \left[\frac{1}{r_1 r_2} \sum_{l_1',m_1'}\sum_{l_2, m_2} \psi_{l'_1,l_2}^{m'_1,m_2}(r_1,r_2) Y_{l'_1,m'_1}( \hat{\boldsymbol{\mathbf{r}}} _1)Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{r}}} _2) \right] r_1^2 \,\mathrm{d}{\Omega_1} \,\mathrm{d}{r_1} \\
&= \frac{1}{r_2}\sum_{l_2,m_2} \left[\int r_1 R_{n_1,l_1}(r_1) \psi_{l_1,l_2}^{m_1,m_2}(r_1,r_2) \,\mathrm{d}{r_1} \right] Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{r}}} _2)\\
&= \frac{1}{r_2}\sum_{l_2,m_2} \psi_{l_2,m_2}^{(n_1,l_1,m_1)}(r_2) Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{r}}} _2)~.
\end{aligned}
\end{equation}
现在对给定的 $(n_1, l_1)$ channel,
\begin{equation}
\Psi_{n_1,l_1}( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) = \sum_{m_1} \left\lvert n_1,l_1,m_1 \right\rangle ( \boldsymbol{\mathbf{r}} _1) \left\langle n_1,l_1,m_1 \middle| \Psi \right\rangle ( \boldsymbol{\mathbf{r}} _2)~,
\end{equation}
\begin{equation}
\begin{aligned}
&P_{n_1,l_1}( \boldsymbol{\mathbf{r}} _2) = \int \left\lvert \Psi_{n_1,l_1}( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) \right\rvert ^2 \,\mathrm{d}^{3}{r_1}
= \sum_{m_1} \left\lvert \left\langle n_1,l_1,m_1 \middle| \Psi \right\rangle ( \boldsymbol{\mathbf{r}} _2) \right\rvert ^2\\
&= \frac{1}{r_2^2} \sum_{m_1} \left\lvert \sum_{l_2,m_2} \psi_{l_2,m_2}^{(n_1,l_1,m_1)}(r_2) Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{r}}} _2) \right\rvert ^2~.
\end{aligned}
\end{equation}
要计算给定方向 $ \hat{\boldsymbol{\mathbf{r}}} _2$ 一个窄圆锥中的 $r_2$ 平均值,就是
\begin{equation}
\left\langle r_2 \right\rangle _{n_1,l_1, \hat{\boldsymbol{\mathbf{r}}} _2} = \frac{\int r_2 P_{n_1,l_1}( \boldsymbol{\mathbf{r}} _2) r_2^2 \,\mathrm{d}{r_2} }{\int P_{n_1,l_1}( \boldsymbol{\mathbf{r}} _2) r_2^2 \,\mathrm{d}{r_2} }
= \frac{\sum_{m_1} \int r_2 \left\lvert \sum_{l_2,m_2} \psi_{l_2,m_2}^{(n_1,l_1,m_1)}(r_2) Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{r}}} _2) \right\rvert ^2 \,\mathrm{d}{r_2} }{\sum_{m_1} \int \left\lvert \sum_{l_2,m_2} \psi_{l_2,m_2}^{(n_1,l_1,m_1)}(r_2) Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{r}}} _2) \right\rvert ^2 \,\mathrm{d}{r_2} }~.
\end{equation}
根据选择定则,$n_1 = 2$ 时共有 5 个分波 $(n_1,l_1,m_1,l_2,m_2) = (2, 0, 0, 1, 0)$,$(2,1,0,0,0)$,$(2,1,0,2,0)$,$(2,1,\pm 1, 2,\mp 1)$。对于 $(n_1, l_1) = (2, 1)$ 共有 4 个分波。若选择 $z$ 方向,$m_1 = -m_2 \ne 0$ 时 $Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{z}}} ) \equiv 0$,所以求和中只有两个分波,但算出来的延迟只是 Pazourek 用 EWS 算出的一半左右。这很可能是因为她的圆锥取了 10° 的张角,而不是假设细圆锥。
12. 单电离动量谱
在 $P(r_1, r_2)$ 分布中,单电离一般是可以与双电离区分开的,只需要取一个 box 即可:$r_1 < r_{1,max}$,$r_2 > r_{2,min}$
\begin{equation}
\left\langle \boldsymbol{\mathbf{r}} _1 \right\rvert \left\langle C_{l_2,m_2}(k_2) \middle| \Psi \right\rangle = \frac{1}{r_1} \sum_{l_1, m_1} \psi_{l_1,m_1}(r_1) \cdot Y_{l_1, m_1}( \hat{\boldsymbol{\mathbf{r}}} _1)~,
\end{equation}
\begin{equation}
\psi_{l_1,m_1}(r_1) = \int_{r_{2,min}}^{+\infty} \sqrt{\frac{2}{\pi}}F_{l_2}(\eta_2, k_2 r_2)\psi_{l_1, l_2}^{m_1, m_2}(r_1, r_2) \,\mathrm{d}{r_2} ~,
\end{equation}
然而 streaking trace 需要的不是上式的概率而是某个方向的概率。我们使用
式 13 做线性组合即可
\begin{equation}
\left\langle \boldsymbol{\mathbf{r}} _1 \right\rvert \langle{\psi_{ \boldsymbol{\mathbf{k}} _2}^{(-)}}|{\Psi}\rangle = \sum_{l_2,m_2} \frac{ \mathrm{i} ^{-l_2}}{k_2} \mathrm{e} ^{ \mathrm{i} \sigma_{l_2}}Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{k}}} _2) \left\langle \boldsymbol{\mathbf{r}} _1 \right\rvert \left\langle C_{l_2,m_2}(k_2) \middle| \Psi \right\rangle ~.
\end{equation}
所以(
式 40 代入
式 42 ,整理成 $1/r_1\sum \dots Y_{l_1,m_1}( \boldsymbol{\mathbf{r}} _1)$ 形式)
\begin{equation}
\begin{aligned}
P( \boldsymbol{\mathbf{k}} _2) &= \int_0^{r_{1,max}} \left\lvert \left\langle \boldsymbol{\mathbf{r}} _1 \right\rvert \langle{\psi_{ \boldsymbol{\mathbf{k}} _2}^{(-)}}|{\Psi}\rangle \right\rvert ^2 \,\mathrm{d}^{3}{r_1} \\
&= \sum_{l_1,m_1} \int_0^{r_{1,max}} \left\lvert \sum_{l_2,m_2} \frac{ \mathrm{i} ^{-l_2}}{k_2} \mathrm{e} ^{- \mathrm{i} \sigma_{l_2}} Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{k}}} _2) \cdot \psi_{l_1,m_1}(r_1) \right\rvert ^2 \,\mathrm{d}{r_1} ~.
\end{aligned}
\end{equation}
13. Shakeup 电离
令归一化的基态为
\begin{equation}
\phi_{n_1, l_1, m_1}( \boldsymbol{\mathbf{r}} _1) = R_{n_1,l_1}(r_1)Y_{l_1,m_1}( \hat{\boldsymbol{\mathbf{r}}} _1)~.
\end{equation}
归一化的散射态为
\begin{equation}
C_{l_2, m_2}(k_2, \boldsymbol{\mathbf{r}} _2) = \frac{1}{r_2}\sqrt{\frac{2}{\pi}} F_{l_2}(\eta_2, k_2 r_2) Y_{l_2, m_2} ( \hat{\boldsymbol{\mathbf{r}}} _2)~.
\end{equation}
以下的计算和单电子概率分布很类似,我们同样不需要太在意粒子交换对称的问题,把内积乘以 $\sqrt{2}$,概率乘以 2 即可。同样先把总波函数转换为
式 30 的形式,投影得到
\begin{equation}
\left\langle \phi_{n_1, l_1, m_1} \right\rvert \left\langle C_{l_2, m_2}(k_2) \middle| \Psi \right\rangle = \sqrt{\frac{2}{\pi}} \iint r_1 R_{n_1,l_1}(r_1) F_{l_2}(\eta_2, k_2 r_2) \psi_{l_1, l_2}^{m_1, m_2}(r_1, r_2) \,\mathrm{d}{r_1} \,\mathrm{d}{r_2} ~.
\end{equation}
然而,streaking trace 需要的不是上式的概率而是某个方向的概率。我们只需使用
式 13 做线性组合即可
\begin{equation}
\left\langle \phi_{n_1, l_1, m_1} \right\rvert \langle{\psi_{ \boldsymbol{\mathbf{k}} _2}^{(-)}}|{\Psi}\rangle = \sum_{l_2,m_2} \frac{ \mathrm{i} ^{-l_2}}{k_2} \mathrm{e} ^{ \mathrm{i} \sigma_{l_2}} Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{k}}} _2) \left\langle \phi_{n_1, l_1, m_1} \right\rvert \left\langle C_{l_2, m_2}(k_2) \middle| \Psi \right\rangle ~,
\end{equation}
\begin{equation}
P(n_1, l_1, m_1, \boldsymbol{\mathbf{k}} _2) = \left\lvert \left\langle \phi_{n_1, l_1, m_1} \right\rvert \langle{\psi_{ \boldsymbol{\mathbf{k}} _2}^{(-)}}|{\Psi}\rangle \right\rvert ^2~.
\end{equation}
当 $M \equiv 0$ 时这里对 $m_2$ 求和其实只有一项就是 $m_2 = - m_1$,也是一个常数。理论上,如果把式 48 对所有 $n_1, l_1, m_1$ 求和,应该和式 43 相等。
考虑探测器的立体角
$P(n_1, l_1, m_1, \boldsymbol{\mathbf{k}} _2)$ 中,探测器实际捕获的是一个立体角为 $\Omega$ 的圆锥中的光电子,如果假设 $\Omega \to 0$,总概率为
\begin{equation}
\int P(n_1, l_1, m_1, \boldsymbol{\mathbf{k}} _2) k_2^2 \Omega \,\mathrm{d}{k_2} ~,
\end{equation}
所以实际测到的光电子动量谱应该是
\begin{equation}
\Omega k_2^2 P(n_1, l_1, m_1, k_2)~.
\end{equation}
14. XUV-only 分波延迟
解析表达式见论文。现在讨论如何从波函数中提取每个 $\gamma = (n_1, l_1, m_1, l_2, m_2)$ 分波的延迟。首先需要使用式 30 的角向基底。投影后得(bra 未对称化)
\begin{equation}
\left\langle n_1,l_1,m_1, \boldsymbol{\mathbf{r}} _2 \middle| \Psi \right\rangle = \frac{1}{r_2} \sum_{l_2,m_2}\psi_\gamma(r_2) Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{r}}} _2)~,
\end{equation}
\begin{equation}
\psi_\gamma(r_2) = \int_0^\infty r_1 R_{n_1,l_1}(r_1) \psi_{l_1,l_2}^{m_1,m_2}(r_1,r_2) \,\mathrm{d}{r_1} ~.
\end{equation}
对某个 $\gamma$ 分波,取
式 51 求和中的一项,单电子分布为
\begin{equation}
P_\gamma( \boldsymbol{\mathbf{r}} _2) = 2 \left\lvert \frac{1}{r_2} \psi_\gamma(r_2) Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{r}}} _2) \right\rvert ^2~,
\end{equation}
径向分布为
\begin{equation}
P_\gamma(r_2) = \int P_\gamma( \boldsymbol{\mathbf{r}} _2) r_2^2 \,\mathrm{d}{\Omega_2} = 2 \left\lvert \psi_\gamma(r_2) \right\rvert ^2~.
\end{equation}
我们既可以选取平均值也可以选取波峰作为某个时候光电子的距离。Pazourek 论文的参数下,二者的区别会有较大的不同,尤其是对于 shakeup。我认为 EWS 延迟的推导使用了驻相法,所以应该用波峰。
如果直接用光子能量计算末动能,那么会发现延迟会随时间线性变化,也就是说光电子实际的末动能并不能直接这么计算,而是需要测量出来。那么假设电离后时间 $t$ 时光电子测到的位置为 $r_c$(平均值或峰值),速度为 $k$,那么根据库仑势能可以预测末速度约等于($ \,\mathrm{d}{k} = \,\mathrm{d}{E} /k$)
\begin{equation}
k_f = k - \frac{1}{rk}~.
\end{equation}
那么匀速运动的参考轨迹为 $r = k_f t$,光电子的延迟满足
\begin{equation}
r_c = k_f(t - t_\text{XUV})~.
\end{equation}
当 $t$ 足够大时,$t_\text{XUV}$ 就会收敛。
15. 单电离的相对延迟分析
Osiander/Pazourek 对延迟的分析的解释是:单电离的瞬间,氦离子存在 electric dipole(几乎不随时间变化),对电离的电子产生了吸引力的作用。但似乎并没有解释如何从波函数画出这个 dipole。
显然,这不能用上述的单电子概率分布来画,因为在当前计算中电离率只有 1e-6 到 1e-5 的数量级。这说明总波函数主要还处于束缚态。我认为正确的方法是计算位置分布 $P( \boldsymbol{\mathbf{r}} _1) = P( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2)$,其中 $ \boldsymbol{\mathbf{r}} _2$ 可以取电离波包的平均位置或者对电离波包的所有位置积分
\begin{equation}
P( \boldsymbol{\mathbf{r}} _1) = \int P( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) \,\mathrm{d}^{3}{r_2} ~.
\end{equation}
或者,也可以计算 $P( \boldsymbol{\mathbf{r}} _1) = P( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{k}} _2)$,其中 $ \boldsymbol{\mathbf{k}} _2$ 取电离波包的中心动量或者对波包的所有动量积分(要确保只包含电离波包)
\begin{equation}
P( \boldsymbol{\mathbf{r}} _1) = \int P( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{k}} _2) \,\mathrm{d}^{3}{k_2} ~,
\end{equation}
又或者对 streaking trace 上的某条竖线的 shakeup 或 direct 区间积分。
\begin{equation}
P( \boldsymbol{\mathbf{r}} _1) = \int P( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{k}} _2) \,\mathrm{d}{k_2} ~.
\end{equation}
我认为最后的做法是最靠谱的,毕竟 streaking trace 是动量谱。
下面讨论如何计算 $P( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{k}} _2)$。可以先将波函数写成
\begin{equation}
\Psi( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) = \frac{1}{r_1}\sum_{l_1,m_1} \left[\frac{1}{r_2}\sum_{l_2,m_2} \psi_{l_1,l_2}^{m_1,m_2}(r_1, r_2) Y_{l_2,m_2}( \hat{\boldsymbol{\mathbf{r}}} _2) \right] Y_{l_1,m_1}( \hat{\boldsymbol{\mathbf{r}}} _1)~.
\end{equation}
中括号中的内容逐项投影到库仑平面波 $ \left\lvert \boldsymbol{\mathbf{k}} _2 \right\rangle $ 上得 $\psi_{l_1,m_1}(r_1)$,按照
式 15 的方法即可。于是
\begin{equation}
P( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{k}} _2) = 2 \left\lvert \frac{1}{r_1}\sum_{l_1,m_1} \psi_{l_1,m_1}(r_1) Y_{l_1,m_1}( \hat{\boldsymbol{\mathbf{r}}} _1) \right\rvert ^2~,
\end{equation}
乘以 2 是考虑了全同粒子。
计算结果:没有看出 dipole,很可能因为计算投影 $\psi_{l_1,m_1}(r_1)$ 的时候原子核附近的电子云贡献了很大一部分。可能需要切除原子核以后再投影才行。
其实切除的话还不如直接计算 $P( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2)$ 分布,保持 $ \boldsymbol{\mathbf{r}} _2$ 不变(可以取光电子波包的正中心)。直接用式 60 的 2 倍模方即可(固定 $ \boldsymbol{\mathbf{r}} _2$)。
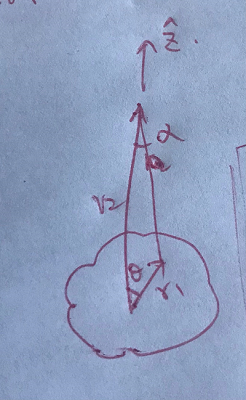
图 3:经典力学计算延迟
用经典电磁学和力学来试图计算延迟:$P( \boldsymbol{\mathbf{r}} _2)$ 位置分布是两个环形的 dipole,外面的环的代表 direct 电离,里面的环代表 shake-up。那我们可以分别取 $ \boldsymbol{\mathbf{r}} 2$ 为 $z$ 方向外环中心和内环中心的位置,在每个时间 $t$ 分别计算两个位置的 $P( \boldsymbol{\mathbf{r}} _1)$ 分布,计算该电荷分布对 $ \boldsymbol{\mathbf{r}} $ 处的引力。然后比较该引力对两个经典力学轨迹的时间延迟只差即可。受力计算(不包含原子核的引力):
\begin{equation}
\begin{aligned}
F_z( \boldsymbol{\mathbf{r}} _2) &=
\int \frac{P( \boldsymbol{\mathbf{r}} _1)}{r_{12}^2} \hat{\boldsymbol{\mathbf{r}}} _{12} \,\mathrm{d}^{3}{r_1} - \frac{1}{r_2^2}\\
&= \iiint \frac{P( \boldsymbol{\mathbf{r}} _1) \cos\alpha}{r_{12}^2} r_1^2\sin\theta_1 \,\mathrm{d}{r_1} \,\mathrm{d}{\theta_1} \,\mathrm{d}{\phi_1} - \frac{1}{r_2^2}~,
\end{aligned}
\end{equation}
\begin{equation}
r_{12}^2 = r_1^2 + r_2^2 - 2r_1r_2 \cos\theta_1~.
\end{equation}
\begin{equation}
\cos\alpha = \frac{r_2^2 + r_{12}^2 - r_1^2}{2r_2 r_{12}}~.
\end{equation}
最后一种方案是:
\begin{equation}
\begin{aligned}
P( \boldsymbol{\mathbf{r}} _1) &= \int_{\mathcal V} P( \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2) \,\mathrm{d}^{3}{r_2} \\
&= \int_a^b \int_0^{\pi/2} \int_0^{2\pi} \left\lvert \sum_{L, M, l_1, l_2} \frac{1}{r_1 r_2} \psi_{l_1, l_2}^{L, M}(r_1, r_2)\mathcal{Y}_{l_1, l_2}^{L, M}( \hat{\boldsymbol{\mathbf{r}}} _1, \hat{\boldsymbol{\mathbf{r}}} _2) \right\rvert ^2 r_2^2\sin\theta_2 \,\mathrm{d}{r_2} \,\mathrm{d}{\theta_2} \,\mathrm{d}{\phi_2} ~,
\end{aligned}
\end{equation}
其中积分范围是 $z+$ 方向的空心半球。这算是一种折衷的办法,也就是光电子往 $z+$ 半球电离时,dipole 分布的平均值。可以通过不同的 $[a, b]$ 来区分不同的 shakeup。
16. EWS 延迟
参考论文草稿。
17. 其他
图 4:估计 $\Delta k$
\begin{equation}
\Delta k_{max} = k_0 \sin\left(2\pi \tau/T_{IR}\right) \approx 2 \pi k_0 \tau/T_{IR}~.
\end{equation}
在 test800 中 $k_0 \approx 0.042$,$\tau = 16$,$T_{IR} = 110.245$。得 $\Delta k_{max} \approx 0.038$。
1. ^ 理论上束缚态不去掉也没关系,因为单电子的库仑球波函数和束缚态本来就是正交的。这么做可能是考虑到数值误差?
2. ^ 参考 Colgan 2001, J Phys. B: 34 (2001) L457-L466
3. ^ 在程序中不一定需要先这么做,只需要将式 31 代入以下各式,在将 $L, M, l_1, l_2$ 的求和提到最外面即可
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。