二体问题（分析力学）

贡献者： _Eden_; addis

预备知识　运动积分，中心力场问题

1. 两体问题的运动方程

　　两体问题研究的对象是两个可以看成质点的物体，质量分别为 $m_1,m_2$，位矢分别为 $ \boldsymbol{\mathbf{r}} _1, \boldsymbol{\mathbf{r}} _2$。它们之间的相互作用势是 $V(r)=V(| \boldsymbol{\mathbf{r}} _1- \boldsymbol{\mathbf{r}} _2|)$，也就是说只和两者的距离有关。开普勒问题、卢瑟福散射都属于两体问题。

　　在这个词条中我们将用分析力学的方法来解决两体问题。设 $ \boldsymbol{\mathbf{r}} _c$ 为质心位置，设 $ \boldsymbol{\mathbf{r}} $ 为它们的相对位置，那么有

\begin{equation} \left\{\begin{aligned} \boldsymbol{\mathbf{r}} _c &=\frac{m_1 \boldsymbol{\mathbf{r}} _1+ m_2 \boldsymbol{\mathbf{r}} _2}{m_1+m_2}~,\\ \boldsymbol{\mathbf{r}} \ &= \boldsymbol{\mathbf{r}} _2- \boldsymbol{\mathbf{r}} _1~. \end{aligned}\right. \end{equation}

那么体系的动能为质心动能加上系统相对于质心参考系的动能。

\begin{equation} \begin{aligned} T&=\frac{1}{2}m_1 \dot{ \boldsymbol{\mathbf{r}} }_1^2+\frac{1}{2}m_2 \dot{ \boldsymbol{\mathbf{r}} }_2^2\\ &=\frac{1}{2}(m_1+m_2)\dot{ \boldsymbol{\mathbf{r}} }_c^2+\frac{1}{2}\frac{m_1m_2}{m_1+m_2}\dot{ \boldsymbol{\mathbf{r}} }^2\\ &=\frac{1}{2}M \dot{ \boldsymbol{\mathbf{r}} }_c^2+\frac{1}{2}\mu \dot{ \boldsymbol{\mathbf{r}} }^2 \end{aligned}~. \end{equation}

其中 $M$ 为体系的总质量，$\mu$ 称作约化质量：

\begin{equation} \left\{ \begin{aligned} &M=m_1+m_2\\ &\mu=\frac{m_1m_2}{m_1+m_2}~. \end{aligned} \right. \end{equation}

在无外界影响的情况下，$\dot{ \boldsymbol{\mathbf{r}} }_c=0$（这是因为系统的动量守恒）。系统的势能为 $V(r)$。因此拉格朗日量为 $L=T(\dot{ \boldsymbol{\mathbf{r}} })-V(r)$。两个物体一定在同一个平面内作运动，设 $ \boldsymbol{\mathbf{r}} $ 在该平面内转过的角度为 $\phi$，设 $| \boldsymbol{\mathbf{r}} |=\rho$。我们取广义坐标 $\rho,\phi$。那么 $T=\frac{1}{2}\mu \dot{ \boldsymbol{\mathbf{r}} }^2=\frac{1}{2}\mu \dot \rho^2+\frac{1}{2}\mu \rho^2\dot\phi^2$。体系的拉格朗日量和哈密顿量为

\begin{equation} \begin{aligned} &L=\frac{1}{2}\mu \dot \rho^2+\frac{1}{2}\mu \rho^2\dot\phi^2-V(\rho)~,\\ &H=T+V=\frac{1}{2}\mu \dot \rho^2+\frac{1}{2}\mu \rho^2\dot\phi^2+V(\rho)~. \end{aligned} \end{equation}

因此可以列出拉格朗日方程：

\begin{equation} \begin{aligned} &\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} }\frac{\partial L}{\partial \dot\rho}=\frac{\partial L}{\partial \rho}\\&\Rightarrow \mu\ddot\rho-\mu\rho\dot\phi^2+\frac{ \,\mathrm{d}{V} }{ \,\mathrm{d}{\rho} }=0~, \end{aligned} \end{equation}

\begin{equation} \begin{aligned} &\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} }\frac{\partial L}{\partial \dot\phi}=\frac{\partial L}{\partial \phi}\\& \Rightarrow \frac{ \,\mathrm{d}{p} _\phi}{ \,\mathrm{d}{t} }=\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{t} }(\mu \rho^2\dot\phi)=0 \\& \Rightarrow p_\phi=\frac{\partial L}{\partial \dot \phi}=\mu\rho^2\dot\phi ={\rm const}=J ~. \end{aligned} \end{equation}

式 5 式 6 联立就可以得到两体问题的运动方程（两个方程和两个初始条件，就可以求解两个广义坐标的变化）。或者我们也可以简化方程组，将其中一个替换为能量守恒方程，联立得：

\begin{equation} \begin{aligned} &\left\{ \begin{aligned} &\frac{1}{2}\mu \left(\dot\rho^2+\rho^2\dot\phi^2 \right) +V(\rho)=E\\ &\mu\rho^2\dot\phi=J \end{aligned} \right.\\ &\Rightarrow \frac{1}{2}\mu \dot\rho^2=E-V(\rho)-\frac{J^2}{2\mu\rho^2}=E-V_{\rm{eff}}(\rho)~. \end{aligned} \end{equation}

$V_{\rm{eff}}=V(\rho)+\frac{J^2}{2\mu\rho^2}$ 为有效势能。从有效势能与能量 $E$ 的大小关系，可以判断体系处于束缚态还是散射态。

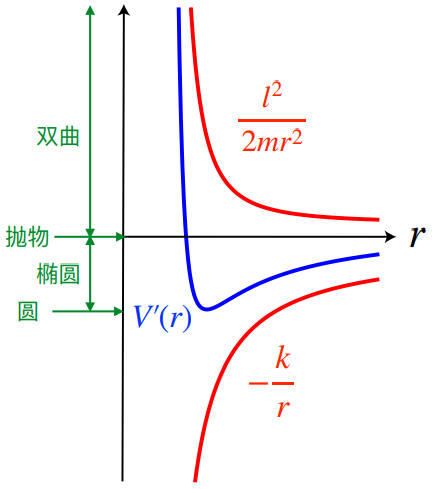
图 1：有效势能（图中蓝线）的函数图像

　　以图 1 为例，对于相互作用势为 $-k/r$ 的两体系统，有效势能 $V_{\rm{eff}}(r)$ 的函数图象如蓝线所示。如果系统的能量 $E$ 恰好等于有效势能极小值（蓝线的最低处），那么系统将作圆周运动；如果 $E<0$，体系处于束缚态，轨道形状为椭圆；如果 $E=0$，那么体系处于散射态，轨道形状为抛物线；如果 $E>0$，那么体系处于散射态，轨道形状为双曲线。轨道形状是二次曲线的原因，与相互作用势 $V=-k/r$ 有关。

　　从上面的运动方程式 7 可以求解出 $\rho$ 关于 $t$ 的函数；然而具体要解出轨道形状，还需要知道 $\phi$ 关于 $t$ 的函数，这就又需要借助角动量守恒方程。为了快速求出轨道形状，我们通常令 $u=1/\rho$ 对上面的式 7 进行化简。注意到 $\dot u=-\dot \rho/\rho^2=\mu\dot \phi\dot \rho/J$，所以 $\frac{ \,\mathrm{d}{u} }{ \,\mathrm{d}{\phi} }=\dot u/\dot \phi=\mu\dot \rho/J$。式 7 式就可以改写为 $u$ 与 $\phi$ 的方程：

\begin{equation} \begin{aligned} &\frac{J^2}{2\mu} \left(\frac{ \,\mathrm{d}{u} }{ \,\mathrm{d}{\phi} } \right) ^2=E-V(1/u)-\frac{J^2}{2\mu} u^2~,\\ & \left(\frac{ \,\mathrm{d}{u} }{ \,\mathrm{d}{\phi} } \right) ^2=\frac{2\mu}{J^2} \left(E-V(1/u) \right) )-u^2~. \end{aligned} \end{equation}

或将上式两侧对 $\phi$ 求导，得到二阶运动方程：

\begin{equation} \begin{aligned} \frac{{ \,\mathrm{d}{}} ^2 u}{ \,\mathrm{d}{\phi} ^2}\frac{ \,\mathrm{d}{u} }{ \,\mathrm{d}{\phi} }+\frac{ \,\mathrm{d}{u} }{ \,\mathrm{d}{\phi} }u&=\frac{\mu}{J^2}\frac{- \,\mathrm{d}{V} \left(1/u \right) }{ \,\mathrm{d}\left(1/u \right) }\frac{ \,\mathrm{d}\left(1/u \right) }{ \,\mathrm{d}{u} }\frac{ \,\mathrm{d}{u} }{ \,\mathrm{d}{\phi} } \\ \Rightarrow \frac{{ \,\mathrm{d}{}} ^2 u}{ \,\mathrm{d}{\phi} ^2}+u&=-\frac{\mu}{J^2u^2}F(1/u)~. \end{aligned} \end{equation}

式 8 式 9 被称为比耐公式（Binet 公式）。关于中心力场运动问题的比耐公式的推导，还可以参考。

2. 开普勒问题

　　在开普勒问题中，相互作用势为 $V(\rho)=-Gm_1m_2/\rho=-k/\rho$。那么式 8 变为

\begin{equation} \begin{aligned} \left|\frac{ \,\mathrm{d}{u} }{ \,\mathrm{d}{\phi} }\right|&=\sqrt{-u^2+\frac{2\mu k}{J^2}u+\frac{2\mu E}{J^2}}\\ &=\sqrt{- \left(u-\frac{\mu k}{J^2} \right) ^2+\frac{2\mu E}{J^2}+\frac{\mu^2 k^2}{J^4}}~. \end{aligned} \end{equation}

该一阶偏微分方程的解的形式为

\begin{equation} u-\frac{\mu k}{J^2}=\alpha \cos\left(\phi-\beta\right) ~, \end{equation}

可以解得

\begin{equation} \begin{aligned} \alpha=\sqrt{\frac{2\mu E}{J^2}+\frac{\mu^2 k^2}{J^4}}~.\\ \end{aligned} \end{equation}

这样就求得了 $u$ 关于 $\phi$ 的表达式。最后将 $u$ 用 $\rho=1/u$ 表示，得到

\begin{equation} \rho=\frac{p}{1+e \cos\left(\phi-\beta\right) }~, \end{equation}

其中 $e$ 为轨道的偏心率（或者称离心率）。$p,e$ 由下式给出：

\begin{equation} \begin{aligned} &p=\frac{J^2}{\mu k}\\ &e=\frac{J^2}{\mu k}\alpha=\sqrt{1+\frac{2J^2E}{\mu k^2}}~, \end{aligned} \end{equation}

　　开普勒问题的轨道运动方程还可以用龙格—楞次矢量求解。

3. 卢瑟福散射问题

　　卢瑟福通过用 $\alpha$ 粒子轰击金箔，否定了汤姆孙的葡萄干面包模型。卢瑟福惊讶地发现，每 20000 个粒子中，有 1 个 $\alpha$ 粒子会被反弹回去，这是汤姆孙的理论无法解释的。根据卢瑟福的设想，原子内部应该有一个体积很小的区域聚集了所有的正电荷，而负电荷则围绕着它在转，这使得 $\alpha$ 粒子轰击金箔这个两体问题的相互作用可以近似为库仑相互作用。卢瑟福因此提出原子的行星轨道模型，为原子结构的研究作出巨大贡献，于 1908 年获得诺贝尔化学奖。

　　在卢瑟福散射问题中，设粒子 1 质量 $m_1$，带电荷 $q_1$；粒子 2 质量 $m_2$，带电荷 $q_2$。两个粒子都是带正电荷的粒子，那么它们之间就有排斥力，相互作用势为

\begin{equation} V(\rho)=\frac{q_1q_2}{4\pi\epsilon_0\rho}=-\frac{k}{\rho}~. \end{equation}

相互作用势与 $\rho$ 成反比，因此还可以用求解开普勒问题的方法计算。不同的是这里 $k$ 为负数，因此

\begin{equation} \begin{aligned} &p=-\frac{J^2}{\mu |k|}\\ &e=-\sqrt{1+\frac{2J^2E}{\mu k^2}}~, \end{aligned} \end{equation}

\begin{equation} \rho=\frac{p}{1+e \cos\left(\phi-\beta\right) }=\frac{J^2/\mu |k|}{\sqrt{1+2J^2E/\mu k^2} \cos\left(\phi-\beta\right) -1}~. \end{equation}

为使分母 $>0$，$\phi$ 有一定取值范围：

\begin{equation} \cos\left(\phi-\beta\right) >\frac{1}{|e|} \Rightarrow \phi \in (\phi_1,\phi_2)~. \end{equation}

粒子从无穷远飞来，到与另一粒子距离极小时开始返回，再飞回无穷远。轨道的形状为双曲线。散射角（粒子的偏转角度）$\theta$ 满足为

\begin{equation} \cot\frac{\theta}{2}=\tan\frac{|\phi_1-\phi_2|}{2} =\sqrt{e^2-1}=\sqrt{\frac{2J^2E}{\mu k^2}}~. \end{equation}

　　（在随粒子 1 平动的参考系中）设粒子 2 从无穷远的距离以 $ \boldsymbol{\mathbf{v}} _0$ 的速度靠近粒子 1，开始运动所在直线与粒子 2 的距离为 $b$（称为碰撞距离），那么角动量为 $J=\mu bv_0$，能量为 $E=\mu v_0^2/2$。因此可以得到散射角 $\theta$ 与 $b,v_0$ 的关系式：

\begin{equation} \cot \frac{\theta}{2}=\frac{\mu bv_0^2}{k}~. \end{equation}

如果发射大量相同速度粒子 2，探测被粒子 1 “弹” 回的各个方向上的粒子数——不同的碰撞距离将导致不同的散射角。微分散射截面的信息往往反应粒子间相互作用的信息，以帮助人们对粒子的内部结构进行猜测，或对已有的猜想进行实验验证。根据微分散射截面的定义（散射），$ \,\mathrm{d}{\Omega} =2\pi \sin\theta \,\mathrm{d}{\theta} $，$ \,\mathrm{d}{\sigma} =2\pi b \,\mathrm{d}{b} $，有

\begin{equation} \frac{ \,\mathrm{d}{\sigma} }{ \,\mathrm{d}{\Omega} }=\frac{b}{\sin \theta}\left|\frac{ \,\mathrm{d}{b} }{ \,\mathrm{d}{\theta} }\right|~. \end{equation}

对式 20 两边微分，得到 $ \,\mathrm{d}{b} $ 和 $ \,\mathrm{d}{\theta} $ 的关系：

\begin{equation} -\frac{ \,\mathrm{d}{\theta} /2}{\sin^2(\theta/2)}=\mu v_0^2 \,\mathrm{d}{b} /k\Rightarrow \left|\frac{ \,\mathrm{d}{b} }{ \,\mathrm{d}{\theta} }\right|=\frac{|k|}{2\mu v_0^2\sin^2(\theta/2)}~, \end{equation}

那么

\begin{equation} \begin{aligned} \frac{ \,\mathrm{d}{\sigma} }{ \,\mathrm{d}{\Omega} }&=\frac{ \cot\left(\theta/2\right) |k|/(\mu v_0^2)}{\sin\theta}\cdot \frac{|k|}{2\mu v_0^2\sin^2(\theta/2)}=\frac{k^2}{4\mu ^2v_0^4\sin^4(\theta/2)} \\ &=\frac{k^2}{16E^2\sin^4(\theta/2)}~, \end{aligned} \end{equation}

其中 $k=-k_eq_1q_2=-q_1q_2/(4\pi\epsilon_0)$（这里 $k_e$ 是静电常数）。该公式与式 4 是一致的。