贡献者: addis
预备知识 1 波包的延迟(量子力学)
,库仑函数
,选择定则
,含时微扰理论
本文使用原子单位制。例如一个有限深势阱(短程势)中有一个束缚态,被一个电场波包电离之后,光电子波包逃出势阱。那么光电子波包的延迟是多少呢?我们以下使用一阶含时微扰理论来分析。
1. 一维势阱的光电离延迟
我们假设势阱在坐标原点,且 $t = 0$ 时电场波包的中心刚好到达原点。
初态和末态能量分别为 $E_0, E$,令 $\omega = E - E_0$,不含时的末态记为 $\psi_k(x)$,并令其为满足边界条件
\begin{equation}
\psi_k(x \to +\infty) = \frac{1}{\sqrt{2\pi}} \mathrm{e} ^{ \mathrm{i} kx}~,
\end{equation}
其中 $A(k)$ 是实函数。那么一阶微扰系数为(
式 11 )
\begin{equation}
c(k) = - \mathrm{i} \sqrt{2\pi} \left\langle \psi_k \middle| H' \middle| \psi_0 \right\rangle \tilde f(-\omega)~.
\end{equation}
电离波包可以由末态展开:
\begin{equation}
\psi(x, t) = \int_{-\infty}^{\infty} C(k) \psi_k(x) \mathrm{e} ^{- \mathrm{i} E t} \,\mathrm{d}{k} ~.
\end{equation}
那么根据
式 10 延迟为($k$ 视为 $E$ 的函数)
\begin{equation}
t = \frac{\partial}{\partial{E}} \arg C(k)~.
\end{equation}
对于没有 chirp 的电场波包,$\tilde f(-\omega)$ 相位恒定(实对称函数的傅里叶变换也是实对称的,乘以 $\sin$,$\cos$ 也只是左右平移一下)。所以随 $E$ 变化的相位只有矩阵元,绝对时间延迟为
\begin{equation}
t = \frac{\partial}{\partial{E}} \arg \left\langle \psi_k \middle| H' \middle| \psi_0 \right\rangle ~,
\end{equation}
这个延迟是相对与 $t = 0$ 也就是电磁波包到达原点的时间。
2. 氢原子的光电离延迟:库仑球面波基底
还是考虑类氢原子,库仑球面波(式 5 )记为 $ \left\lvert C_{l,m}(k) \right\rangle $,包含球谐函数 $Y_{l,m}( \hat{\boldsymbol{\mathbf{r}}} )$。含时微扰得($E = k^2/2$)
\begin{equation}
\left\lvert \psi(t) \right\rangle = \sum_{l,m} \int c_{l,m}(k) \left\lvert C_{l,m}(k) \right\rangle \mathrm{e} ^{- \mathrm{i} E t} \,\mathrm{d}{k} ~,
\end{equation}
其中系数为
\begin{equation}
c_{l,m}(k) = -\sqrt{2\pi} \mathrm{i} \left\langle C_{l,m}(k) \middle| z \middle| i \right\rangle \tilde f(-\omega)~.
\end{equation}
\begin{equation}
\frac{\partial}{\partial{E}} \arg c_{l,m} = \frac{\partial}{\partial{E}} \arg \left\langle C_{l,m}(k) \middle| z \middle| i \right\rangle = 0~.
\end{equation}
注意对于氢原子束缚态作为初始态,由于选择定则 $\Delta m = 0$,$\Delta l = \pm 1$(只有这时 $ \left\langle C_{l,m}(k) \middle| z \middle| i \right\rangle $ 不为零),只有最多两个 $c_{l,m}$ 不为零。如果从基态电离就只有 $c_{1,0} = 1$(线偏振光)。
既然系数相位不随能量变化,那么延迟从哪来呢?从基底!
库仑渐进形式为(式 8 )
\begin{equation}
F_l(k, r) \overset{r\to \infty}{\longrightarrow} \sin \left[kr - \frac{\pi l}{2} + \frac{Z}{k} \ln\left(2kr\right) + \sigma_l(k) \right] ~, \end{equation}
库仑相移为
\begin{equation}
\sigma_l(k) = \arg[\Gamma(l+1- \mathrm{i} Z/k)] = \operatorname{Im} \ln\Gamma(l+1- \mathrm{i} Z/k) \qquad (Z > 0)~.
\end{equation}
图 1:库仑相移 $\sigma_l(k)$
但这也是一个实函数,怎么办?可以把它看成向内和和向外的行波叠加!各形成一个波包,叠加以后初始波包也是实函数,但向左的消失了,向右的出现了,所以一小段时间后就会出现一个向右的波包,完全由向右的行波贡献。所以可以直接把 $\sin$ 看成 $\frac{1}{2 \mathrm{i} } \mathrm{e} ^{ \mathrm{i} kx + \dots}$。现在就和一维散射情况一样了,但注意径向波函数需要考虑离心势能 $l(l+1)/(2mr^2)$。这也是为什么经典轨迹模拟中不能用直线而是用具有角动量的双曲线。这个离心势能,对应的就是氢原子的 $t_\text{EWS}^\text{H}$!
\begin{equation}
t_\text{EWS}^l = \frac{\partial}{\partial{E}} \arg \left\langle C_{l,m}(k) \middle| \psi(t) \right\rangle = \frac{\partial \sigma_l}{\partial E} ~.
\end{equation}
根据
图 1 它恒大于零,随能量单调递减。
但是式 6 中库仑球面波本身还存在关于 $r$ 不收敛的相移 $-\eta \ln\left(2kr\right) $,这对能量求导以后对足够大的 $r$ 会得到小于零的延迟,即提前。从经典物理的角度来看,提前是因为一开始电子在势阱中移动的速度比无穷远处更快,节约了一些时间。重申,对于氢原子基态的线性光电离,只需要 $l = 1$,结果与方向无关。所以氢原子 streaking 电离的角向变化完全是由 $t_\text{CLC}$ 决定的。
所以
\begin{equation}
\begin{aligned}
t_\text{EWS}^l &= \frac{1}{k} \operatorname{Im} \frac{\mathrm{d}}{\mathrm{d}{k}} \ln\Gamma(l+1- \mathrm{i} Z/k) = \frac{1}{k} \operatorname{Im} \frac{ \frac{\mathrm{d}}{\mathrm{d}{k}} \Gamma(l+1- \mathrm{i} Z/k)}{\Gamma(l+1- \mathrm{i} Z/k)}\\
&= \frac{Z}{k^3} \operatorname{Re} \frac{\Gamma'(l+1- \mathrm{i} Z/k)}{\Gamma(l+1- \mathrm{i} Z/k)}~.
\end{aligned}
\end{equation}
另外 $\Gamma'(x)/\Gamma(x)$ 被称为
双 $\Gamma$ 函数。
其中 $\sigma_l(k)$ 产生的相移与距离无关,可以单纯看作是非直线轨道带来的延迟(不确定),并且是 XUV 波包一瞬间带来的。$kr \ln\left(2kr\right) $ 只和距离有关,带来的延迟是库仑力产生的,而且关于 $r$ 并不收敛。那么光电离的总延迟就是
\begin{equation}
t_\text{XUV} = t_\text{EWS}^l + t_\text{C} = \frac{\partial}{\partial{E}} \sigma_l(k) + \frac{\partial}{\partial{E}} \frac{Z}{k} \ln\left(2kr\right) ~. \end{equation}
第一项是瞬间的,而第二项是波包移动过程中缓慢积累且不收敛的:
\begin{equation}
t_\text{C}(k, r) = \frac{Z}{k^3}[1- \ln\left(2kr\right) ]~.
\end{equation}
一定要强调光电离延迟 $\tau$ 和 streaking 延迟是不一样的。在 Streaking 实验中,前两项都会直接转换为 streaking 延迟(因为电离瞬间产生)。第三项在上式中不收敛,但 streaking 延迟却总是收敛的。配合 IR 的扰动就变为了 $t_\text{CLC}$ 项。
=============== 回收 ================
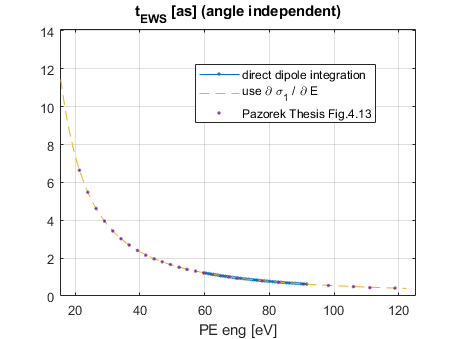
根据 Pazourek 的延迟理论,对氢原子,总的 streaking 延迟为
\begin{equation}
t_s = t_{EWS} + t_{CLC}~.
\end{equation}
其中 $t_s$ 直接通过 streaking 谱得到。$t_{EWS}$ 可以通过 XUV-only 的波包来测量,或者等效地用
transition dipole来计算。
令 $ \boldsymbol{\mathbf{\mathcal E}} $ 为电场常矢量,$C_{ \boldsymbol{\mathbf{k}} }$ 为库仑平面波,$ \left\lvert 0 \right\rangle $ 为基态,则
\begin{equation}
t_{EWS} = \frac{\partial}{\partial{E}} \arg \left\langle C_{ \boldsymbol{\mathbf{k}} } \middle| \boldsymbol{\mathbf{\mathcal E}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} \middle| 0 \right\rangle = \frac{\partial}{\partial{E}} \arg \left\langle C_{ \boldsymbol{\mathbf{k}} } \middle| \hat{\boldsymbol{\mathbf{k}}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} \middle| 0 \right\rangle ~.
\end{equation}
由于基态的对称性,完全可以假设 $ \hat{\boldsymbol{\mathbf{k}}} = \hat{\boldsymbol{\mathbf{z}}} $,所以这个结果是和角度无关的。
现在可以进一步把式 16 中的 $ \left\lvert C_{ \boldsymbol{\mathbf{k}} } \right\rangle $ 展开为分波。根据选择定则,只有 $l = 1$ 的分波有贡献。最后得
\begin{equation}
t_{EWS} = \frac{\partial}{\partial{E}} \arg \left\langle C_{ \boldsymbol{\mathbf{k}} } \middle| \boldsymbol{\mathbf{\mathcal E}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} \middle| 0 \right\rangle = \frac{\partial \sigma_l}{\partial E} ~.
\end{equation}
局部延迟
那么如果波包不是在无穷远而是在某个不太远的 $r$ 处,又当如何应对?这是参考的直线轨迹到底是取当前位置的,还是无穷远处的?还是都不行?我们不妨把 $1/r$ 势能在变化足够缓慢的时候近似为一些阶梯。每个阶梯内都是
\begin{equation}
\exp\left[ \mathrm{i} k_i x + \sigma_l(k) + (Z/k) \ln 2kr_i\right] \qquad (k_i^2 - Z/r_i = k^2)~.
\end{equation}
($r_i$ 在每个阶梯内是常数)。那么结论是显然的,如果只保留波包
\begin{equation}
\int A(k) \exp\left( \mathrm{i} k_i x\right) \,\mathrm{d}{k} = \int \frac{k_i}{k}A(k) \exp\left( \mathrm{i} k_i x\right) \,\mathrm{d}{k_i} ~,
\end{equation}
把 $A(k_i)$ 的中心变为了 $k_i$,还出现小小的扭曲(假设可以忽略),但总体来说,现在 $A(k_i)$ 具有以当前阶梯势能为准的中心动量,所以波包轨迹是以该局部动量为斜率的直线。而加上两个相位后,延迟也是相对这条直线而言的,而不是相对于末动量的直线。
3. 氢原子的光电离延迟:库仑平面波基底
对于氢原子,一阶微扰也可以直接投影到库仑平面波(式 2 ,取减号)$ \left\lvert C( \boldsymbol{\mathbf{k}} ) \right\rangle $($E = k^2/2$)
\begin{equation}
\left\lvert \psi(t_f) \right\rangle = \int c( \boldsymbol{\mathbf{k}} ) \left\lvert C( \boldsymbol{\mathbf{k}} ) \right\rangle \mathrm{e} ^{- \mathrm{i} E t} \,\mathrm{d}^{3}{k} ~,
\end{equation}
\begin{equation}
c( \boldsymbol{\mathbf{k}} ) = -\sqrt{2\pi} \mathrm{i} \left\langle C( \boldsymbol{\mathbf{k}} ) \middle| z \middle| i \right\rangle \tilde f(-\omega)~.
\end{equation}
这相对于
式 6 不过是变换了一下基底。其中库仑平面波为
\begin{equation}
\left\lvert C( \boldsymbol{\mathbf{k}} ) \right\rangle = \sum_{l,m} a_{l,m}^{(-)}( \boldsymbol{\mathbf{k}} ) \left\lvert C_{l,m} \right\rangle ~,
\end{equation}
把 $ \left\lvert \psi(t) \right\rangle $ 投影到 $ \left\lvert C( \boldsymbol{\mathbf{k}} ) \right\rangle $ 上有(
式 12 )
\begin{equation}
\left\langle C( \boldsymbol{\mathbf{k}} ) \middle| \psi(t) \right\rangle = \sum_{l,m} a_{l,m}^{(-)*}( \boldsymbol{\mathbf{k}} ) c_{l,m}(k) \mathrm{e} ^{- \mathrm{i} E t}
= \sum_{l,m} \frac{ \mathrm{i} ^{-l}}{k} \mathrm{e} ^{ \mathrm{i} \sigma_l} Y_{l,m} ( \hat{\boldsymbol{\mathbf{k}}} ) c_{l,m}(k) \mathrm{e} ^{- \mathrm{i} E t}~.
\end{equation}
求和中每一项可以看作一个独立的波包,具有不同的延迟。所以和
式 4 同理,每一项的延迟仅由库仑相移贡献($ \left\langle C_{l,m}(k) \middle| z \middle| i \right\rangle $ 是实数,$c_{l,m}(k)$ 不贡献相位变化)
\begin{equation}
t_\text{EWS}^l = \frac{\partial}{\partial{E}} \arg \left\langle C( \boldsymbol{\mathbf{k}} ) \middle| \psi(t) \right\rangle = \frac{\partial \sigma_l}{\partial E} ~.
\end{equation}
可见使用平面波和球面波计算延迟是一样的。
根据边界条件式 1 ,$ \left\lvert C( \boldsymbol{\mathbf{k}} ) \right\rangle $ 的无穷远平面波是不含库仑相移的(已经在系数中抵消掉了),但自带一个不收敛的相位 $-\eta \ln 2kr$,而电场的傅里叶变换 $\tilde f(-\omega)$ 相位恒定,所以对某个方向 $ \hat{\boldsymbol{\mathbf{k}}} $,有
\begin{equation}
t_\text{XUV} = \frac{\partial}{\partial{E}} \arg \left[ \left\langle C( \boldsymbol{\mathbf{k}} ) \middle| z \middle| i \right\rangle + \frac{Z}{k} \ln\left(2kr\right) \right] ~.
\end{equation}
这和
式 13 只是使用的基底不同,所以是等价的。
4. 经典力学直线轨迹延迟
如果考虑光电子的经典力学直线轨迹,那么它的延迟是多少呢?注意直线轨迹虽然简单,但氢原子单光子电离以后只有 $l=1$,角动量不为零。所以用径向直线的经典轨迹(角动量为零)来类比是不太准确的。正确的做法应该是使用双曲线轨道([PazoTh]),暂时不考虑。
\begin{equation} \begin{aligned}
\int \frac{1}{\sqrt{2(k^2/2+Z/r)}} \,\mathrm{d}{r} &= \frac{r}{k}\alpha-\frac{2 Z}{k^3}\tanh ^{-1}\alpha + C\\
&=F(r)+ C'~.
\end{aligned} \end{equation}
其中
\begin{equation}
\alpha = \sqrt{\frac{2 Z}{k^2 r}+1},
\quad C' = C + \mathrm{i} \pi/2~,
\end{equation}
\begin{equation}
F(r) = \frac{r}{k}\alpha-\frac{Z}{k^3} \ln\left(\frac{\alpha+1}{\alpha-1}\right) ~,
\end{equation}
这是因为(
式 7 )
\begin{equation}
\tanh ^{-1} x
= \frac12 \ln\left(\frac{x+1}{x-1}\right) + \mathrm{i} \frac{\pi}{2} \qquad (x > 1)~.
\end{equation}
令 $C'$ 前面的部分为 $F(x)$,那么当粒子从 $r=a$ 运动到 $r=b$,比起 $k$ 速直线运动的时间,多了
\begin{equation}
\Delta t_\text{XUV}^{cl} = \left. \left[F(x)-\frac{r}{k} \right] \right\rvert _{r=a}^{r=b} < 0~.
\end{equation}
\begin{equation} \begin{aligned}
\lim_{r\to \infty} \left[F(x)-\frac{r}{k} \right] =
\frac{Z}{k^3} \left[1- \ln\left(2k r\right) -\ln\frac{k}{Z} \right] ~.
\end{aligned} \end{equation}
\begin{equation} \begin{aligned}
\lim_{r\to 0} \left[F(x)-\frac{r}{k} \right] =
\frac{\sqrt{2Zr}}{k^2} \to 0~.
\end{aligned} \end{equation}
所以,当一个粒子从 $r\to 0$ 出发,到一个很大的距离,当对于匀速直线运动,产生的延迟就是
\begin{equation}
t_\text{XUV}^{cl} = \left. \left[F(x)-\frac{r}{k} \right] \right\rvert _{r\to0}^{r\to\infty} = \frac{Z}{k^3} \left[1- \ln\left(2kr\right) -\ln\frac{k}{Z} \right] ~.
\end{equation}
这与
式 14 只相差一个常数以及库仑相位对能量偏导。
在该模型中,可以认为
\begin{equation}
t_\text{EWS}^{cl} = t_\text{XUV}^{cl} - t_C = -\frac{Z}{k^3}\ln\frac{k}{Z}~.
\end{equation}
库仑相位的来源是径向方程中的 $l(l+1)/(2mr^2)$ 项,我们在直线轨迹中并没有考虑! 如果使用双曲线轨道,经典力学也会有这一项。
如果使用式 1 ,那么可以得到离心率
\begin{equation}
e = \sqrt{1 + l(l+1)k^2/Z^2}~.
\end{equation}
以及
\begin{equation}
\tan\left(\theta/2\right) = b/a = \frac{k}{Z}\sqrt{l(l+1)} = \frac{kL}{Z}~.
\end{equation}
也就是说双曲线的偏转角为 $35.6^\circ$ 左右,还是不小的(数值模拟中为什么没有发现?)。
5. 氦原子
氦原子的延迟完全也可以分别使用子节 2 和子节 3 两种方法。这是完全一样的。一阶微扰的末态必须是能量本征态,氦原子和 $H$ 对易的算符只有 $L^2, L_z$,所以精确的球面波能量本征态记为 $ \left\lvert E,L,M \right\rangle $。它可以分解为
\begin{equation}
\left\lvert E,L,M \right\rangle = \frac{1}{r_1r_2}\sum_{l_1,l_2}\psi_{l_1,l_2}^{L, M}(r_1, r_2)\mathcal Y_{l_1,l_2}^{L, M}( \hat{\boldsymbol{\mathbf{r}}} _1, \hat{\boldsymbol{\mathbf{r}}} _2)~.
\end{equation}
理论上要解本征态 $ \left\lvert E,L,M \right\rangle $,就用许多无限长的长方形网格,每张网格是一个 $(l_1,l_2,L)$ 分波,网格之间被 $1/r_{12}$ 势能耦合。网格上 $r_1$ 在区间 $(0,a]$,$r_1 = a$ 处边界条件是波函数为 “零”,另外两条边 $r_1 = r_2 = 0$ 也有波函数为零。$r_2$ 的区间为 $(0,\infty)$,这样才能保证 $E$ 可以连续取值而不是离散的。由于边界条件和耦合项都是实函数,解出的 $\psi_{l_1,l_2}^{L, M}(r_1, r_2)$ 也必是实函数。
但波函数有 6 维度,我们只确定了三个量子数 $H,L,M$,所以还可以规定在 $r_2\to\infty$ 时,某个 $(l_1,l_2)$ 分波是束缚态和库仑波函数($Z=1$)的乘积,其他分波无穷远处都为零
\begin{equation}
\begin{aligned}
&\psi_{l'_1,l'_2}^{L, M}(r_1, r_2) \overset{r_2\to\infty}{\longrightarrow} \delta_{l_1,l'_1}\delta_{l_2,l'_2} r_1 R_{n_1,l_1}^{(Z=2)}(r_1)
\sin \left[k_2 r_2 - \frac{\pi l_2}{2} +\frac{1}{k_2} \ln\left(2k_2 r_2\right) + \sigma_{l_2} + \delta_{n_1,l_1,l_2}^{L,M} \right] ~.
\end{aligned}
\end{equation}
最后一项就是库仑函数 $F_{l_2}(k_2 r_2 + \delta_{n_1,l_1,l_2}^{L,M})$ 的渐进形式。这样就可以把这个态记为 $ \left\lvert n_1,L,M,l_1,l_2,k_2 \right\rangle $。在 Pazourek 的论文中提到一个 R-matrix 方法可以解出这样的波函数
1。这个态仍然只有 $E,L,M$ 是 well defined。如果把这些态用 CG 系数线性组合一下,就可以得到
\begin{equation}
\begin{aligned}
& \left\lvert n_1,l_1,m_1,l_2,m_2,k_2 \right\rangle
= 2 \mathrm{i} \sum_{L} \begin{bmatrix}l_1& l_2& L\\ m_1& m_2& M\end{bmatrix} \mathrm{e} ^{- \mathrm{i} \delta_{n_1,l_1,l_2}^{L,M}} \left\lvert n_1,L,M,l_1,l_2,k_2 \right\rangle ~,
\end{aligned}
\end{equation}
渐进形式为:
\begin{equation}
\left\lvert n_1,l_1,m_1, l_2,m_2,k_2 \right\rangle \overset{r_2\to\infty}{\longrightarrow} r_1 R_{n_1,l_1}(r_1) F_{l_2}(r_2 + \delta_{l_2})~.
\end{equation}
注意此时除了能量,里面的量子数都只是在 $r_2\to+\infty$ 处是 well defined。
微扰理论中的矩阵元可以用(注意对称化)$ \left\langle n_1,l_1,m_1, l_2,m_2,k_2 \middle| z_1 + z_2 \middle| i \right\rangle $,这同样是实数,剩下的论述就和氢原子的一样了。要获得平面波出射的散射态,就做线性组合
\begin{equation}
\left\lvert n_1, l_1, m_1, \boldsymbol{\mathbf{k}} _2 \right\rangle = \sum_{l_2,m_2}\frac{ \mathrm{i} ^{l_2}}{k_2} \mathrm{e} ^{- \mathrm{i} (\sigma_{l_2}+\delta_{l_2})} Y_{l_2,m_2} ( \hat{\boldsymbol{\mathbf{k}}} _2) \left\lvert n_1,l_1,m_1, l_2,m_2,k_2 \right\rangle ~,
\end{equation}
这个态中同样只包含一个库仑 $-\eta\ln 2kr$ 相位。把一阶微扰的末态投影到上面后,光电离的总延迟就是
\begin{equation}
t = \frac{\partial}{\partial{E}} \arg \left[\delta_{l_2} + \sigma_{l_2} + \frac{Z}{k_2} \ln\left(2k_2 r_2\right) \right] ~, \end{equation}
比起氢原子多了一项 $\delta_{l_2}$。事实上如果给氢原子加上一个 SAE 势能同样也会多出这样一个相位。
和上文氢原子同理,也可以直接以 $ \left\lvert n_1, l_1, m_1, \boldsymbol{\mathbf{k}} _2 \right\rangle $ 作为基底计算一阶微扰,结果相同:
\begin{equation}
\frac{\partial}{\partial{E}} \arg \left\langle n_1, l_1, m_1, \boldsymbol{\mathbf{k}} _2 \middle| z_1 + z_2 \middle| i \right\rangle = \frac{\partial}{\partial{E}} (\delta_{l_2} + \sigma_{l_2})~.
\end{equation}
选择定则
但氦原子的本征态是 $L,M$ 算符的本征态,而且从基态的一阶微扰是 $L = 1, M = 0$。所以根据三角形法则(图 2 ),可以支持 $ \left\lvert l_2 - l_1 \right\rvert \le 1$ 除了 $(0,0)$ 的所有分波。
1. ^ Philip G. Burke, R-Matrix Theory of Atomic Collisions - Application to Atomic, Molecular and Optical Processes, Springer