贡献者: addis; 欄、停敘
预备知识 椭圆,抛物线
,
双曲线,右手定则
,平面旋转矩阵
椭圆的存在如此普遍,以至于早在在公元前 3 世纪的古希腊时期,在没有坐标、没有代数、没有计算器的情况下,数学家阿波罗尼奥斯(Apollonius of Perga)就在《圆锥曲线论》中对它进行了研究。
阿波罗尼奥斯之前的古人相信天体运行是完美的圆。但随着时间推移,人们观察到了不那么完美的现象:行星轨迹有 “逆行”,日月运行有周期波动,日月食不是完全等间距出现等等。这些 “不完美” 让人开始思考:也许圆不是唯一的完美曲线。在这样的气氛下,阿波罗尼奥斯提出圆锥曲线是一种比圆更丰富的几何家族,是一种可能的 “自然运动路径”。
阿波罗尼乌斯受欧几里得《几何原本》的影响,希望将所有圆锥曲线系统化,像欧几里得那样构建一个逻辑完备的 “曲线几何宇宙”。
1. 圆锥视角下的圆锥曲线
圆锥曲线之所以叫做圆锥曲线,是因为它们可以由平面截取圆锥面得到(图 1 )。然而由于这涉及较为繁琐的计算,所以初学圆锥曲线时我们往往先介绍更简单的定义,例如 “圆锥曲线的极坐标方程” 中的定义,或者直接在 $x$-$y$ 直角坐标系中使用二次方程定义(见预备知识)。以下我们来证明双圆锥被平面截出的任意曲线都是圆锥曲线。
图 1:圆锥的有限截面是一个椭圆(来自 Wikipedia)
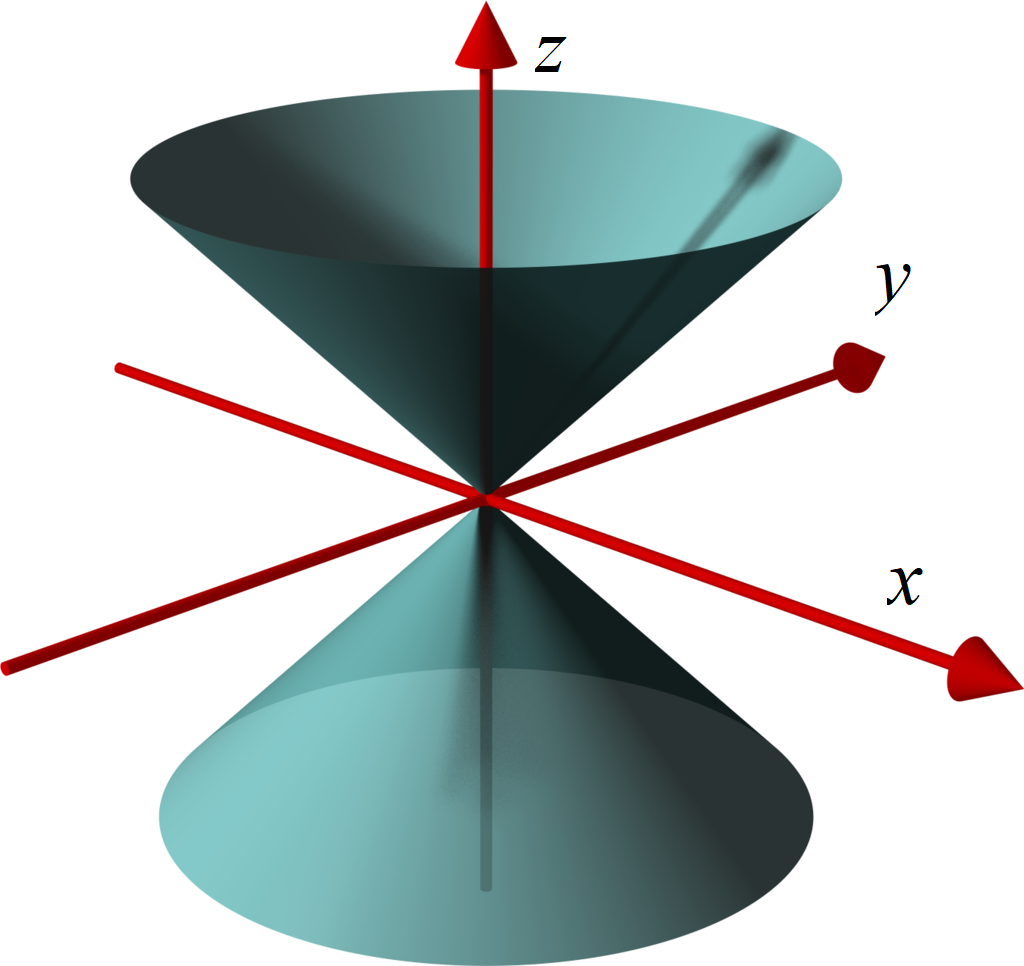
双圆锥面如图 2 所示。在直角坐标系 $x$-$y$-$z$ 中,为了方便我们使用顶角(两条母线的最大夹角)为 $\pi/2$ 的圆锥
图 2:
式 1 表示的双圆锥面(修改自 Wikipedia)
其方程为
\begin{equation}
z_1^2 = x_1^2 + y_1^2~.
\end{equation}
对其他顶角的圆锥,我们只需要把 $z$ 轴缩放一下即可。
我们可以再列出一个一般的平面方程与式 1 联立得到方程组,但这样解出来的曲线将与 $x$-$y$ 平面未必平行。所以更方便的办法是先把圆锥旋转一下,再用某个和 $x$-$y$ 平面平行的平面 $z = z_0$ 去截出曲线。这样就方便化为圆锥曲线的标准方程。关于 $y$ 轴的旋转变换为1
\begin{equation}
\begin{pmatrix}x_1\\z_1\end{pmatrix} = \begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{pmatrix} \begin{pmatrix}x\\z\end{pmatrix} ~,
\end{equation}
\begin{equation}
y_1 = y~.
\end{equation}
代入
式 1 得
\begin{equation}
(\sin\theta\cdot x + \cos\theta\cdot z)^2 = (\cos\theta\cdot x - \sin\theta\cdot z)^2 + y^2~.
\end{equation}
这相当于把圆锥关于 $y$ 轴用
右手定则旋转了 $\theta$。当 $\theta \ne \pi/4$ 时,化成椭圆或双曲线的标准方程(
式 16 式 18 )
\begin{equation}
\frac{(x - \tan2\theta \cdot z)^2}{(z/\cos2\theta)^2} + \frac{y^2}{z^2/\cos2\theta} = 1~.
\end{equation}
长半轴、短半轴和离心率分别为
\begin{equation}
a = \frac{z}{\cos2\theta}~,
\qquad
b = \frac{z}{\sqrt{ \left\lvert \cos2\theta \right\rvert }}~,
\qquad
e = \sqrt{2}\sin\theta~.
\end{equation}
当 $\theta < \pi/4$ 时,式中 $\cos2\theta > 0$,就得到了椭圆($e < 1$),反之则得到双曲线。
当 $\theta = \pi/4$,式 4 化为抛物线($e = 1$)的标准方程(式 22 )
\begin{equation}
y^2 = 2zx~.
\end{equation}
1. ^ 式 2 和式 3 可以表示为 $3\times 3$ 的三维旋转矩阵。