贡献者: half-tree; addis
- 本文处于草稿阶段。
- 本文缺少预备知识,初学者可能会遇到困难。
类比平面旋转矩阵,空间旋转矩阵是三维直角坐标的旋转变换,所以应该是 $3 \boldsymbol\times 3$ 的方阵。不同的是平面旋转变换只有一个自由度 $\theta $,而空间旋转变换除了转过的角度还需要考虑转轴的方向,三维空间中的方向有两个自由度,所有三维旋转矩阵共有 3 个自由度。
若已经知道空间直角坐标系中三个单位正交矢量
\begin{equation}
\hat{\boldsymbol{\mathbf{x}}} = \begin{pmatrix}1\\0\\0\end{pmatrix} ~, \quad
\hat{\boldsymbol{\mathbf{y}}} = \begin{pmatrix}0\\1\\0\end{pmatrix} ~, \quad
\hat{\boldsymbol{\mathbf{z}}} = \begin{pmatrix}0\\0\\1\end{pmatrix} ~.
\end{equation}
经过三维旋转矩阵变换以后变为另外三个正交归一矢量。仍然以 $ \hat{\boldsymbol{\mathbf{x}}} , \hat{\boldsymbol{\mathbf{y}}} , \hat{\boldsymbol{\mathbf{z}}} $ 作为基底,把他们分别记为
\begin{equation}
\begin{pmatrix}a_{11}\\a_{21}\\a_{31}\end{pmatrix} ~,\quad \begin{pmatrix}a_{12}\\a_{22}\\a_{32}\end{pmatrix} ~,\quad \begin{pmatrix}a_{13}\\a_{23}\\a_{33}\end{pmatrix} ~.
\end{equation}
类比
平面旋转矩阵,可以得到旋转矩阵为
\begin{equation}
\boldsymbol{\mathbf{R}} _3 = \begin{pmatrix}
{a_{11}}&{a_{12}}&{a_{13}}\\
{a_{21}}&{a_{22}}&{a_{23}}\\
{a_{31}}&{a_{32}}&{a_{33}}
\end{pmatrix}~.\end{equation}
这 9 个矩阵元只有 3 个是独立的,因为我们有 6 个条件:每个列矢量模长等于 1(3 个等式),且两两间正交(3 个等式)。
除了通过三个单位矢量构建旋转矩阵,我们可以通过由转轴的方向和旋转的角度来计算每个矩阵元,参考 “罗德里格旋转公式” 和 “四元数”。另一种常见的方法是使用欧拉角。
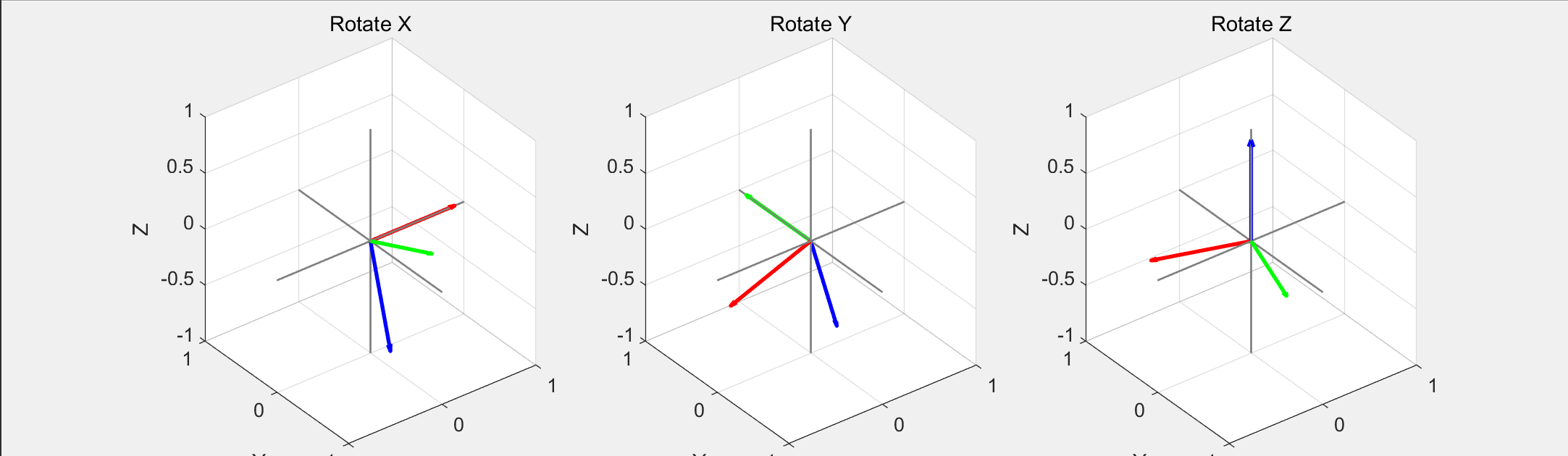
例 1 分别给出绕 $x,y,z$ 轴旋转的三维矩阵。
图 1:旋转矩阵
出于转轴已经固定为某一条坐标轴,所以仅需要一个参量 $\theta$ 就可以确定旋转后的矩阵状态。
以绕 $x$ 轴旋转的三维矩阵为例,由上图可以发现,基底 $ \hat{\boldsymbol{\mathbf{x}}} $ 在转轴上,不做变换;而 $ \hat{\boldsymbol{\mathbf{y}}} $ 与 $ \hat{\boldsymbol{\mathbf{z}}} $ 垂直于转轴,故其方向发生变化。
设由 $y$ 轴正方向向 $z$ 轴负方向转动为正向转动,转动角为 $\theta$,我们可以知道,原基底 $ \hat{\boldsymbol{\mathbf{y}}} = \begin{pmatrix}0\\1\\0\end{pmatrix} $ 将转变为 $ \hat{\boldsymbol{\mathbf{y}}} '= \begin{pmatrix}0\\ \cos{\theta} \\ -\sin{\theta}\end{pmatrix} $。同理,原基底 $ \hat{\boldsymbol{\mathbf{z}}} = \begin{pmatrix}0\\0\\1\end{pmatrix} $ 将在转动中转变为 $ \hat{\boldsymbol{\mathbf{z}}} '= \begin{pmatrix}0\\ \sin{\theta} \\ \cos{\theta}\end{pmatrix} $。
综上所述,结合转换后的基底结果,我们知道描述以 $y$ 轴正方向向 $z$ 轴负方向转动为正向转动,绕 $x$ 轴旋转的三维矩阵可以表示为
\begin{equation}
\boldsymbol{\mathbf{M}} _x = \begin{pmatrix}
1 & 0 & 0 \\
0 & \cos{\theta} & -\sin{\theta} \\
0 & \sin{\theta} & \cos{\theta}
\end{pmatrix}~.\end{equation}
同样的,绕 $y$ 轴或者绕 $z$ 轴旋转的矩阵也可以用类似的办法推出,我们也可以得到相应的矩阵为
\begin{equation}
\boldsymbol{\mathbf{M}} _y = \begin{pmatrix}
\cos{\theta} & 0 & \sin{\theta} \\
0 & 1 & 0 \\
-\sin{\theta} & 0 & \cos{\theta}
\end{pmatrix}~.\end{equation}
\begin{equation}
\boldsymbol{\mathbf{M}} _z = \begin{pmatrix}
\cos{\theta} & -\sin{\theta} & 0 \\
\sin{\theta} & \cos{\theta} & 0 \\
0 & 0 & 1
\end{pmatrix}~.\end{equation}
1. 被动理解
结合 平面旋转矩阵 中关于二维的旋转矩阵的知识,我们可以发现对二维平面做旋转相当于对当前的基做 式 1 的矩阵变换。
现在,让我们观察二维旋转矩阵的表达式
\begin{equation}
\begin{pmatrix}x'\\ y'\end{pmatrix} =
\begin{pmatrix}
\cos\theta & - \sin\theta\\
\sin\theta &\cos\theta
\end{pmatrix} \begin{pmatrix}x\\ y\end{pmatrix} ~.
\end{equation}
对于矩阵的行空间,定义 $u_{x}= \begin{pmatrix}\cos{\theta} \\ -\sin{\theta}\end{pmatrix} ^{\top} ,\quad u_{y}= \begin{pmatrix}\sin{\theta} \\ \cos{\theta}\end{pmatrix} ^{\top}.$
则我们可以发现变换后的新基底实际上是旋转矩阵的行空间向量与原基底的内积,如下所示
\begin{equation}
x' = u_{x} \cdot \begin{pmatrix}x\\ y\end{pmatrix} ~;
\end{equation}
\begin{equation}
y' = u_{y} \cdot \begin{pmatrix}x\\ y\end{pmatrix} ~.
\end{equation}
相应地,这个规律可以推广到更高维度的情况,对于一个三维的旋转矩阵而言,变换后的新基底仍然是旋转矩阵的行空间向量与原基底的内积,以 式 3 为例,对于 $ \begin{pmatrix}x' \\ y' \\ z'\end{pmatrix} = \boldsymbol{\mathbf{R}} _3 \cdot \begin{pmatrix}x \\ y \\ z\end{pmatrix} $,有以下表达式成立
\begin{equation}
x' = u_{x} \cdot \begin{pmatrix}x \\ y \\ z\end{pmatrix} ~; \quad
y' = u_{y} \cdot \begin{pmatrix}x \\ y \\ z\end{pmatrix} ~; \quad
z' = u_{z} \cdot \begin{pmatrix}x \\ y \\ z\end{pmatrix} ~.
\end{equation}
其中,$u_{x} = \begin{pmatrix}a_{11} \\ a_{12} \\ a_{13}\end{pmatrix} ^{\top}, \quad u_{y} = \begin{pmatrix}a_{21} \\ a_{22} \\ a_{23}\end{pmatrix} ^{\top}, \quad u_{z} = \begin{pmatrix}a_{31} \\ a_{32} \\ a_{33}\end{pmatrix} ^{\top}.$
所以说,像这样的变换,可以用矩阵向量空间和原向量的内积来表示。进而我们想到:任何直角坐标的变换都可以用内积来完成。这也就是矩阵乘法定义的另一种解释。
2. 逆矩阵
定理 1 列向量都是单位向量,且任意两向量正交的矩阵是正交矩阵
证明如下:
对于一个正交矩阵 $ \boldsymbol{\mathbf{P}} $ 来说,有 $ \boldsymbol{\mathbf{P}} ^{-1} = \boldsymbol{\mathbf{P}} ^{\top} $ 成立,这也就等价于 $ \boldsymbol{\mathbf{P}} ^{\top} \cdot \boldsymbol{\mathbf{P}} = \boldsymbol{\mathbf{I}} $ 成立。
为了证明该定理,我们设 $ \boldsymbol{\mathbf{P}} = \begin{pmatrix}p_{1}, p_{2} ... p_{n}\end{pmatrix} $,其中 $p_{i}$ 是 $ \boldsymbol{\mathbf{P}} $ 的列向量,满足 $\forall i \ne j$,有 $p_{i} \cdot p_{j} = 0$,同时 $\forall i = j$,有 $p_{i} \cdot p_{j} = 1$。
我们也可以知道其逆矩阵 $ \boldsymbol{\mathbf{P}} ^{\top} = \begin{pmatrix}p_{1}^{\top} \\ p_{2}^{\top} \\ ... \\ p_{n}^{\top}\end{pmatrix} $。
为了计算 $ \boldsymbol{\mathbf{P}} ^{\top} \cdot \boldsymbol{\mathbf{P}} $,考虑我们在上文提到的矩阵乘法等同于内积的思想,该乘法所得到的矩阵元应当是 $ \boldsymbol{\mathbf{P}} ^{\top}$ 中对应行向量与 $ \boldsymbol{\mathbf{P}} $ 中对应列向量内积的值,有下方表达式成立
\begin{equation}
\boldsymbol{\mathbf{P}} ^{\top} \cdot \boldsymbol{\mathbf{P}} = \begin{pmatrix}
p_{1}^{\top} \cdot p_{1} & p_{1}^{\top} \cdot p_{2} & ... & p_{1}^{\top} \cdot p_{n} \\
p_{2}^{\top} \cdot p_{1} & p_{2}^{\top} \cdot p_{2} & ... & p_{2}^{\top} \cdot p_{n} \\
... & ... & & ...\\
p_{n}^{\top} \cdot p_{1} & p_{n}^{\top} \cdot p_{2} & ... & p_{n}^{\top} \cdot p_{n}
\end{pmatrix}~.\end{equation}
根据矩阵 $ \boldsymbol{\mathbf{P}} $ 向量的性质,有且仅有对角线上的元素(满足 $i = j$)为 $1$,其余位置的元素(有 $i \ne j$)皆为 $0$。可以推得 $ \boldsymbol{\mathbf{P}} ^{\top} \cdot \boldsymbol{\mathbf{P}} =
\begin{pmatrix}
1 & 0 & ... & 0 \\
0 & 1 & ... & 0 \\
... & ... & & ...\\
0 & 0 & ... & 1\end{pmatrix} = \boldsymbol{\mathbf{I}} $
综上所述,列向量都是单位向量,且向量之间两两正交的矩阵是正交矩阵。
习题 1 根据上面的证明过程,解释为什么如果所有列矢量正交归一,所有行矢量也会正交归一。
注:正交归一指的是一组向量不仅两两正交,而且每个向量都是单位向量。
提示:$ \boldsymbol{\mathbf{P}} $ 的列向量和 $ \boldsymbol{\mathbf{P}} ^{\top}$ 的行向量是一致的。
我们可以知道,对于平面或三维的旋转矩阵,其表示的基向量应当是单位向量,且两两之间应当也是正交的。这是因为表示旋转操作的矩阵并不会拉伸空间,且其仍然保持原基底的夹角不发生变化。
所以,旋转矩阵实际上也是正交矩阵,根据正交矩阵的定义,我们有 $ \boldsymbol{\mathbf{P}} ^{\top} = \boldsymbol{\mathbf{P}} ^{-1}$,旋转矩阵的逆与它的转置一致。