贡献者: addis; _Eden_
回顾:函数是一个非空集合 $A$ 到另一个集合 $B$ 的对应法则。
本文中,函数 $f$ 是指从 $\mathbb R$ 的某个非空子集 $X$ 到 $\mathbb{R}$ 的映射
1. 函数的极限
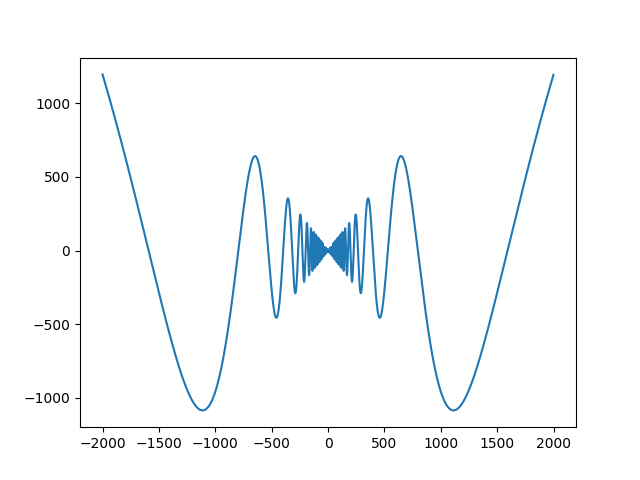
图 1:请添加图片描述
定义 1 邻域和去心邻域
定义邻域为:$U(x_0,\delta)=\{x\in \mathbb{R}:|x-x_0|<\delta\}$.
定义去心邻域为:$U_0(x_0,\delta)= U(x_0,\delta) \backslash \{x_0\}=\{x\in \mathbb{R}:0<|x-x_0|<\delta\}$.
定义 2 极限
设函数 $f(x)$ 在 $U_0(x_0,\delta_0)$($\delta_0>0$)内有定义。
若存在实数 $A$,使得对任意 $\epsilon >0$,存在 $\delta>0$,使得当 $x\in U_0(x_0,\delta)$ 时,有 $|f(x)-A|<\epsilon$,则称当 $x$ 趋于 $x_0$,函数 $f(x)$ 以 $A$ 为极限,记为 $\large \lim\limits_{x\rightarrow x_0}f(x)=A$ 或 $f(x)\rightarrow A\ (x\rightarrow x_0)$。
补充:实际上有更宽泛的定义,只要 $x_0$ 是函数 $f(x)$ 定义域的聚点,就可以定义在该点处的极限。
同序列极限的性质类似,函数极限也具有唯一性:
定理 1
若函数 $f(x)$ 在 $x_0$ 处极限存在,证明在 $x_0$ 处极限唯一。
习题 1
- $f(x)=\left\{\begin{aligned} 0\ \ &(x<1)\\ 1\ \ &(x\ge 1) \end{aligned}\right.$,判断 $f(x)$ 在 $x_0=1$ 处极限是否存在。
- $f(x)=\left\{\begin{aligned} 0\ \ &(x<1)\\ 1\ \ &(x= 1)\\2\ \ &(x>1) \end{aligned}\right.$,判断 $f(x)$ 在 $x_0=1$ 处极限是否存在。
- $f(x)=x\cdot \sin\left(1/x\right) $,判断 $f(x)$ 在 $x_0=0$ 处极限是否存在。
- $f(x)= \sin\left(1/x\right) $,判断 $f(x)$ 在 $x_0=0$ 处极限是否存在。
- $f(x)= \mathrm{e} ^x$,证明 $\lim\limits_{x\rightarrow a}= \mathrm{e} ^a,\forall a\in\mathbb{R}$。
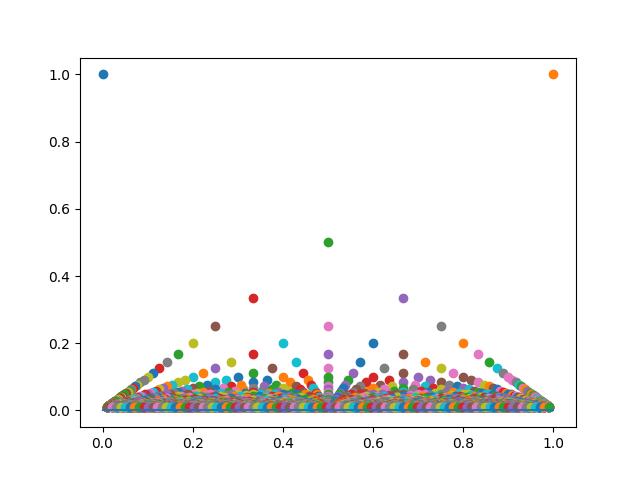
图 2:黎曼函数
我们来看一个有趣的函数 $f(x)$,它的定义域为 $[0,1]$:
\begin{equation}
f(x)=\left\{
\begin{aligned}
&1/q && (x=\frac{p}{q}\ (p,q\in \mathbb{N},\frac{p}{q}\text{为既约真分数}))\\
&0 && (\text{x=0 或 x=1 或 x}\notin \mathbb{Q})~.
\end{aligned}
\right.
\end{equation}
我们称它为
黎曼(Riemann)函数。
虽然在定义域内有无穷多个点的函数值不为 $0$,但 $f(x)$ 的极限却处处为 $0$,我们之后还将看到,$f(x)$ 在无理点处处连续,但 $f(x)$ 处处不可导。
习题 2
- 证明:若函数 $f(x)$ 在 $U(a,\delta_0)(\delta_0>0)$ 上有定义,且满足 $\large\lim\limits_{x\rightarrow a}f(x)=f(a)$,那么对任意极限为 $a$ 的序列 $\{x_n\}$,序列 $\{f(x_n)\}$ 的极限也为 $f(a)$。
上述命题反过来也成立。
- 对于任意给定的序列 $\{a_n\}(0< a_n<1)$,构造定义域为 $[0,1]$ 的函数 $f(x)$,满足 $\forall x\in \{a_n\},f(x)\neq 0;\ \forall x \in [0,1]\backslash \{a_n\},f(x)=0$,且 $f(x)$ 在定义域上极限处处为 $0$。
2. 函数的左右极限
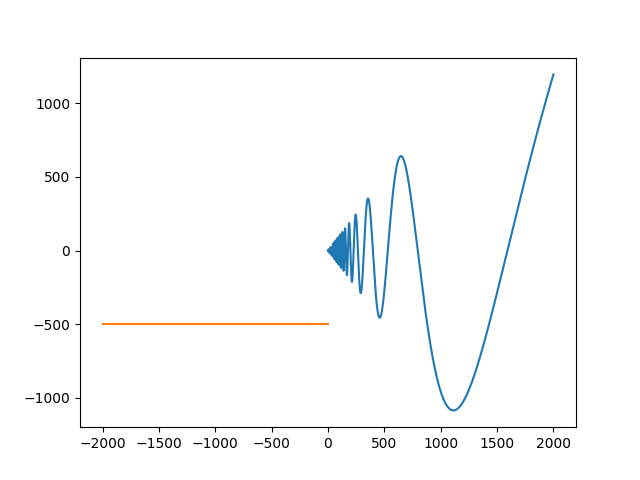
图 3:请添加图片描述
如果把去心邻域 $U_0(x_0,\delta_0)$ 分成两块单侧邻域——
左空心邻域:$U_0^+(x_0,\delta)=U_0(x_0,\delta)\cap (x_0,+\infty) \{x\in \mathbb{R} :x_0< x< x_0+\delta\}~.$
右空心邻域:$U_0^-(x_0,\delta)=U_0(x_0,\delta)\cap (-\infty,x_0) \{x\in \mathbb{R} :x_0-\delta< x< x_0\}~.$
那么就可以定义函数的左右极限:
设 $f(x)$ 在 $U^+_0(x_0,\delta_0)(\delta_0>0)$ 上有定义。
如果存在实数 $A$,使得对任意 $\epsilon >0$,存在 $\delta>0$,当 $x\in U_0^+(x_0,\delta)$ 时,有 $|f(x)-A|<\epsilon$,则称 $f(x)$ 在点 $x_0$ 的右极限存在,而称 $A$ 为 $f(x)$ 在点 $x_0$ 的右极限,记为 $\lim\limits_{x\rightarrow x_0^+}f(x)=A$ 或 $f(x_0^+)=A$。
类似地可以定义左极限存在和左极限。
习题 3
- $f(x)=\left\{\begin{aligned} 0\ \ &(x<1)\\ 1\ \ &(x= 1)\\2\ \ &(x>1) \end{aligned}\right.$,判断 $f(x)$ 在 $x_0=1$ 处的左极限与右极限。
- $f(x)=[x]$(取整函数),判断 $f(x)$ 在 $x_0=1$ 处的左极限与右极限。
- 设函数 $f(x)$ 在 $U_0(x_0,\delta_0)$ 上有定义,证明:$\lim\limits_{x\rightarrow x_0} f(x)=A$ 当且仅当 $\lim\limits_{x\rightarrow x_0^-}f(x)=\lim\limits_{x\rightarrow x_0^+}f(x)=A$。
3. 函数极限的各种情况
称集合 $\{x:|x|>h\}(h>0)$ 为 $\infty$ 的邻域,记为 $U(\infty,h)$(这时就没有必要定义去心邻域了)。
同样的可以分成两块单侧邻域:
\begin{equation}
\begin{aligned}
&U^+(\infty,h)=U(\infty,h)\cup (0,\infty)=\{x:x>h\}~,\\
&U^-(\infty,h)=U(\infty,h)\cup (-\infty,0)=\{x:x<-h\}~.
\end{aligned}
\end{equation}
这样就可以函数在自变量趋向于无穷大时的极限:
设函数 $f(x)$ 在 $U^+(\infty,h_0)$ 上有定义。若存在实数 $A$,使得 $\forall \epsilon >0, \exists X\in U^+(\infty,h_0)$,当 $x>X$ 时,有 $|f(x)-A|<\epsilon$,则称当 $x$ 趋于 $+\infty$ 时 $f(x)$ 的极限存在,其极限为 $A$,记为 $\lim\limits_{x\rightarrow +\infty}f(x)=A$ 或 $f(x)\rightarrow A(x\rightarrow +\infty)$。
类似地可以定义 $\lim\limits_{x\rightarrow -\infty}f(x)=A$ 和 $\lim\limits_{x\rightarrow \infty}f(x)=A$。
习题 4
- 设函数 $f(x)$ 在 $U(\infty,h_0)$ 上有定义,证明:$\lim\limits_{x\rightarrow \infty} f(x)=A$ 当且仅当 $\lim\limits_{x\rightarrow -\infty}f(x)=\lim\limits_{x\rightarrow +\infty}f(x)=A$。
- 设序列 $\{a_n\}$ 收敛于 $A$,定义函数 $f(x)=a_{|[x]+1|}$,证明:$\lim\limits_{x\rightarrow \infty} f(x)=A$。
定义 3 广义极限
如果自变量趋向于一个值时,函数趋向于无穷大,则可以定义广义极限:
设 $f(x)$ 在 $U_0(x_0,\delta_0)(\delta_0>0)$ 上有定义,若 $\forall M>0,\exists \delta>0$,使得当 $x\in U_0(x,\delta)$ 时,有 $f(x)>M$,则称当 $x$ 趋于 $x_0$,$f(x)$ 趋于 $+\infty$,或称当 $x$ 趋于 $x_0$ 时,$f(x)$ 的广义极限为 $+\infty$。记为 $\lim\limits_{x\rightarrow x_0}f(x)=+\infty$ 或 $f(x)\rightarrow +\infty(x\rightarrow x_0)$。此时也称 $f(x)$ 为当 $x$ 趋于 $x_0$ 时的正无穷大量。
同样地可以定义负无穷大量和无穷大量。
对于函数极限而言,自变量有以下几种变化情况:
\begin{equation}
x\rightarrow x_0;\ x\rightarrow x_0^+;\ x\rightarrow x_0^{-};\ x\rightarrow \infty;\ x\rightarrow +\infty;\ x\rightarrow -\infty~.
\end{equation}
对于这六种情况可以定义各自的
广义极限:
\begin{equation}
f(x)\rightarrow A;\ f(x)\rightarrow +\infty;\ f(x)\rightarrow -\infty;\ f(x)\rightarrow \infty~,
\end{equation}
因此一共有 $24$ 种可能的函数极限的情形。
但由于它们之间有极大的相似之处,所以很容易进行记忆和想象。
习题 5
- $f(x)=x^2\sin x$,判断它是不是当 $x\rightarrow \infty$ 时的无穷大量。
- $f(x)=1/(x-1)\ (x\neq 1)$,求 $f(1^-),f(1^+),\lim\limits_{x\rightarrow 1}f(x),\lim\limits_{x\rightarrow \infty}f(x)$。
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。