贡献者: 小熊慢慢说; addis
1. 电场做功
如果空间中存在某种分布的静电场(关于位置的矢量函数)$ \boldsymbol{\mathbf{E}} ( \boldsymbol{\mathbf{r}} )$,一个电荷为 $q$ 的点电荷在任意位置 $ \boldsymbol{\mathbf{r}} $ 都会受到电场力
\begin{equation}
\boldsymbol{\mathbf{F}} ( \boldsymbol{\mathbf{r}} ) = q \boldsymbol{\mathbf{E}} ( \boldsymbol{\mathbf{r}} )~.
\end{equation}
这样我们就得到了一个由电场力构成的力场,与电场处处成正比。
从某点 $ \boldsymbol{\mathbf{r}} _1$ 沿着某个路径移动到另一点 $ \boldsymbol{\mathbf{r}} _2$,电场对它做功为(式 4 )
\begin{equation}
W = \int_{ \boldsymbol{\mathbf{r}} _1}^{ \boldsymbol{\mathbf{r}} _2} \boldsymbol{\mathbf{F}} ( \boldsymbol{\mathbf{r}} ) \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } = q \int_{ \boldsymbol{\mathbf{r}} _1}^{ \boldsymbol{\mathbf{r}} _2} \boldsymbol{\mathbf{E}} ( \boldsymbol{\mathbf{r}} ) \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } ~.
\end{equation}
势能与保守场
要讨论势能或者电势的概念,我们首先需要确保力场 $ \boldsymbol{\mathbf{F}} ( \boldsymbol{\mathbf{r}} )$ 或电场 $ \boldsymbol{\mathbf{E}} ( \boldsymbol{\mathbf{r}} )$ 是一个保守场,即只有上式的结果只与初末位置有关而与路径无关时才可能存在一个势能函数。以后我们会看到电场可以分为两类:由电荷直接产生的电场是无旋的,即保守场,而由变化磁场产生的电场是有旋的,即非保守场(见 “力场 势能”,“斯托克斯定理”)。
这个问题有两种解决方法,第一是要求净电荷分布不随时间变化,且电流保持恒定1,这类问题称为静电学(electrostatics)。在静电学问题中,空间中没有变化的磁场,所以所有的电场都是由净电荷产生的无旋场,总可以定义电势。
第二种方法是,在非静电学的情况下,我们将电场中的保守场部分分离出来定义电势(能),即在式 2 的积分中,$ \boldsymbol{\mathbf{E}} ( \boldsymbol{\mathbf{r}} )$ 并不取总电场,而是取其中的无旋部分2。例如电路中的电压(电势差)就是通过这种方法定义的。因为一般来说电路不满足静电学的条件,例如电路中的线圈可能存在电磁感应。
2. 电势能
记电势能(electric potential energy)函数(关于位置的实函数)为 $E_p( \boldsymbol{\mathbf{r}} )$,就有 “力场对物体做功等于势能减少”,或者 “势能增加等于力场做的负功” 即
\begin{equation}
E_p( \boldsymbol{\mathbf{r}} _2) - E_p( \boldsymbol{\mathbf{r}} _1) = -W = -q \int_{ \boldsymbol{\mathbf{r}} _1}^{ \boldsymbol{\mathbf{r}} _2} \boldsymbol{\mathbf{E}} ( \boldsymbol{\mathbf{r}} ) \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } ~.
\end{equation}
根据上式,我们只能判断两点之间的势能差,若要完全确定势能函数,还需要指定零势点的位置 $ \boldsymbol{\mathbf{r}} _0$(可以取无穷远)使得 $E_p( \boldsymbol{\mathbf{r}} _0) = 0$(类比万有引力势能)。于是任意一点的势能为
\begin{equation}
E_p( \boldsymbol{\mathbf{r}} ) = -q \int_{ \boldsymbol{\mathbf{r}} _0}^{ \boldsymbol{\mathbf{r}} } \boldsymbol{\mathbf{E}} ( \boldsymbol{\mathbf{r}} ') \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} ~.
\end{equation}
微分关系为
\begin{equation}
\boldsymbol{\mathbf{F}} = q \boldsymbol{\mathbf{E}} ( \boldsymbol{\mathbf{r}} ) = - \boldsymbol\nabla E_p~.
\end{equation}
例 1 匀强电场
假设空间中存在匀强电场 $ \boldsymbol{\mathbf{E}} = E_x \hat{\boldsymbol{\mathbf{x}}} + E_y \hat{\boldsymbol{\mathbf{y}}} + E_z \hat{\boldsymbol{\mathbf{z}}} $,即电场矢量与位置无关。以原点为零势点 $ \boldsymbol{\mathbf{r}} _0$,求点电荷 $q$ 在空间中任意一点 $ \boldsymbol{\mathbf{r}} $ 的电势能。
根据式 4 ,取积分路径为原点到 $ \boldsymbol{\mathbf{r}} $ 的线段,则
\begin{equation}
E_p( \boldsymbol{\mathbf{r}} ) = -q \boldsymbol{\mathbf{E}} \int_{ \boldsymbol{\mathbf{0}} }^{ \boldsymbol{\mathbf{r}} } \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} = -q \boldsymbol{\mathbf{E}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} ~.
\end{equation}
当 $ \boldsymbol{\mathbf{r}} $ 和 $ \boldsymbol{\mathbf{E}} $ 同方向时,就得到了高中所学的 $-qEr$。
3. 电势
注意以上公式中,无论是做功还是势能都与电荷量 $q$ 有关(成正比)。为了更直接地描述电场本身的性质,我们可以把这些公式两边都除以 $q$。若定义电势 $V( \boldsymbol{\mathbf{r}} )$ 满足
\begin{equation}
E_p( \boldsymbol{\mathbf{r}} ) = q V( \boldsymbol{\mathbf{r}} )~,
\end{equation}
则
式 3 和
式 4 就变为
\begin{equation}
V( \boldsymbol{\mathbf{r}} _2) - V( \boldsymbol{\mathbf{r}} _1) = - \int_{ \boldsymbol{\mathbf{r}} _1}^{ \boldsymbol{\mathbf{r}} _2} \boldsymbol{\mathbf{E}} ( \boldsymbol{\mathbf{r}} ) \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } ~.
\end{equation}
\begin{equation}
V( \boldsymbol{\mathbf{r}} ) = -\int_{ \boldsymbol{\mathbf{r}} _0}^{ \boldsymbol{\mathbf{r}} } \boldsymbol{\mathbf{E}} ( \boldsymbol{\mathbf{r}} ) \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } ~.
\end{equation}
同样,该积分只与初末位置有关而与路径无关。这样一来,电势就只是电场的属性而与电荷量无关了。微分关系为
\begin{equation}
\boldsymbol{\mathbf{E}} ( \boldsymbol{\mathbf{r}} ) = - \boldsymbol\nabla V( \boldsymbol{\mathbf{r}} )~,
\end{equation}
这相当于
式 5 两边除以 $q$。
4. 两个点电荷的电势
假设空间中有两个点电荷,$q_1$ 产生的电场可以根据式 2 计算,现在考虑 $q_2$ 在该场中的势能,取无穷远处为零势点,使用式 4 可以计算 $q_2$ 的势能为(这个过程可以类比万有引力势能的推导过程)
\begin{equation}
E_{p2} = -q_2 \int_{\infty}^{ \boldsymbol{\mathbf{r}} _1} \frac{1}{4\pi\epsilon_0} \frac{q_1}{r_{12}^3} \boldsymbol{\mathbf{r}} _{12} \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{r}} }
= \frac{1}{4\pi\epsilon_0} \frac{q_1 q_2}{r_{12}}~.
\end{equation}
有趣的是,计算 $q_1$ 在 $q_2$ 产生的电场中的势能结果也是一样的。事实上,电势能不储存于任何一个电荷中而是储存于电场中。以后我们会学习如何直接从总电场分布来计算势能,结果还是和上式一样。所以以后我们对这两种情况不加区分,都记为
\begin{equation}
E_p(r) = \frac{1}{4\pi\epsilon_0} \frac{q_1 q_2}{r_{12}}~.
\end{equation}
注意当两电荷异号时,$q_1 q_2$ 为负数,此时与万有引力一样,距离越近,势能越小。两电荷同号时 $q_1 q_2$ 为正,距离越远势能越小。
例 2
两个电荷量为 $Q$ 的电荷分别被固定在 $(-c, 0)$ 和 $(c, 0)$ 两点处,另一质量为 $m$ 电荷量为 $q$ 的点电荷从 $(0, a)$ 延直线移动到 $(0, b)$,试问它的动能增加了多少?
解:由式 12 可知,点电荷 $q$ 在 $(0, y)$ 处的电势能为
\begin{equation}
E_p = \frac{1}{4\pi\epsilon_0}\frac{2Qq}{\sqrt{y^2 + c^2}}~.
\end{equation}
所以动能增加等于势能减少,即
\begin{equation}
\Delta E_k = V_a - V_b = \frac{Qq}{2\pi\epsilon_0} \left(\frac{1}{\sqrt{a^2 + c^2}} - \frac{1}{\sqrt{b^2 + c^2}} \right) ~.
\end{equation}
5. 点电荷的电势能
由式 12 两边除以 $q_2$(或直接用式 9 )得 $ \boldsymbol{\mathbf{r}} _1$ 处单个点电荷在 $ \boldsymbol{\mathbf{r}} $ 处产生的电势为
\begin{equation}
V( \boldsymbol{\mathbf{r}} ) = \frac{1}{4\pi\epsilon_0} \frac{q}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} _1 \right\rvert }~.
\end{equation}
由于电场可以矢量叠加,易证电势和电势能也可以叠加
\begin{equation}
V( \boldsymbol{\mathbf{r}} ) = \frac{1}{4\pi\epsilon_0} \sum_i \frac{q_i}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} _i \right\rvert }~.
\end{equation}
6. 多个点电荷的电势能
当空间中存在 $N$ 个点电荷,取无穷远处电势为零,那么第 $i$ 个点电荷在剩下 $N-1$ 个点电荷产生的电场中的电势就是
\begin{equation}
V_i( \boldsymbol{\mathbf{r}} _i) = \frac{1}{4\pi\epsilon_0} \sum_j^{(j\ne i)} \frac{q_j}{ \left\lvert \boldsymbol{\mathbf{r}} _j - \boldsymbol{\mathbf{r}} _i \right\rvert }~,
\end{equation}
电势能为 $E_{pi}( \boldsymbol{\mathbf{r}} _i) = q_i V_i( \boldsymbol{\mathbf{r}} _i)$。这个能量的意义是:保持其他电荷位置不变,把点电荷 $q_i$ 从无穷远处移动到 $ \boldsymbol{\mathbf{r}} _i$ 处需要克服电场力所做的功。
如果要计算 $N$ 个电荷的总电势能,我们需要假设开始时这些点电荷两两间距离都是无穷远,然后把他们依次移动到 $ \boldsymbol{\mathbf{r}} _i$ 处所需要的总功:移动第 $q_1$ 个不需要做功,移动 $q_2$ 需要客服 $q_1$ 的电场力做功,移动第 $j$ 个电荷需要克服前 $j-1$ 个电荷的电场做功。所以
\begin{equation}
E_p = \frac{1}{4\pi\epsilon_0} \sum_{i,j}^{(i < j)} \frac{q_i q_j}{ \left\lvert \boldsymbol{\mathbf{r}} _j - \boldsymbol{\mathbf{r}} _i \right\rvert }~,
\end{equation}
其中小于号是为了在求和过程中不重复计算同一对电荷两次。如果不要求小于,则需要把结果除以 2
\begin{equation}
E_p = \frac{1}{8\pi\epsilon_0} \sum_{i, j}^{(j\neq i)} \frac{q_i q_j}{ \left\lvert \boldsymbol{\mathbf{r}} _j - \boldsymbol{\mathbf{r}} _i \right\rvert }~.
\end{equation}
将
式 17 代入该式得
\begin{equation}
E_p = \frac12 \sum_i q_i V_i( \boldsymbol{\mathbf{r}} _i)~,
\end{equation}
显然以上三种对电势能的定义是等效的。
7. 连续电荷分布的情况
将式 17 拓展到连续电荷分布的情况,令电荷密度分布为 $\rho( \boldsymbol{\mathbf{r}} )$,则某点的电势可以通过对整个空间体积分得到
\begin{equation}
V( \boldsymbol{\mathbf{r}} ) = \frac{1}{4\pi\epsilon_0} \int \frac{\rho( \boldsymbol{\mathbf{r}} )}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert } \,\mathrm{d}^{3}{r'} ~.
\end{equation}
例 3 求有限长细导体棒的电势分布
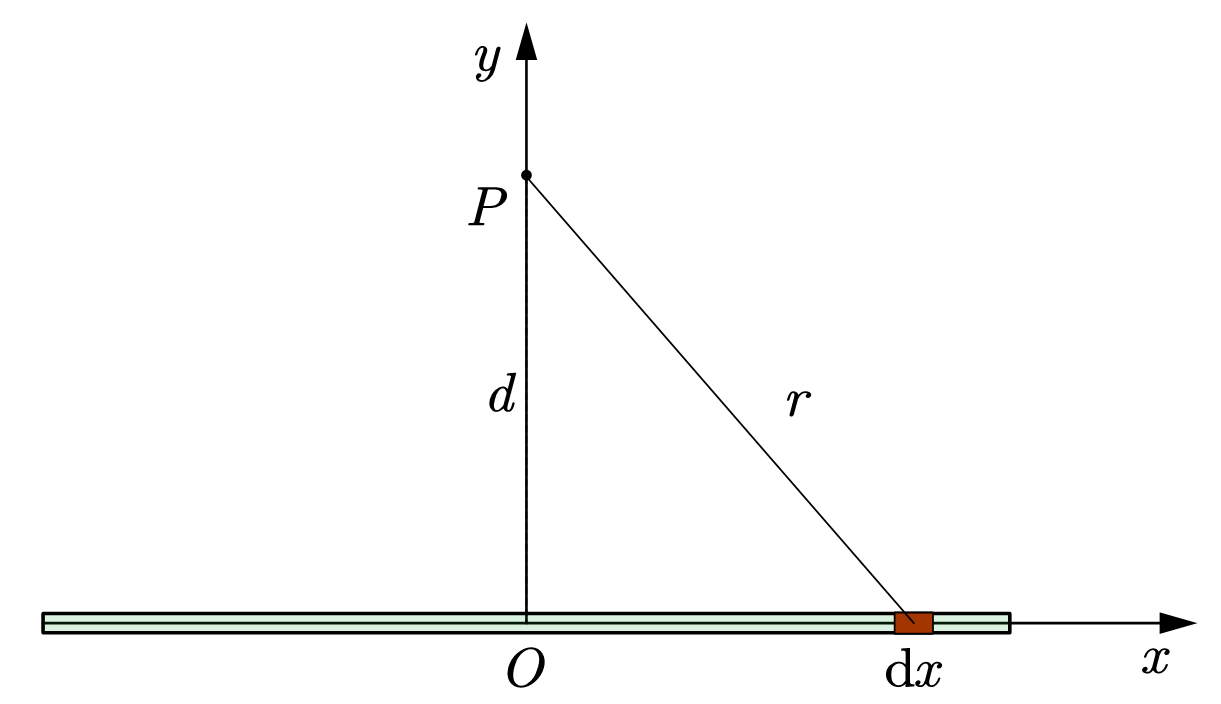
设带电直导线长为 $L$,线电荷密度为 $\lambda$。以导体棒中点为坐标原点,建立 $xOy$ 坐标系。现考虑导体棒的中垂线上与其距离为 $d$ 的 $P$ 点的电势。如下图所示。
图 1:有限长导体棒中轴线上的电势
对导线上的某一电荷微元,有 $ \,\mathrm{d}{q} =\lambda \,\mathrm{d}{x} $,该电荷微元到导线点 $P$ 的距离为 $r=\sqrt{x^2+d^2}$,该电荷微元对点 $P$ 贡献的电势为
\begin{equation}
\,\mathrm{d}{V} =\frac{1}{4\pi \epsilon_0}\frac{ \,\mathrm{d}{q} }{r}=\frac{1}{4\pi \epsilon_0}\frac{\lambda \,\mathrm{d}{x} }{\sqrt{x^2+d^2}}~.
\end{equation}
那么整段细导体棒对 $P$ 点的电势的贡献为
\begin{equation}
\begin{aligned}
V &=\frac{\lambda }{4 \pi \epsilon_{0}}\int_{-\frac{L}{2}}^{\frac{L}{2}}\frac{\mathrm{d} x}{\sqrt{x^{2}+d^{2}}}\\
&=\frac{\lambda }{4 \pi \epsilon_{0}}\ln_{}{(x+\sqrt{x^2+d^2})}\mid_{-\frac{L}{2}}^{\frac{L}{2}}\\
&=\frac{\lambda }{4 \pi \epsilon_{0}}\ln_{}{\frac{\sqrt{L^2+4d^2}+L}{\sqrt{L^2+4d^2}-L}}\\
&=\frac{\lambda }{4 \pi \epsilon_{0}}\ln_{}{ \left(\frac{\sqrt{L^2+4d^2}+L}{2d} \right) ^2}\\
&=\frac{\lambda }{2 \pi \epsilon_{0}}\ln_{}{\frac{\sqrt{L^2+4d^2}+L}{2d}}~.
\end{aligned}
\end{equation}
要注意的是,上述推导是以无穷远处为势能零点。若令棒长 $L\rightarrow \infty$,将得出任意位置的电势为无穷大的错误结论,此时以离无限长导体棒有限长度的位置为电势零点较为合适。
(未完成,使用式 21 ,对比例 1 的结论)
例 4 求均匀带电圆盘轴线上的电势
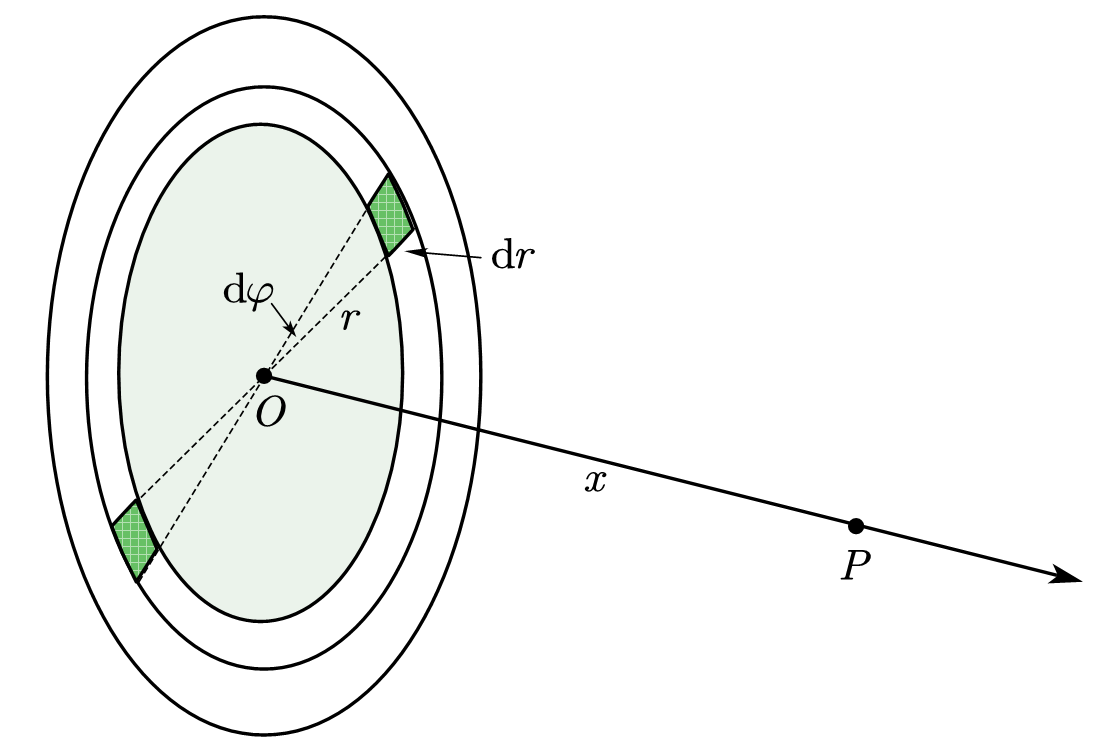
设圆盘半径为 $R$,圆盘的电荷面密度为 $\sigma$. 以圆盘中心为坐标原点,并在过原点且与圆盘垂直的方向上建立 $x$ 轴。令无穷远处为零势点。参考图如下
图 2:均匀带电圆盘轴线上的电势
用极坐标把圆盘平面分成许多面元,则坐标为 $r$、$\varphi$ 的面元的面积为 $ \,\mathrm{d}{S} =r \,\mathrm{d}{\varphi} \,\mathrm{d}{r} $,相应的电荷量为 $ \,\mathrm{d}{q} =\sigma \,\mathrm{d}{S} =\sigma r \,\mathrm{d}{\varphi} \,\mathrm{d}{r} $. 那么,该电荷微元对 $P$ 点的电势贡献为
\begin{equation}
\,\mathrm{d}{V} =\frac{1}{4 \pi \varepsilon_{0}}\frac{ \,\mathrm{d}{q} }{r}=\frac{\sigma}{4 \pi\varepsilon_{0} }\frac{r \,\mathrm{d}{\varphi} \,\mathrm{d}{r} }{ \sqrt{r^{2}+x^{2}}}~.
\end{equation}
对 $ \,\mathrm{d}{V} $ 积分,有
\begin{equation}
\begin{aligned}
V & =\frac{1}{4 \pi \varepsilon_{0}}\iint \frac{ \,\mathrm{d}{q} }{r}\\
& =\frac{\sigma }{4 \pi \varepsilon_{0}}\iint \frac{r \,\mathrm{d}{\varphi} \,\mathrm{d}{r} }{ \sqrt{r^{2}+x^{2}}}\\
& = \frac{\sigma}{4 \pi \varepsilon_{0}} \int_{0}^{2 \pi} \mathrm{d} \varphi \int_{0}^{R} \frac{r}{\sqrt{r^{2}+x^{2}}} \,\mathrm{d}{r} \\
& = \frac{\sigma}{2 \varepsilon_{0}}\left(\sqrt{R^{2}+x^{2}}-x\right)~.
\end{aligned}
\end{equation}
(未完成,使用式 21 ,对比例 2 的结论)
例 5 求均匀带电球内外的电势分布
设电荷面密度为 $\sigma$,令无穷远处为零势点
(未完成,使用式 21 ,对比例 2 的结论)
我们也可以类比式 20 ,写出连续电荷分布的电势能为
\begin{equation}
E_p = \frac 12 \int V( \boldsymbol{\mathbf{r}} ) \rho( \boldsymbol{\mathbf{r}} ) \,\mathrm{d}^{3}{r} ~.
\end{equation}
1. ^ 注意有电流就意味着有电荷在移动,所以我们强调的是 “净” 电荷保持静止
2. ^ 任何一个矢量场总可以分解成无散合无旋两部分,见 “亥姆霍兹分解”
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。