理想气体

贡献者： _Eden_

1. 理想气体与它的状态方程

　　 理想气体是真实气体在 $p\rightarrow 0,V\rightarrow \infty$ 的极限。它还有一种简要定义是：分子有质量无体积，分子间无作用的气体体系。理想气体的性质与物质无关，而且是一般气体体系的良好近似，所以是一个非常值得研究的重要的模型。

历史进程

　　 1787 年 Charles 提出查理定律，当气体体积固定时，气体温度 $T$ 和压强 $p$ 之间有确定的函数关系（$T$ 几乎和 $p$ 成正比）。1802 年，Gay-Lussac 提出盖·吕萨克定律，当气体压力保持不变时，气体温度和体积有确定的函数关系（温度几乎和体积成正比）。再后来，Boyle 提出波伊尔定律，若气体温度保持不变，压强和体积有确定的函数关系（几乎成反比）。我们可以总结得到：对于一个没有外力场的单元系统，处于热平衡时，其状态方程可写成 $f(T,p,V)=0$，也就是说只有两个独立参量。焦耳实验则表明，理想气体自由膨胀后温度不变，也就是说，理想气体内能只是温度的函数。下面让我们来具体看一下焦耳是怎么做的。

焦耳实验

　　 一个封闭的绝热的长方体容器，其中用隔板隔开，左侧是温度为 $T$ 的气体，右侧抽成真空。接着，我们将隔板抽出，左侧的气体便涌入右侧。最后，气体遍布整个长方体容器，我们再测量气体的温度，发现温度仍为 $T$（在实验中一定会存在一些误差）。如果我们承认能量守恒，在这个过程中气体前后内能没有发生变化，毕竟我们抽出隔板并没有做任何功，气体也没有从外界吸热，那么气体的内能¹应该不发生变化。那么焦耳实验则表明，对于同温度的理想气体，不管其体积如何变化，其内能都是恒定的。也就是说，一定量理想气体内能只是温度的函数，我们称之为焦耳定律。我们这里之所以说是理想气体，是因为实验表明焦耳定律在气体压强低、体积大的情况下更加准确，这种情况下气体更加接近于理想气体。

　　 在焦耳那个年代，人们并没有建立起气体的微观模型，焦耳的实验对热学的发展有巨大的推进作用。现在让我们回顾文章 “理想气体状态方程” 中对气体温度的微观解释，以及对内能的微观解释。当我们建立起理想气体的微观模型，对理想气体而言，单个气体分子的平均动能（由式 12 ）就是 $\frac{3}{2}PV/N = \frac{3}{2}k_B T$，气体分子总动能为 $\frac{3}{2}N k_B T=\frac{3}{2}nRT$，这就是气体的内能，从这个式子可以直观地看出一定量理想气体内能只是温度的函数。

理想气体状态方程及推广

　　 理想气体的状态方程为：$pV=nRT$，$R$ 为气体常数（$R\approx 8.3143\ \rm{J}(\rm{mol\cdot K})^{-1}$）；$n$ 为气体的摩尔数。

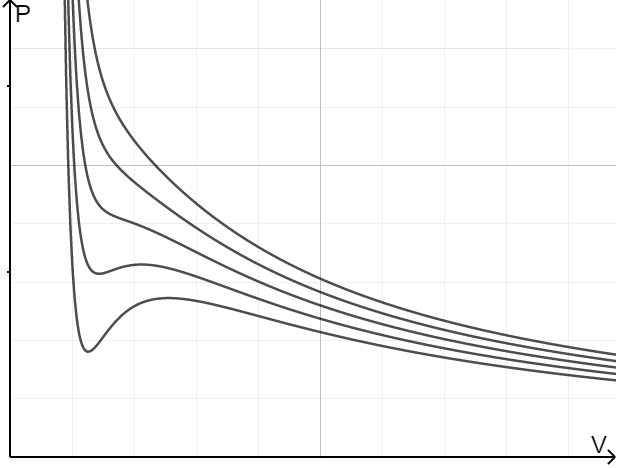
　　 范德瓦尔斯方程是理想气体向真实气体的推广，对理想气体作了两点修正：1、真实气体占据一定体积；2、真实气体间有分子间作用势（Lennard-Jones 势是一个很好的近似）。范德瓦尔斯方程展现出惊人的威力——从它的图像上可以看出气液相变线，可以找到临界点……1910 年诺贝尔物理学奖授予范德瓦尔斯，以表彰他为气体和液体状态方程所作的工作。

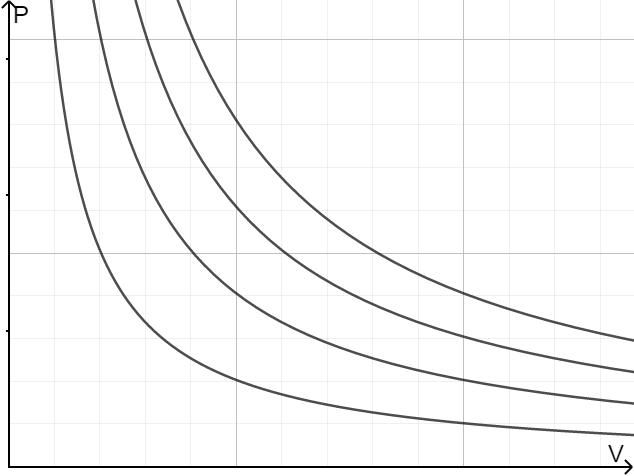
　　 从两者的等温线我们可以看出，理想气体的等温线是反比例函数。随着温度的升高，范德瓦尔斯气体的等温线越来越 “像” 反比例函数，即越来越接近理想气体。

2. 微观模型

　　 理想气体是研究热力学系统的一种模型。它的微观模型有几种基本假设：

1. 理想气体由大量运动的微观粒子组成。每个粒子都是质量为 $m$ 的质点，它的行为服从牛顿运动定律（注意，在标准状态下气体分子间平均距离和气体半径之比约为 $30$，所以可以近似地看作质点）。
2. 粒子间无相互作用（这意味着分子势能是刚球势）。粒子与粒子、粒子与容器之间发生碰撞，所有碰撞都是弹性碰撞。
3. 组成理想气体的粒子的运动是完全无序的、各向同性的²。完全无序体系无宏观运动。

　　 由以上三条基本假设，可以得到热力学中非常重要的细致平衡原理：达到平衡态的气体中能实现的任一正向的元过程，必定有一逆元过程与之相平衡。例如：在理想气体容器中的任意一个面元，每当有一个气体分子从左边穿过它到右边，就一定有另一个同样的分子在同一时刻从右边穿过面元来到左边。理想气体在现实的物理世界中是不可能存在的，但它作为一个理想化的模型可以简化大量计算，而且是一些气体系统的良好近似。

1. ^ 现在我们知道，气体的 “内能” 是所有气体分子的动能与势能之和；但在焦耳那个年代，热质说广为流行，人们并没有确立起气体的微观模型。
2. ^ 对于实际的气体分子，每时每刻都会与其他气体分子发生充分多次的碰撞，而且从碰撞结果看充满了随机性。所以它几乎是完全无序、各向同性的。