射影几何视角下的圆锥曲线（高中）

贡献者：欄、停敘

预备知识　圆锥曲线的统一定义，圆锥曲线与圆锥

　　之前用 “焦点–准线” 来定义圆锥曲线的探索中，已经把椭圆、双曲线和抛物线统一在一个框架下了，不过还有两个问题尚待解决：

既然用抛物线的定义统一了椭圆和双曲线，那么反过来，能不能也把抛物线纳入椭圆和双曲线的定义方式中？
在推导的过程中，曾经出现过 “焦点在无穷远处” 或者 “准线在无穷远处” 这样的说法。到底是什么意思？无穷远并不是一个具体的点，那怎么理解这种说法？

　　在高中的数学体系中，这类问题很难得到直接解释。但在一个叫 “射影几何” 的视角下，它们都可以变得清晰起来。虽然射影几何属于超纲内容，大多数教材和教师也并不涉及，但它恰恰能提供一种更完整的方式，把所有圆锥曲线背后的联系统一起来。特别是 “焦点–准线” 的定义为什么能够覆盖所有圆锥曲线，以及前面提到的两个问题，在这个视角下能够看得更透彻。

　　这一篇会简单介绍射影几何中最关键的想法，不涉及太多技术细节。就算只是作为一次短暂接触的初步了解，也能为整个圆锥曲线的结构提供一个更完整的背景，同时感受到数学统一性的魅力。

1. 平行线可以相交吗？

　　从初中就开始接触的 “几何”，其实指的是欧几里得几何（Euclidean Geometry，欧氏几何）的体系。这个体系的规则听上去非常自然，比如：

两条平行线永远不会相交；
一条直线可以无限延伸；
平面上的每一个点都表示一个具体的位置。

　　这些看似理所当然的规则，其实是从人们的日常经验中抽象总结出来的。整个中学阶段的几何学习——无论是平面几何、解析几何，还是立体几何和函数图像，都是在这套逻辑体系之下进行的。

　　可是真实世界中一些肉眼可见的现象，却似乎在挑战这种 “常识”。比如，在铁轨之间远眺时，两条原本平行的铁轨，看起来竟然在远方逐渐靠近，最后仿佛汇聚到一个点上；又比如仰头站在高楼下，两面垂直上升的墙体，也好像在天际会合于某个点。

图 1：平行轨道逐渐靠拢

图 2：仰望高楼时墙体汇合

　　有人可能会说，这只是视觉上的错觉而已。但问题在于，这种现象几乎每个人都能看见。如果希望一个几何系统能够更贴近人眼所看到的真实景象，就必须接受一个看起来有些 “违反常识” 的结论——平行线是可以相交的。而这就已经超出了欧氏几何所能描述的范围，毕竟，“平行线永不相交” 被写入第五条公理，是整个欧几里得几何体系的重要基础。一旦这条公理不再成立，人们自然会感到不安：如果连几何的根基都被动摇了，这个体系还能继续成立吗？

　　事实上，早在文艺复兴时期，这类现象在艺术领域就已经引起了注意。15 世纪初的艺术家 布鲁内莱斯基（Filippo Brunelleschi）从绘画的角度出发，首次提出了线性透视法。这种方法通过把视觉上平行线的 “交点” 设定为 “消失点” 来还原远近关系，让观者仿佛能够 “走进” 画中。自此，绘画不再是平面的拼图，而成为可以表现深度和距离的 “窗口”。

　　线性透视法的广泛应用，不仅改变了艺术的表达方式，也促使数学家重新思考几何的基础。事实上，在欧氏几何中，许多定理都需要分开讨论 “相交” 与 “平行” 的情况，这让整个体系在表达上显得不够统一，也缺乏美感。这种不够协调的逻辑结构，也促使数学家开始尝试突破原有框架。18 世纪，数学家 鲍耶伊（Giovanni Girolamo Saccheri）试图证明第五公设可以从其他公设中推导出来，但最终没有成功。然而，正是这次失败，意外地打开了通往一个全新几何世界的大门：非欧几何（Non-Euclidean Geometry）由此诞生。

　　后面要介绍的射影几何（projective geometry）就描绘了 “画家眼中的几何”，作为非欧几何的一种，它不再着眼于长度或角度等度量信息，而是更关注图形之间的位置、交点等关系。

2. 射影几何的基本结构

　　为了把前面提到的 “消失点” 等视觉现象纳入这个新的几何体系，使这些看似 “违反规则” 的现象可以被理解、推导，甚至计算，射影几何必须囊括前面得到的这几个基本观点：

无穷远处的点是 “存在” 的，不能直接忽略；
从一个视点向远方看时，所有方向上的无穷远点会排成一条线（也就是图 1 中的地平线）；
平行线会在在无穷远处相交。

　　在这种新视角下，欧几里得几何中那些常见的 “例外” 情况变得自然起来：平行线不再是 “不会相交” 的特殊情况，而是像其他直线一样，只不过它们的交点在无穷远处；无穷远点不再是抽象设想，而成为几何体系中实实在在的一部分。换句话说，那些被欧氏几何排除在外的元素，恰恰构成了统一几何结构的关键。

　　就像欧氏几何以平面为基础展开研究一样，射影几何也构建了自己的研究空间，称为射影平面（Projective Plane）。普通的欧氏平面 $\mathbb{R}^2$ 并不包含无穷远点，就像实数轴是无限延伸的，但本身却没有 “最远” 的点一样，即 $\mathbb{R} = (-\infty, +\infty)$。不过在数学中，为了研究一些极限情况，人们引入了一个称为超实数（hyperreal numbers）的集合，记作 $^*\mathbb{R}$，其中就包括了无穷大。射影平面的处理方法类似，为了满足前面的要点，在欧氏平面基础上额外引入了无穷远点（points at infinity）。于是，就像通过数轴与直线等价的实数变成了超实数那样，在射影平面中，直线不再如欧氏几何中那样无限延伸，而是朝着某个方向延伸并，最终在某个无穷远点 “结束”。

　　这时，一个自然的问题是，直线在欧氏几何中是向两侧无限延伸的，那么，这里直线向两边延伸之后到达的两个无穷远点的关系是什么？射影几何给出的答案是，把正无穷和负无穷 “粘合” 为同一个点”，从而使得每条直线在无穷远处 “闭合” 为一个 “环”。于是，一条直线与一个无穷远点构成了一条实射影直线（real projective line），后文所说的直线，除了 “无穷远直线” 之外，都是指实射影直线。

图 3：直线从两侧闭合于同一个无穷远点

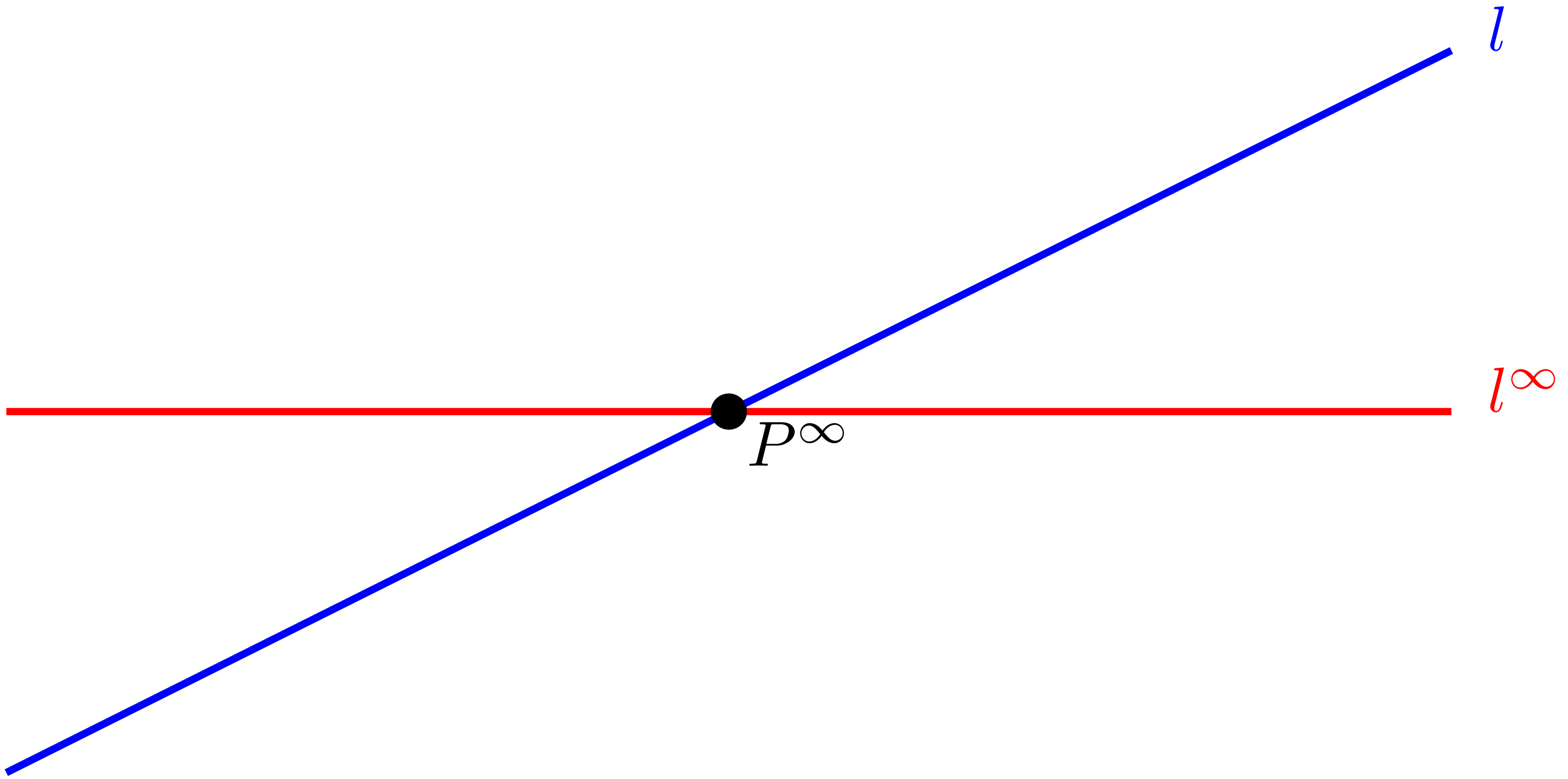
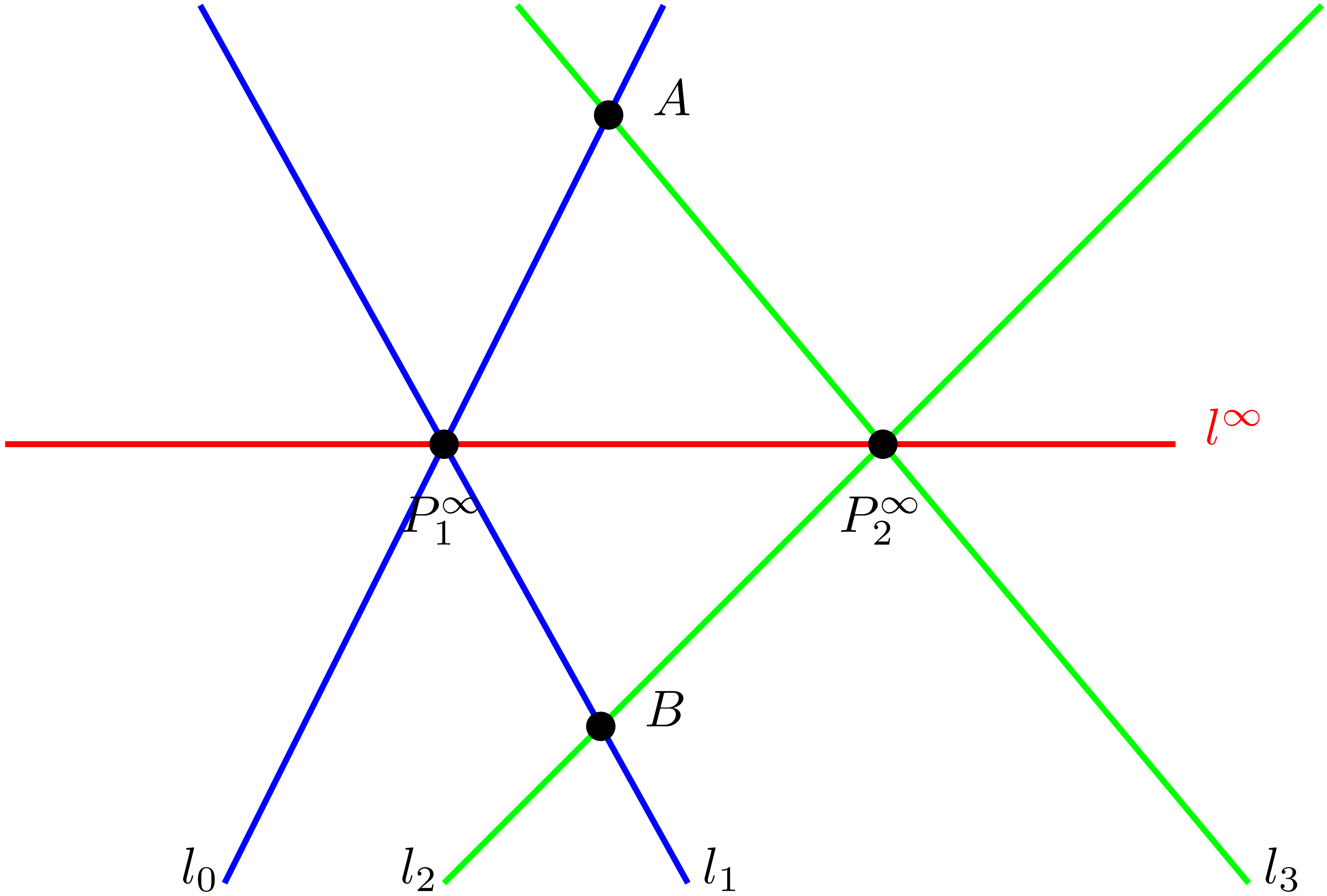
　　当然，光是加入一些 “远方的点” 并不会带来本质上的不同。关键是：这个体系如何组织这些点与其他元素之间的关系。射影几何的一个核心设定是：所有方向相同的直线，在无穷远处相交于同一个点。也就是说，朝着相同方向延伸的所有平行线，共用一个无穷远点。而因为方向可以连续变化，不同方向就对应着一整条连续的无穷远点，这条 “由所有无穷远点组成的直线” 就被称为无穷远直线（line at infinity），通常记作 $l^\infty$。如图 4 所示，任意两条直线都存在一个交点¹，当交点在无穷远直线上时，称这两条直线平行。

图 4：平行直线相交于同一无穷远点

　　之前说的一切内容，都只是复现了前面照片中对应的视觉特征。而建立射影几何的一个目标就是把欧氏几何中那些看起来 “不直观” 或者 “难处理” 的关系，转化为在射影几何中可以更自然理解、更加统一的结构。一个几何元素从一般平面变到射影平面的过程称为射影变换（projective transformation）。

　　 19 世纪初，法国数学家让-维克托·彭赛列（Jean-Victor Poncelet）在俄国战俘营中完成了他的代表作《论图形的摄影性质》（Traité des propriétés projectives des figures）。在这部著作中，他首次系统提出了投影不变性（invariance under projection）和对偶原理（principle of duality）这两个奠定射影几何基础的重要思想。这一思想打破了古典欧几里得几何中对 “形状” 的执着，把几何研究的焦点从 “看上去的样子” 转向了 “结构中的本质”。

　　在研究变换时，最重要的是确定哪些属性在变换前后仍然保持不变，也就是所谓的 “不变量”。这些不变量是判断图形结构在变换前后是否本质相同的依据。数学家们发现射影几何中最核心的两个不变量是：

共线性（collinearity）：原本在一条直线上的点，经过变换之后仍然在同一条直线上。这一性质保证了直线结构在变换中不被破坏，是最基本的结构不变量。
交比（cross ratio）：对于同一直线上的四个点 $A, B, C, D$，它们之间的交比定义为：
\begin{equation} (A, B; C, D) = \frac{AC \cdot BD}{AD \cdot BC}~. \end{equation}
这个比值在射影变换下保持不变，是射影几何中唯一保留下来的 “度量” 性质。它可以用来描述点之间的相对位置关系和排列顺序。

　　至此，射影几何打开了一种全新的视角，使 “无穷远” 不再是模糊不可触及的边界，而是被纳入几何结构中，成为其中自然的一部分。这回答了开头提到的第二个问题。

3. 齐次坐标与对偶原理

　　前面提到过，在射影几何的框架中，有一个非常重要的对偶原理（principle of duality），它说的是：在射影几何中，“点” 和 “直线” 在逻辑上具有对等的地位。也就是说，很多几何命题在将 “点” 与 “直线” 互换后，依然成立。例如，“两点确定一条直线” 这个命题，对偶之后变成 “两条直线确定一个交点”，而这两种说法在射影几何中都是正确的。正因为这种对称性，一旦某个命题被证明成立，它的对偶命题就可以直接成立，无需另作证明。这种结构极大地简化了命题的理解和推导过程。

　　那么，为什么点与直线可以对称地互换？要理解这一点，需要先引入一个射影几何中的重要工具：齐次坐标（homogeneous coordinates）。

　　在普通平面上，一个点通常用笛卡尔坐标 $(x, y)$ 表示，这种表示适用于有限远的点。但在射影几何中，还需要引入无穷远点，而普通坐标对此无能为力。为此，数学家们引入了齐次坐标，它用三个数 $(X, Y, Z)$ 来表示平面上的一个点，并通过以下关系与坐标 $(x,y)$ 对应：

\begin{equation} \begin{split} (X,Y,Z) \implies \left( \frac{X}{Z}, \frac{Y}{Z} \right),\qquad(Z\neq0)\\ (x,y)\implies\left( kx, ky,k \right),\qquad(k\neq0) \end{split}~. \end{equation}

　　也就是说，只要 $(X, Y, Z)$ 保持比例不变，它所代表的点就相同。例如，$(1, 2, 1)$、$(2, 4, 2)$ 和 $(10, 20, 10)$ 都表示平面上的同一个点 $(1, 2)$。这也是 “齐次” 这个名称的来源²。

　　特别地，当 $Z = 0$ 时，无法写成普通的 $(x, y)$ 形式，这样的点就正好对应了无穷远点。从而，整个平面中 $Z=0$ 的集合就构成了无穷远直线。通过齐次坐标，无穷远点可以被自然地纳入计算之中，不再需要像欧氏几何中那样刻意规避 “除以零” 的问题。

　　更重要的是，齐次坐标不仅可以用来表示点，也可以用来表示直线。例如，一个直线方程 $Ax + By + C = 0$，在齐次坐标下可以写作一个三元组 $(A, B, C)$。这意味着：点和直线都可以用同样的方式表示，完全对称。正因为这种对称结构，射影几何中可以给当前处理的平面建立一个对偶平面（dual plane）——在这个平面中，每一个 “点” 都对应着原平面中的一条 “直线”，而直线则对应着原来的一个点。两者互为镜像，联系的方式就是齐次坐标，而这就是对偶原理成立的根本原因。

　　随着 20 世纪几何体系的公理化发展，对偶原理也被正式纳入射影几何的基本逻辑中。特别是在平面射影几何中，点与直线的地位被严格对等地处理，所有公理与定理都对应着一个对偶形式。这种对称性不仅展现了几何体系的统一性，也体现了数学结构中的一种深层美感，使得几何不再局限于 “形状”，更是一种深刻的数学思想。

　　更进一步地，从更广阔的视角来看，对偶思想已经超越了几何本身。它推动了代数几何、拓扑学，乃至物理学中关于对称性与结构统一的研究。在处理复杂系统时，发现并利用 “可以对偶” 的结构，常常成为揭示深层规律的关键工具。

4. 射影几何视角下的圆锥曲线

　　接下来，将目光转向圆锥曲线。在传统几何中，利用平面截取三维空间中一个圆锥面得到的截线，称为圆锥曲线。在 “焦点-准线” 的统一定义中，由 “点-直线” 这个固定结构，在参数 $e$ 不同的情况下形成的曲线，称为圆锥曲线。但无论是空间切割中的平面的截取角度，还是焦点—准线的定义中距离的比值，它们本质上都依赖于度量（metric）。

　　这些定义背后传达出一个共同信息是，几种圆锥曲线之间存在某种内在联系。那么，一个自然的问题就出现了：既然它们共享结构基础，为什么形态差异会如此显著？圆是一种封闭的曲线，所有点到中心的距离都相等，看上去对称、规整，仿佛一个完美的轮廓；椭圆虽然不再各向等距，但依然封闭，形状扁长，轨迹圆滑；抛物线则完全打开，朝一个方向无限延伸，它既没有封闭的边界，也没有对称的 “另一边”；而双曲线更是分裂成两个完全分离的分支，向着两个相反方向延展。

　　这种从紧闭到敞开、从一体到分裂的巨大视觉和结构差异，很难不让人怀疑它们是否真的是 “一类曲线”。而射影几何揭示了这背后的原因。

　　在之前的推导中可以发现，所有常见的圆锥曲线都可以表示为一个二次方程：

\begin{equation} Ax^2+Bxy+Cy^2+Dx+Ey+F=0~. \end{equation}

在高中阶段，为了简化处理，通常会设置 $B = 0$，但从整体上看，这个约束并不影响后续的讨论。

　　把研究范围扩展到射影几何时，需要使用齐次坐标对上述表达式进行推广。这样一来，圆锥曲线可以写作一个二次齐次方程：

\begin{equation} AX^2 + BXY + CY^2 + DXZ + EYZ + FZ^2 = 0~. \end{equation}

这就给出了圆锥曲线在射影几何的本质定义——圆锥曲线是射影平面上满足某个二次齐次方程的所有点所组成的集合。在这个定义下，所有非退化的圆锥曲线在射影几何中本质上是相同的，或者说射影等价的。那么，为什么这些曲线在欧氏平面上看起来却差异巨大？答案就在于它们与无穷远直线的交点情况不同。

图 5：无穷远直线的移动过程

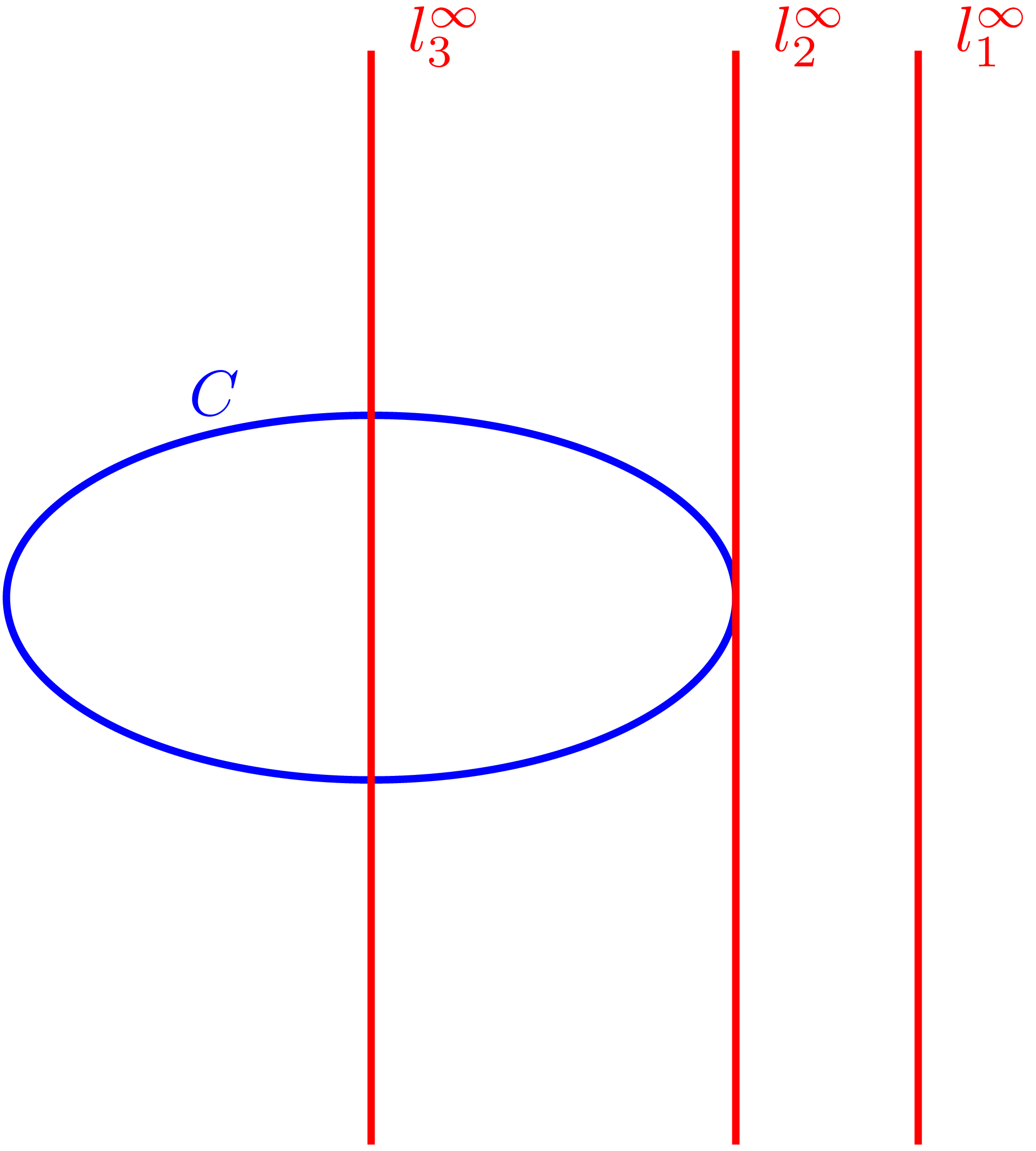
　　如图图 5 所示，假设曲线 $C$ 的所有参数均为正数，此时它在欧氏平面中表现为一个 “椭圆”。可以通过 “移动” 无穷远直线，来观察其与曲线 $C$ 的相交情况，从而理解不同类型圆锥曲线之间的关系：

开始时，无穷远直线并不与曲线 $C$ 相交，意味着曲线并未延伸到无穷远处，在射影几何中呈现为封闭的形态，即椭圆。
继续移动无穷远直线，使它逐渐 “靠近” 曲线 $C$，最终恰好与曲线 $C$ 在某个无穷远点相切，交点两侧各自趋于无穷，正好对应了抛物线的情况。
如果继续移动无穷远直线，让它穿过曲线，就会出现两个实交点，也就是说，一共有四个方向趋向了无穷远，而且，不同的交点两侧趋向于 “不同” 的无穷远。这正对应于双曲线。

　　也就是说，射影几何中对圆锥曲线的分类，不再依赖其封闭性、对称性或焦点结构，而是依据其与无穷远直线的相对位置关系：

椭圆是在射影平面中与无穷远直线没有实交点的圆锥曲线；
双曲线是在射影平面中与无穷远直线有两个实交点的圆锥曲线；
抛物线是在射影平面中与无穷远直线恰有一个交点的圆锥曲线。

　　从这个角度看，圆锥曲线只是同一个几何对象在不同视角下的表现。之所以只有三种形态，是因为无穷远直线与圆锥曲线之间只有三种几何位置关系：相交、相切、相离。而 $e=1$ 的抛物线恰好对应相切这一中间状态，自然成为三类之间的临界点。

　　这就顺理成章地回答了开头的第一个问题，从射影的角度来看，抛物线其实也有两个焦点，只不过其中一个焦点被 “送到了无穷远处”。椭圆的反射性质是 “经一焦点入、经另一焦点出”，而抛物线的反射路径平行于准线，实际上也可以看作是经由无穷远焦点出发。同样，双曲线之所以是反射后的反向延长线经过焦点，恰巧是因为反射的直线经过了无穷远直线。“另一个焦点” 其实可以看作是准线的对偶，它不是必须的，只是在对称性下自然出现。

　　此外，焦点–准线结构也可以自然地嵌入到射影几何的框架中。准线可以看作是一条射影直线，焦点是一点，离心率则可以通过某种射影不变量（例如交比）来表达。

　　总结一下，在引入射影几何后，对圆锥曲线的分类不再依赖 “开放或封闭”“角度或长度” 等度量性质，而是基于更本质的结构关系——它与无穷远直线的交点情况。圆锥曲线不再是几类不同的曲线，而是一个统一的几何实体的三种视角。每一条二次曲线的 “形态”，只是它与无穷远直线相对位置的表现，而不是来自曲线本身的 “本质差异”。

　　而这也意味着，只要施加一次合适的射影变换——可以简单地理解为调整观察者的视角，或者说 “移动无穷远直线”——就可以将任意一个圆锥曲线变换为另一个。这样的变换不会改变圆锥曲线的 “本质结构”，只改变它在眼中的 “外观”。正是这种统一性的出现，使得 “圆锥曲线与直线的关系” 成为研究圆锥曲线的核心主题之一。

　　除了统一形态外，射影几何还给圆锥曲线引入极点与极线。这一结构使得点与线之间出现了对称而优美的配对方式。具体地，对于一条给定的圆锥曲线，每一个点都对应一条极线，反之亦然。而极线与极点的关系正是从射影几何的角度把握圆锥曲线结构的精髓。它建立了一种由圆锥曲线决定的点与线之间的双射关系，从而为研究共轭点、对称结构、切线族等复杂现象提供了强有力的工具。

1. ^ 有些交点在纸外，没有画出。当然，如果有两条线，看上去是永远不相交的，也就是与无穷远直线的夹角相同，且与无穷远直线不交于同一点，则这个平面一定不是射影平面，也就是说它与给出的定义相冲突。
2. ^ 齐次函数是指输入同时乘以某个常数 $\lambda$，输出会乘以 $\lambda^k$，其中 $k$ 为齐次的次数。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。