群论中的证明和习题解答
贡献者: Siegfried; JierPeter; addis
1. 子群和正规子群
2. 群作用
例 2 迷向子群
问题来源请见习题 1 。
已知群 $G$ 作用在集合 $X$ 上,且对于 $x\in X$ 有 $G$ 的子集 $F_x=\{g\in G|g\cdot x=x\}$。
那么 $\forall g\in F_x$,$(g^{-1}g)\cdot x=e\cdot x=x$。又因为 $g\cdot x=x$,所以 $g^{-1}\cdot x=g^{-1}\cdot(g\cdot x)=(g^{-1}g)\cdot x=x$。
因此,$\forall g_1, g_2\in F_x$,有 $(g_1^{-1}g_2)\cdot x=g_1^{-1}\cdot x=x$,也就是说,$(g_1^{-1}g_2)\in F_x$。根据判别式定理 1 ,$F_x$ 构成 $G$ 的子群。
例 3 Burnside 引理
首先转写一个表达:$\sum_{g\in G}|X^g|=$“满足 $g\cdot x=x$ 的 $(g, x)$ 数量”$=\sum_{x\in X}|F_x|$。
由推论 3 ,$\sum_{x\in X}|F_x|=\sum_{x\in X} |G|/|O_x|=|G| \sum_{x\in X} 1/|O_x|$
现在关键是 $\sum_{x\in X} 1/|O_x|$ 是多少。显然,$\sum_{x\in O_x} 1/|O_x|=1$,也就是说 $1/|O_x|$ 在每一个 $O_x$ 上求和的结果是 $1$,那么它在整个 $X$ 上求和的结果,刚好就是所有轨道的数量 $|\{O_x|x\in X\}|$。
把以上结果整合,我们有:$\sum_{g\in G}|X^g|=|G|\cdot|\{O_x|x\in X\}|$。
例 4 Burnside 引理的应用
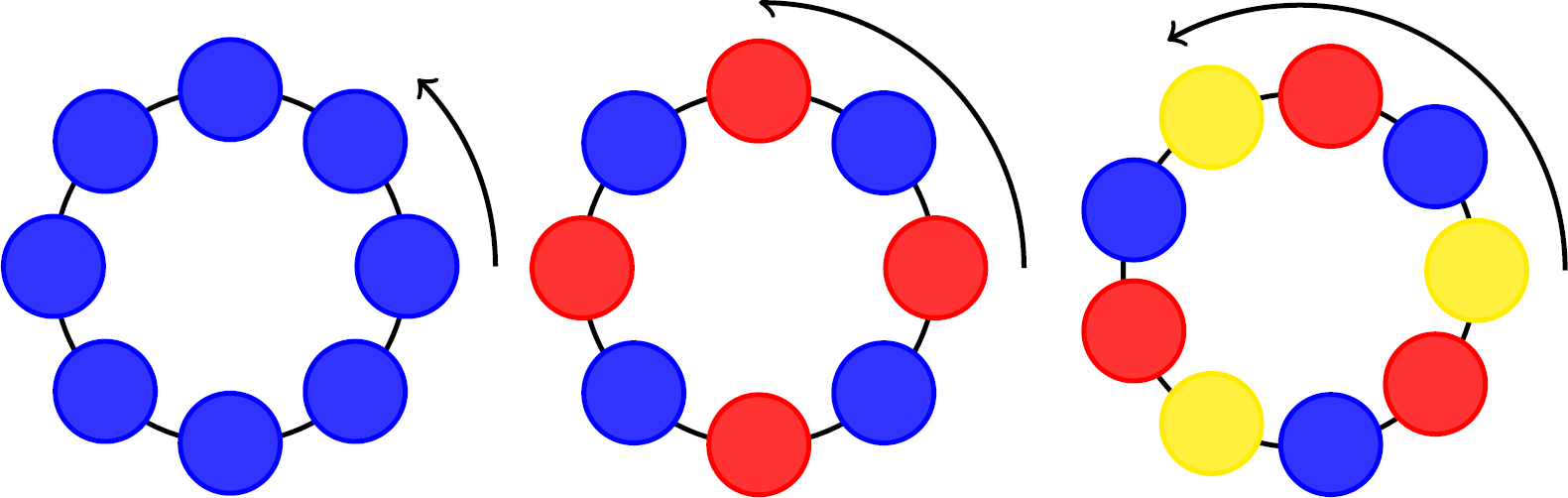
一堆珍珠有 $k$ 种颜色,且每种颜色的珍珠都足够多。其中取 $n$ 个珍珠串成一个手环,试问一共可以组成多少种不同的手环?旋转或翻转可以重合的情况算作一种。
我们给每个珍珠从 $1$ 到 $n$ 编号。设 $F=\{f_1,...,f_k\}$ 是不同颜色的集合,$X=F^n$ 是在固定顺序下,手环的所有颜色排列方案。显然在顺序固定情况下有 $k^n$ 种可能性,对应的是 $|X|=k^n$。我们现在要做的,是把所有旋转或翻转可以重合的情况,只保留记作一种。这等价于二面体群 $D_{2n}$ 作用在集合 $X$ 上。对于任意元素 $x_1,x_2\in X$,$x_1$ 在 $D_{2n}$ 作用下得到 $x_2$,等价于 $x_1,x_2$ 位于同一个轨道。而我们想求的去重复的不同排列数,也正是全部轨道的数量。
有了这样的思路,我们应用 Burnside 引理:首先对 $D_{2n}=\{e,d,...,d^{n-1},s,ds,...,d^{n-1}s\}$ 中的每个元素,计算其不动点的数量。(其中 $d$ 表示旋转,$s$ 表示翻转)
对于 $n$ 种翻转,当 $n$ 为奇数时,翻转轴一定经过一颗珍珠。对于这颗珍珠,以及翻转轴其中一侧的珍珠,一共有 $(n+1)/2$ 个,我们可以随意为它们选择颜色,从而得到该作用下 $k^\frac{n+1}{2}$ 个不动点。类似情况,当 $n$ 偶数时,有一半情况翻转轴经过两颗珍珠,一共有 $k^{\frac{n}{2}+1}$ 个不动点,另一半情况翻转轴不经过珍珠,一共有 $k^{\frac{n}{2}}$ 个不动点。
对于 $n$ 种旋转的情况(我们把保持不变的操作算作旋转 $0$ 次,当然也可以看成旋转 $n$ 次,即 $e=d^0$ 和 $d^n$ 表示同一种操作)。易见,当旋转一次时,当且仅当所有珍珠为同一颜色时,旋转后的颜色才会和旋转前重合。一共可能的颜色有 $k$ 种,对应着 $k$ 个不动点。对于一般情况 $d^r$,即旋转 $r$ 次,$1\le r\le n$,令 $m=\gcd(n,r)$。那么有 $k^m$ 种可能,随意为编号从 $1$ 到 $m$ 颗珍珠选择颜色,之后需要按照相同的样式,重复 $n/m$ 次直到刚好填满全部珍珠。于是我们得到旋转 $r$ 次时,不动点的个数为:$k^{\gcd(n,r)}$
最终,我们可以通过 Burnside 引理计算出轨道数,即制作不同手环的种类数。
例如,当 $n=4$,$k=2$ 时,一共有 $\frac{1}{8}\big((8+4+8+4)+(16+2+4+2)\big)=6$ 种,以及当 $n=5$,$k=3$ 时,一共有 $\frac{1}{10}\big((27+27+27+27+27)+(243+3+3+3+3)\big)=39$ 种。
例 5 自由群的一般性质
问题来源请见定理 2
设集合 $S$ 到群 $G$ 上有一个集合间的映射 $f$。我们来构造一个 $\varphi: F(S)\rightarrow G$ 的同态。
首先,由于 $\varphi$ 是 $f$ 的扩张,因此要定义 $\forall s\in S, \varphi(s)=f(s)$。
其次,由于 $\varphi$ 应为一个群同态,因此要定义 $\forall s_i\in S, \varphi({s_1s_2s_3\cdots})=\varphi(s_1)\varphi(s_2)\varphi(s_3)\cdots$。同时,还需要有 $\varphi(s^{-1})=\varphi(s)^{-1}$。
这样一来,$\varphi$ 的映射规则就确定下来了,并且容易验证它是一个群同态。因此这是唯一一个符合同态条件的扩张。
友情链接: 超理论坛 | ©小时科技 保留一切权利