贡献者: fengdalizzz
你可能在很多地方都听说过高斯光束,例如在光学课上,或者激光器的说明书里,但它们不会完整介绍高斯光束,因为这是高等光学的内容,即使高斯光束的应用非常普遍。本文将介绍高斯光束最重要的特性,也就是经过透镜等光学器件后,光斑的空间分布维持不变的这一特性,涉及近轴近似和惠更斯定理。
前言
光斑当然是应该有空间分布的。一开始学习的平面波的表达式是 $ \boldsymbol{\mathbf{E}} (x,y,z,t)= \boldsymbol{\mathbf{E_0}} \mathrm{e} ^{- \mathrm{i} \omega t}$,你可能觉得 $ \boldsymbol{\mathbf{E}} _0$ 可能是个常数,这显然是错误的,因为根据隔壁词条电场的能量,单位空间内平面波的能量是 $u=\frac{1}{2}\epsilon_0 \boldsymbol{\mathbf{E}} _0^{\;2}$,这是个常数,那么对 $u$ 全空间积分之后,就能得知该平面波携带了无穷大的能量,这显然是不合理的。那么 $ \boldsymbol{\mathbf{E}} _0$ 会不会只局限在某个局域呢?比如光斑只在一个圆形的截面里,就像我们日常看到的那样?这也是不行的,因为光会衍射,如果某个截面的光是局域的,那么就相当于在光路上放一个小孔,光就会在孔后形成衍射图样,当然,衍射图样是全空间的。这说明真实情况下光一定会有一个全空间分布。
结论
把一些结论和公式放在前面以供查阅:
- 高斯光束表达式:
\begin{equation}
E(x,y,z)=A\,H_l\left[\sqrt{2}x/w\right]H_m\left[\sqrt{2}y/w\right]\exp\left[- \mathrm{i} k\left(z+(x^2+y^2)/2q\right)\right]~
\end{equation}
- $q$ 的展开:
\begin{equation}
\frac{1}{q}=\frac{1}{R}- \mathrm{i} \frac{\lambda}{\pi w^2}~
\end{equation}
- $q$ 的变换:
\begin{equation}
q=\frac{Aq_1+B}{Cq_1+D}~.
\end{equation}
- 当光学器件两端的界面一致时:
\begin{equation}
AD-BC=1~
\end{equation}
- 零阶高斯光束
\begin{equation}
E(x,y,z)=A \mathrm{e} ^{- \mathrm{i} k(z+\frac{x^2+y^2}{2R})} \mathrm{e} ^{-\frac{x^2+y^2}{w^2}}~
\end{equation}
- 零阶高斯光束在空气、真空中的传播:
\begin{equation}
E(x,y,z)=\frac{w_0}{w}\exp-\frac{x^2+y^2}{w^2}\exp- \mathrm{i} k(z+\frac{x^2+y^2}{2R})\exp \mathrm{i} \phi ~
\end{equation}
\begin{equation}
\begin{aligned}
&w^{2}(z) =w_{0}^{2}\left[1+(z/z_{R})^{2}\right] \\
&R(z) =z\begin{bmatrix}1+(z_R/z)^2\end{bmatrix} \\
&\phi(z) =\tan^{-1} (z/z_{R}) ~
\end{aligned}~
\end{equation}
\begin{equation}
z_R=\frac{\pi w_0^2}{\lambda}~
\end{equation}
\begin{equation}
\theta_d=w_0/z_R=\frac{\lambda}{\pi w_0}~
\end{equation}
1. 近轴近似和 ABCD 矩阵
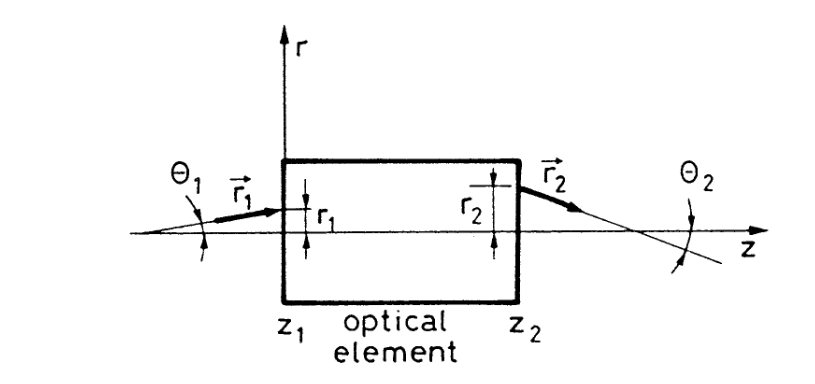
在谈论高斯光束之前需要先谈到一般情况下光线如何在光学器件上传播。为简单起见,这里只涉及几何光学的内容,也就是先忽略光斑的空间分布,把光看成是一条光线。如图 1 是一个任意的光学器件,例如是凸透镜,玻璃片或者什么都没有。
图 1:光学器件的定义。光线在 $z_1$ 平面以 $ \boldsymbol{\mathbf{r}} _1$ 角度入射,在 $z_2$ 平面以 $ \boldsymbol{\mathbf{r}} _2$ 角度出射。
我们定义了几个参数以表示这些光学器件对光线的作用,也就是图中的 $r_1,\theta_1$ 和 $r_2,\theta_2$(这里的 $r$ 是图中的那个标量。注意,我们需要标记一下标量的符号,图中 $r_1$ 和 $r_2$ 是正的,图中注明了 $r$ 轴;角度以旋转顺逆时针为准,所以图中 $\theta_1$ 是正的,$\theta_2$ 则是负的)。
我们认为 $r_2,\theta_2$ 和 $r_1,\theta_1$ 是有线性关系的,也就是有:
\begin{equation}
\begin{cases}
r_2=Ar_1+B\theta_1\\
\theta_2=Cr_1+D\theta_1~
\end{cases},
\quad\text{即:}\quad \begin{pmatrix}r_2\\ \theta_2\end{pmatrix} = \begin{pmatrix}A&B\\C&D\end{pmatrix} \begin{pmatrix}r_1\\ \theta_1\end{pmatrix} ~.
\end{equation}
这里就出现了所谓的 ABCD 矩阵(这命名有点随意)。对于特定的光学器件,A、B、C、D 都是常数。为什么会有这样的关系?这需要用到近轴近似,或者说,
小角极限。我们举例解释。
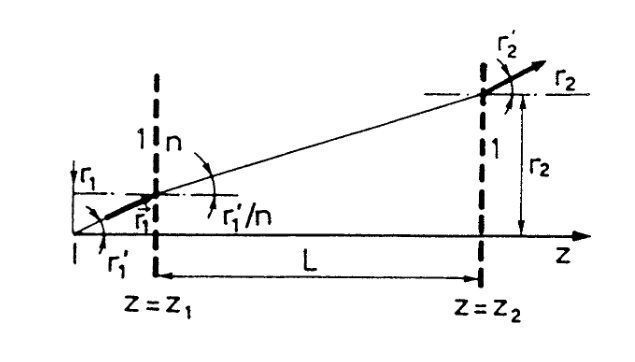
例 1
图 2:举例,一块“玻璃”
这是一块折射率 $n$ 的介质,长度为 $L$,那么就应当有:
\begin{equation}
r_2=r_1+L\cdot\tan\varphi\approx r_1+L\varphi\approx r_1+\frac{L}{n}\theta_1,\quad\theta_2=\theta_1~.
\end{equation}
所以该光学器件的 ABCD 矩阵就是:
\begin{equation}
\begin{pmatrix}1&L/n\\0&1\end{pmatrix} ~.
\end{equation}
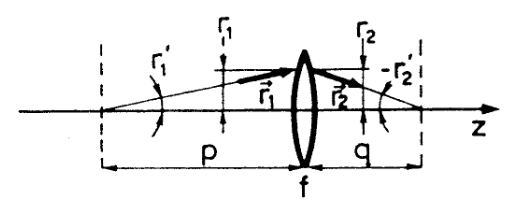
例 2
图 3:举例,一块理想薄透镜
这是一块焦距为 $f$ 的薄透镜。它很薄,所以有 $r_2=r_1$,同时,根据隔壁词条薄透镜,还有(不要忘记正负号):
\begin{equation}
\frac{1}{p}+\frac{1}{q}=\frac{1}{f}\quad\text{即:}\quad\frac{\theta_1}{r_1}+\frac{-\theta_2}{r_2}=\frac{1}{f}\quad\text{即:}\quad\theta_2=\theta_1-\frac{r_1}{f}~
\end{equation}
所以理想薄透镜的 ABCD 矩阵即为:
\begin{equation}
\begin{pmatrix}1&0\\-1/f&1\end{pmatrix} ~.
\end{equation}
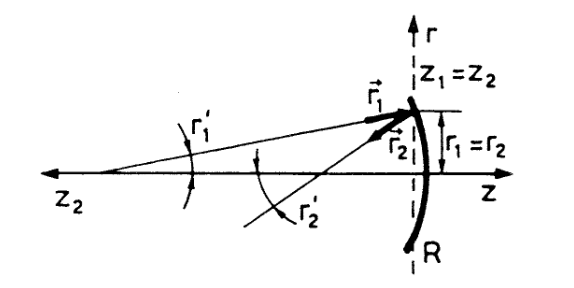
习题 1
图 4:举例,一块球面反射镜
证明半径为 $R$ 的球面反射镜的 ABCD 矩阵为:
\begin{equation}
\begin{pmatrix}1&0\\-2/R&1\end{pmatrix} ~.
\end{equation}
有了 ABCD 矩阵我们就可以很容易描述光学过程。显然,如果光线穿过了多个光学组件,那就相当于将它们的矩阵相乘。例如光线先穿过了长度为 $L_1$,折射率为 $n$ 的玻璃,接着又马上穿过了另一块长度为 $L_2$,折射率也为 $n$ 的玻璃,那么新的 ABCD 矩阵就是:
\begin{equation}
\begin{pmatrix}1&L_2/n\\0&1\end{pmatrix} \begin{pmatrix}1&L_1/n\\0&1\end{pmatrix} = \begin{pmatrix}1&(L_1+L_2)/n\\0&1\end{pmatrix} ~.
\end{equation}
太好了,两块一样的玻璃拼起来就相当于一块更长的玻璃!这说明我们的理论暂时还没有出错!
2. 近轴近似下的衍射
上面的推导都建立在 “光线” 的前提下,可惜光不能总看成一条直线,好在 ABCD 矩阵可以用在更多地方,比如衍射理论里。纯色光的传播的方程是亥姆霍兹方程,你可以从隔壁词条麦克斯韦方程组里轻易推导出来,它是:
\begin{equation}
(\nabla^2+k^2) \boldsymbol{\mathbf{E}} =0~.
\end{equation}
这里的 $ \boldsymbol{\mathbf{E}} $ 是指电场的空间分量,即 $ \boldsymbol{\mathbf{E}} (x,y,z)$。完整的表达式是 $ \boldsymbol{\mathbf{E}} (x,y,z,t)= \boldsymbol{\mathbf{E}} (x,y,z) \mathrm{e} ^{ \mathrm{i} \omega t}$,但我们研究的是空间分布,所以不需要管电场随时间的变化,下文中的 $ \boldsymbol{\mathbf{E}} $ 均指得是不带时间分量的那个,即 $ \boldsymbol{\mathbf{E}} (x,y,z)$。
此外,在我们的推导中,光线都是在均匀介质中的,没有色散,也没有非线性,所以式 17 成立,并且适用于电场任何一个空间分量,下文中将用 $E$ 来指代 $ \boldsymbol{\mathbf{E}} $ 的其中一个空间分量。
原则上根据式 17 就可以推导出高斯光束的表达形式,但是过程太抽象也太不物理了,后面我们再介绍这个方法。使用惠更斯-菲涅尔定律可以更形象地推导出高斯光束的空间分布方程,关于惠更斯定理的简明描述,可以参考隔壁词条惠更斯原理。我们需要用到它的数学形式,也就是:
\begin{equation}
E(x,y,z)=\frac{ \mathrm{i} }{\lambda}\iint_s E\left(x_1,y_1,z_1\right)\frac{ \mathrm{e} ^{- \mathrm{i} kr}}{r}\cos\theta\, dx_1 dy_1~
\end{equation}
该式子描述了 $z_1$ 平面的光斑,传播到 $z$ 平面时的电场的演化,也就是下图:
图 5:衍射示意图
接下来需要简化式 18 。使用近轴近似,也就是可以认为 $z_1$ 平面到 $z$ 平面的距离远远大于光斑本身的"大小",或者说,大部分的光组成的光斑的大小——实验上观测到的光斑往往只有几毫米大小,而光路却是分米级的——那么,可以认为 $\theta \approx 0$,也就是 $\cos \theta \approx 1$,$r \approx z-z_1$,但由于 $ \mathrm{e} ^{ \mathrm{i} kr}$ 中 $k$ 是一个很大的数,需要对其中的 $r$ 进行更精细的近似,也就是:
\begin{equation} \begin{aligned}
r=&\sqrt{\left(x-x_1\right)^2+\left(y-y_1\right)^2+\left(z-z_1\right)^2}\\
=&\left(z-z_1\right)\left(1+\frac{\left(x-x_1\right)^2}{\left(z-z_1\right)^2}+\frac{\left(y-y_1\right)^2}{\left(z-z_1\right)^2}\right)^{1/2}\\
=&z-z_1+\frac{\left(x-x_1\right)^2+\left(y-y_1\right)^2}{2\left(z-z_1\right)}~.\end{aligned}
\end{equation}
将这些近似代入,就可以化简为(不需要对 $z_1$ 积分):
\begin{equation}
E(x,y,z)=\frac{ \mathrm{i} \mathrm{e} ^{- \mathrm{i} k(z-z_1)}}{\lambda(z-z_1)}\iint_s E\left(x_1,y_1,z_1\right) \mathrm{e} ^{- \mathrm{i} k\frac{(x-x_1)^2+(y-y_1)^2}{2(z-z_1)}}\,dx_1dy_1~
\end{equation}
例 3 用亥姆霍兹方程的推导
从式 20 就可以看出,$E$ 的函数表达式中应该含有 $ \mathrm{e} ^{- \mathrm{i} kz}$ 这一项,我们把它提取出来,并令:
\begin{equation}
E(x,y,z)=u(x,y,z) \mathrm{e} ^{- \mathrm{i} kz}~.
\end{equation}
将
式 21 代入到
式 17 中去,就能得到:
\begin{equation}
\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right)u+\frac{\partial^2}{\partial z^2}u-2 \mathrm{i} k\frac{\partial}{\partial z}u=0~.
\end{equation}
中间的 $\frac{\partial^2}{\partial z^2}u$ 被认为由于 $u$ 是关于 $z$ 的缓变函数,所以可以舍去二阶项,只保留一阶项,也就是:
\begin{equation}
\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right)u-2 \mathrm{i} k\frac{\partial}{\partial z}u=0~.
\end{equation}
这个说法可能不是很好理解,但是式 23 和式 20 本质上是一样的,我们可以如下验证:首先,用式 21 改写式 20 得到:
\begin{equation}
u(x,y,z)=\frac{ \mathrm{i} }{\lambda(z-z_1)}\iint_s u\left(x_1,y_1,z_1\right) \mathrm{e} ^{- \mathrm{i} k\frac{(x-x_1)^2+(y-y_1)^2}{2(z-z_1)}}\,dx_1dy_1~
\end{equation}
接下来,把
式 24 代入到
式 23 即可验证。
3. 光学器件中的衍射
上述的衍射是发生在自由空间上的,也就是真空中。那么当光通过光学器件时,衍射公式会发生相应的变化,我们接下来将讨论衍射公式与 ABCD 矩阵的结合,最重要的就是得到式 18 中的相位项 $ \mathrm{e} ^{- \mathrm{i} kr}$。
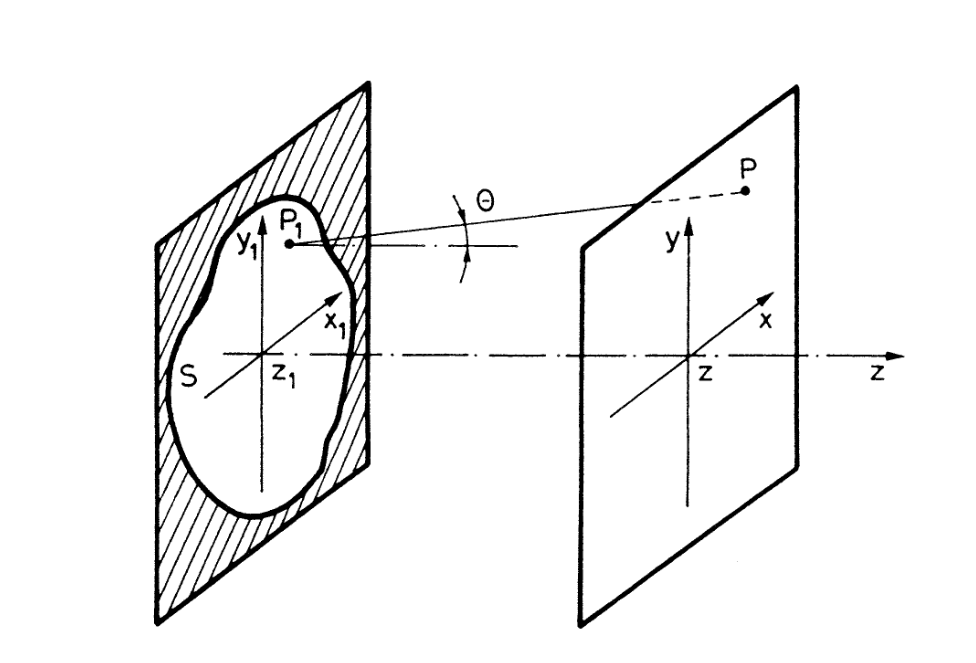
如图 6 (图片来自1。对参数的定义不同,所以图中的标注会有些许区别),假设衍射光中的一束光从点 $p_1$ 出发,在 $z_1$ 平面在 $r_1$ 处以 $\theta_1$ 角度入射,在 $z_2$ 平面以 $r_2,\theta_2$ 出射,最后到达点 $p_2$。
图 6:光线通过光线器件
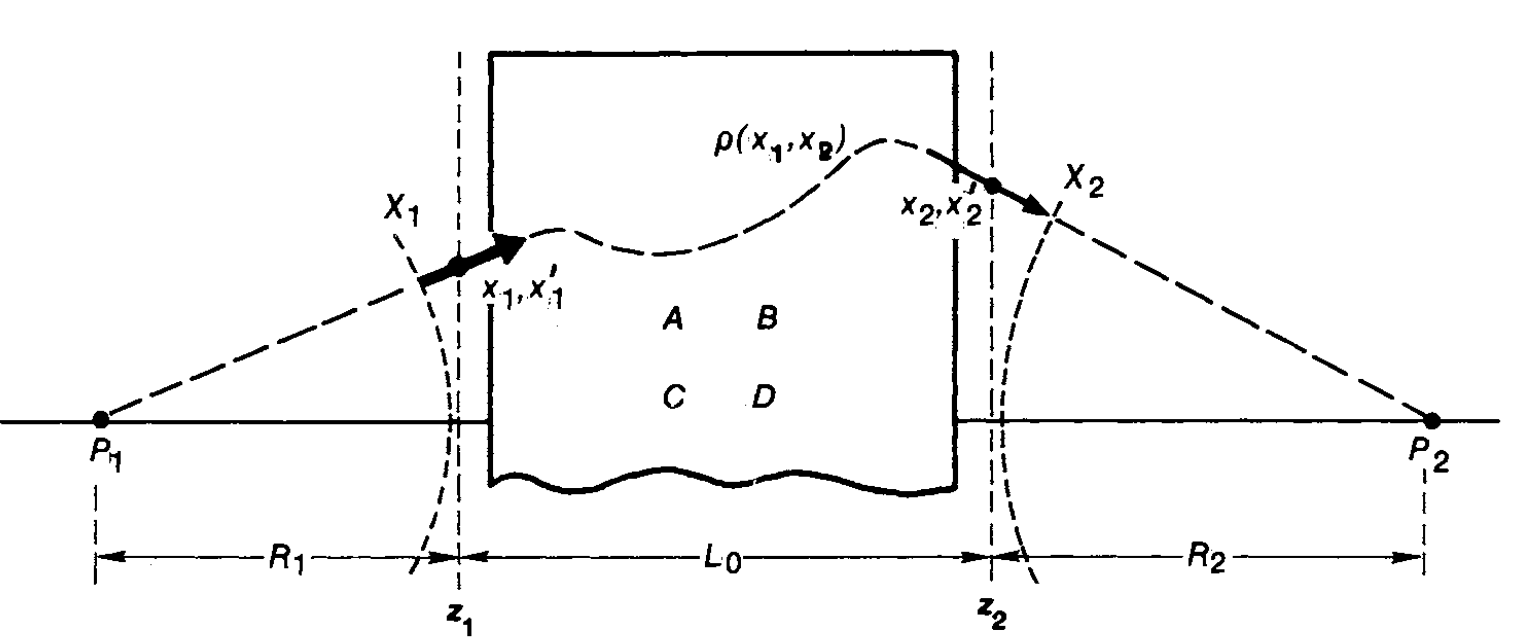
根据光程最短原理2,如果没有光学元件的存在,那么从点 $p_1$ 到点 $p_2$ 的光就只能走一种路径,也就是直线 $p_1p_2$。但光学元件的存在使得光走了另外一条路径,也就是图中的 $p_1-x_1-x_2-p_2$。但 $p_1x_1$ 明显大于 $R_1$,$x_2p_2$ 也明显大于 $R_2$,而光的两条路径都是最小光程路径,那么真相就只有一个,也就是光在通过光学器件时,相比于直接通过真空,光学器件对应的光程 “居然” 更小。该光程也就是前面提到的相位项 $ \mathrm{e} ^{- \mathrm{i} kr}$ 中的 $r$,现在来推导出它的具体数值。
由于两条路径的光程相等,就有:
\begin{equation} \begin{aligned}
&\quad\,\,\, p_1x_1+r+p_2x_2=R_1+L_0+R_2\\
&\Rightarrow r=L_0+R_1-\sqrt{R_1^2+r_1^2}+R_2-\sqrt{R_2^2+r_2^2}\\
&\text{利用一次近轴近似}\\
&\Rightarrow r\approx L_0-\frac{r_1^2}{2R_1}-\frac{r_2^2}{2R_2}\end{aligned} ~
\end{equation}
而
\begin{equation}
R_1\approx \frac{r_1}{\theta_1},\qquad R_2\approx \frac{-r_2}{\theta_2}~.
\end{equation}
观察
式 19 ,我们希望 $r$ 中只含有 $r_1$ 和 $r_2$。同时,注意到 ABCD 矩阵中有
\begin{equation}
AD-BC=1~,
\end{equation}
事实上,只要光学器件的两个表面的折射率一致——一般来讲都是空气,所以它总是成立的——则该式子成立。在接下来的推导中我们默认它成立。
根据定义,有:
\begin{equation} \begin{aligned}&\quad\,\,\,r_2=Ar_1+B\theta_1\\
&\quad\,\,\,\theta_2=Cr_1+D\theta_1\\
&\Rightarrow \theta_1=\frac{r_2-Ar_1}{B}\\
&\Rightarrow \theta_2=\frac{Dr_2-r_1}{B}\end{aligned} ~
\end{equation}
将
式 28 代入
式 26 再代回到
式 25 ,就能得到:
\begin{equation}
r\approx L_0+\frac{Ar_1^2-2r_1r_2+Dr_2^2}{2B}~
\end{equation}
这是二维时的推导,在这里我们直接写出三维时的表达式:
\begin{equation}
r\approx L_0+\frac{A(x_1^2+y_1^2)-2x_1x-2y_1y+D(x^2+y^2)}{2B}~
\end{equation}
那么,类似的我们就可以直接写出 $u(x,y,z)$ 形式的经过光学器件的衍射方程:
\begin{equation}
u(x,y,z)=\frac{ \mathrm{i} }{B\lambda }\iint_s u\left(x_1,y_1,z_1\right) \mathrm{e} ^{- \mathrm{i} k\frac{A(x_1^2+y_1^2)-2x_1x-2y_1y+D(x^2+y^2)}{2B}}\,dx_1dy_1~
\end{equation}
这就是著名的柯林斯(Collins)公式。这里一维到二维的转换可能难以理解,该公式的详细推导可以自行查阅。可以简单进行一下验证。真空其实是玻璃的 “一种”,其折射率为 1,那么它的 ABCD 矩阵也就是:
\begin{equation}
\begin{pmatrix}1&L\\0&1\end{pmatrix} ~.
\end{equation}
将它代入到
式 31 里,就能得到:
\begin{equation}
u(x,y,z)=\frac{ \mathrm{i} }{L\lambda }\iint_s u\left(x_1,y_1,z_1\right) \mathrm{e} ^{- \mathrm{i} k\frac{(x-x_1)^2+(y-y_1^2)}{2L}}\,dx_1dy_1~
\end{equation}
鉴于 $L=z-z_0$,所以上式实际上就是
式 24 。所以
式 24 其实是
式 31 的一种特例。
4. 零阶高斯光束
回想最开始时的描述,高斯光束通过光学器件时,光斑的空间分布不变,也就是说式 31 中的 $u(x,y,z)$ 应该和 $u(x_1,y_1,z_1)$ 具有类似的函数表达式。我们现在需要找到这样一个合适的函数。观察式 31 :
\begin{equation}
u(x,y,z)=\frac{ \mathrm{i} }{B\lambda }\iint_s u\left(x_1,y_1,z_1\right) \mathrm{e} ^{- \mathrm{i} k\frac{A(x_1^2+y_1^2)-2x_1x-2y_1y+D(x^2+y^2)}{2B}}\,dx_1dy_1~
\end{equation}
一般来说光学器件的通光孔径一般都能覆盖绝大多数的光斑,所以积分区域 $s$ 可以改成全空间,那么此时式中的 $ \mathrm{e} ^{- \mathrm{i} kx_1}dx_1$ 就相当于给函数做傅里叶变换,而高斯曲线(正态分布标准曲线)在傅里叶变换后函数形式是基本不变的,可以参考词条傅里叶变换。同时式中的 $ \mathrm{e} ^{- \mathrm{i} kD(x^2+y^2)}$ 也给出了类似的提示。那么我们就可以猜测 $u$ 的一种可能的形式:
\begin{equation}
u(x_1,y_1,z_1)= \mathrm{e} ^{- \mathrm{i} k\frac{x_1^2+y_1^2}{2q_1}}~
\end{equation}
其中的 $q_1=q_1(z)$,是关于 $z$ 的函数。这里的 $u$ 没有归一化处理。把它代回到
式 31 中的 $u(x_1,y_1,z_1)$,进行一些简单的重新排列式子,就能得到:
\begin{equation}
\begin{aligned}
u(x,y,z)&=\frac{ \mathrm{i} }{B\lambda }\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}dx_1dy_1\, \mathrm{e} ^{- \mathrm{i} k\frac{x_1^2+y_1^2}{2q_1}} \mathrm{e} ^{- \mathrm{i} k\frac{A(x_1^2+y_1^2)-2x_1x-2y_1y+D(x^2+y^2)}{2B}}\\
&=\frac{ \mathrm{i} }{B\lambda } \mathrm{e} ^{- \mathrm{i} k\frac{D}{2B}(x^2+y^2)}\times \int_{-\infty}^{+\infty}dx_1\, \mathrm{e} ^{- \mathrm{i} k\frac{x_1^2}{2q_1}} \mathrm{e} ^{- \mathrm{i} k\frac{Ax_1^2-2x_1x}{2B}}\\
&\times \int_{-\infty}^{+\infty}dy_1\, \mathrm{e} ^{- \mathrm{i} k\frac{y_1^2}{2q_1}} \mathrm{e} ^{- \mathrm{i} k\frac{Ay_1^2-2y_1y}{2B}}\\
&=\frac{ \mathrm{i} }{B\lambda } \mathrm{e} ^{- \mathrm{i} k\frac{D}{2B}(x^2+y^2)}\times \int_{-\infty}^{+\infty}dx_1\, \mathrm{e} ^{- \mathrm{i} k(\frac{1}{2q_1}+\frac{A}{2B})x_1^2} \mathrm{e} ^{ \mathrm{i} k\frac{x}{B}x_1}\\
&\times \int_{-\infty}^{+\infty}dy_1\, \mathrm{e} ^{- \mathrm{i} k(\frac{1}{2q_1}+\frac{A}{2B})y_1^2} \mathrm{e} ^{ \mathrm{i} k\frac{y}{B}y_1}~
\end{aligned} ~
\end{equation}
积分符号内都是傅里叶变换,所以可以直接带入公式,公式来源是隔壁词条
傅里叶变换,即:
\begin{equation}
\int_{-\infty}^{+\infty}dx_1\, \mathrm{e} ^{- \mathrm{i} k(\frac{1}{2q_1}+\frac{A}{2B})x_1^2} \mathrm{e} ^{ \mathrm{i} k\frac{x}{B}x_1}=\frac{\sqrt{2\pi}}{\sqrt{2 \mathrm{i} k(\frac{1}{2q_1}+\frac{A}{2B})}}\exp{\frac{ \mathrm{i} k\frac{x^2}{B^2}}{2(\frac{1}{q_1}+\frac{A}{B})}}~
\end{equation}
也就是:
\begin{equation}
u(x,y,z)=\frac{1}{\frac{B}{q_1}+A} \mathrm{e} ^{- \mathrm{i} k\frac{x^2+y^2}{2q}}~
\end{equation}
其中 $1/q=\frac{D}{B}-\frac{1}{\frac{B^2}{q_1}+{BA}}$,再次利用 $AD-BC=1$,可以得到:
\begin{equation}
q=\frac{Aq_1+B}{Cq_1+D}~.
\end{equation}
式 38 的函数形式与式 35 一致,这证明了我们的猜测是正确的:式 35 这样一个分布的光就是我们要找的,通过光学元件后光斑分布不变的一种光,写回成 $E$ 的形式,也就是:
\begin{equation}
E(x,y,z)=A \mathrm{e} ^{- \mathrm{i} k(z+\frac{x^2+y^2}{2q(z)})}\qquad (A\text{是归一化系数})~
\end{equation}
继续深入。观察上式,可以发现相位 $z+\frac{x^2+y^2}{2q(z)}$ 非常类似于我们之前经常使用的近轴近似的结果。联想到球面波的形式 $E= \mathrm{e} ^{- \mathrm{i} kR}/R$,对相位的 $R$ 进行近轴近似可以得到 $R\approx z+\frac{x^2+y^2}{2R}$,两者的形式非常类似。我们有理由认为式 40 所代表的光也是一种球面波,但球面半径是复数。将 $1/q(z)$ 分成:
\begin{equation}
\frac{1}{q}=\frac{1}{R}- \mathrm{i} \frac{\lambda}{\pi w^2}~
\end{equation}
那么
式 40 就可以写成:
\begin{equation}
E(x,y,z)=A \mathrm{e} ^{- \mathrm{i} k(z+\frac{x^2+y^2}{2R})} \mathrm{e} ^{-\frac{x^2+y^2}{w^2}}~
\end{equation}
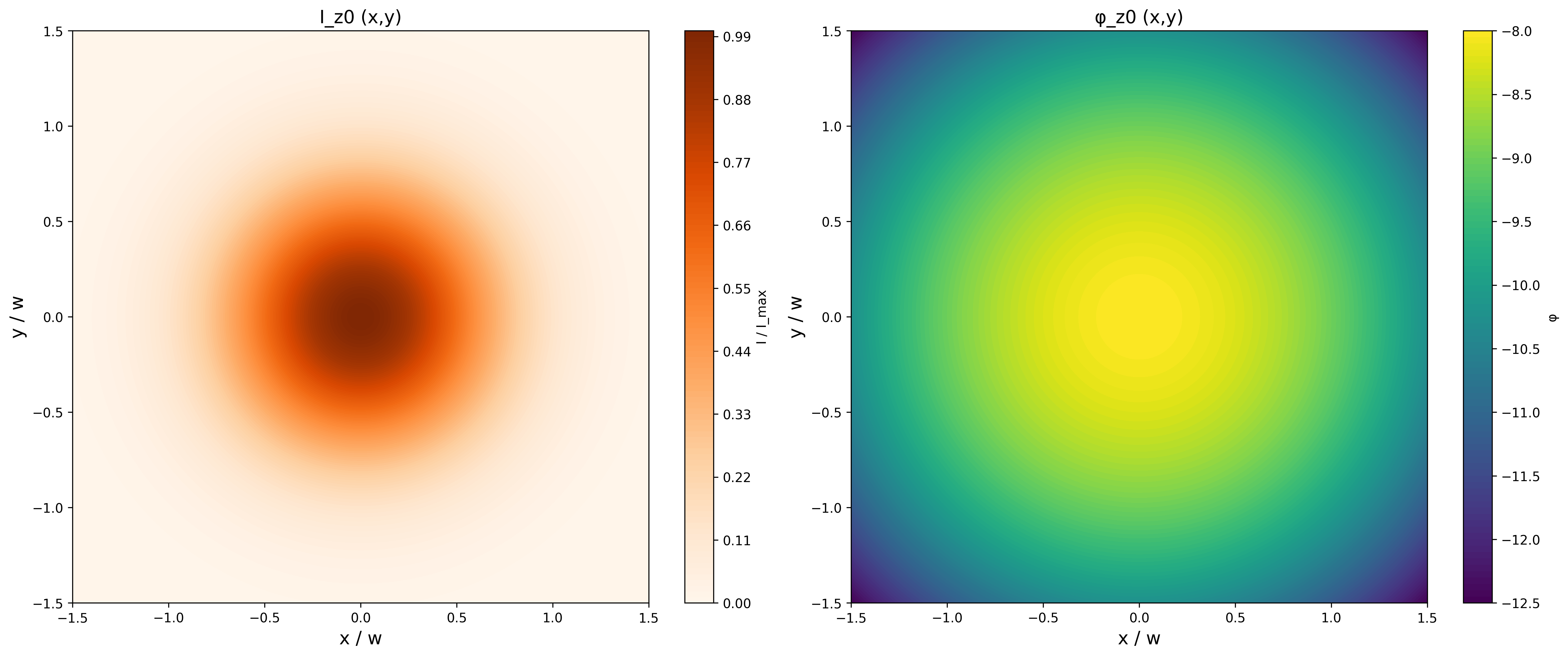
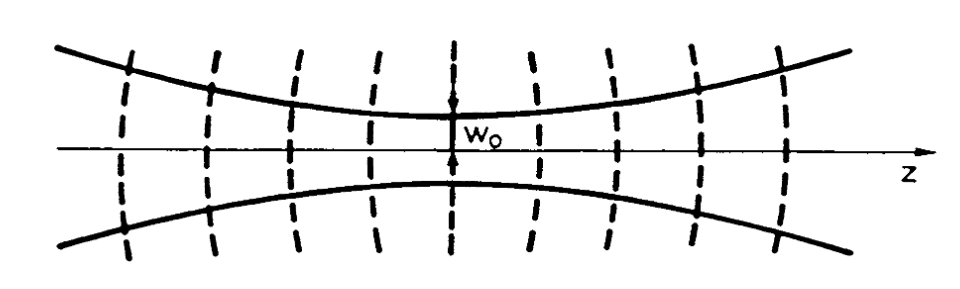
现在一切都明了了。式 42 所代表的就是零阶高斯光束,其相位项是和球面波一致的,但相位项前面乘上了一个高斯分布的因子。$R$ 即为球面半径,如果 $R$ 足够大,相位项就退化为平面波;而 $w$ 代表的就是高斯分布的腰宽,绝大多数的光都聚集在该范围内,形成我们看到的光斑。
可以做出在某一截面($z=z_0$)上的光强分布以及相位变化,能更加提示出其特点:
图 7
5. 零阶高斯光束的传播
如果你经常做光学实验,你就会发现其实即使不加透镜,激光器的出射光也会自己聚焦,或者以一个比例将光斑按传播距离发散;对激光使用透镜,光斑也不会像理想情况那样在某个位置聚焦成一个无限小的点。有了前面的理论基础,我们现在就能好好解释一下这个现象了。
激光器的出射光一般都是零模的高斯光。假设一束零模高斯光在空气中传播,也就是 $A=D=1,B=z,C=0$,那么根据和式 39 :
\begin{equation}
q=q_1+z~
\end{equation}
假设在 $z=0$ 处 $R=+\infty$:
\begin{equation}
\frac{1}{q_1}=- \mathrm{i} \frac{\lambda}{\pi w_0^2}~
\end{equation}
可以验证,这个假设相当于认为 $z=0$ 的光束类似平面波。
根据
式 38 ,经过简单的计算,就有:
\begin{equation}
u(x,y,z)=\frac{w_0}{w}\exp-\frac{x^2+y^2}{w^2}\exp- \mathrm{i} k\frac{x^2+y^2}{2R}\exp \mathrm{i} \phi ~
\end{equation}
其中:
\begin{equation}
w^2(z)=w_0^2\left[1+\left(\frac{\lambda z}{\pi w_0^2}\right)^2\right]~
\end{equation}
\begin{equation}
R(z)=z\left[1+\left(\frac{\pi w_0^2}{\lambda z}\right)^2\right]~
\end{equation}
\begin{equation}
\phi=\tan^{-1}\left(\frac{\lambda z}{\pi w_0^2}\right)~
\end{equation}
令:
\begin{equation}
z_R=\frac{\pi w_0^2}{\lambda}~
\end{equation}
可以简化这三条式子:
\begin{equation}
\begin{aligned}
&w^{2}(z) =w_{0}^{2}\left[1+(z/z_{R})^{2}\right] \\
&R(z) =z\begin{bmatrix}1+(z_R/z)^2\end{bmatrix} \\
&\phi(z) =\tan^{-1} (z/z_{R}) ~
\end{aligned}~
\end{equation}
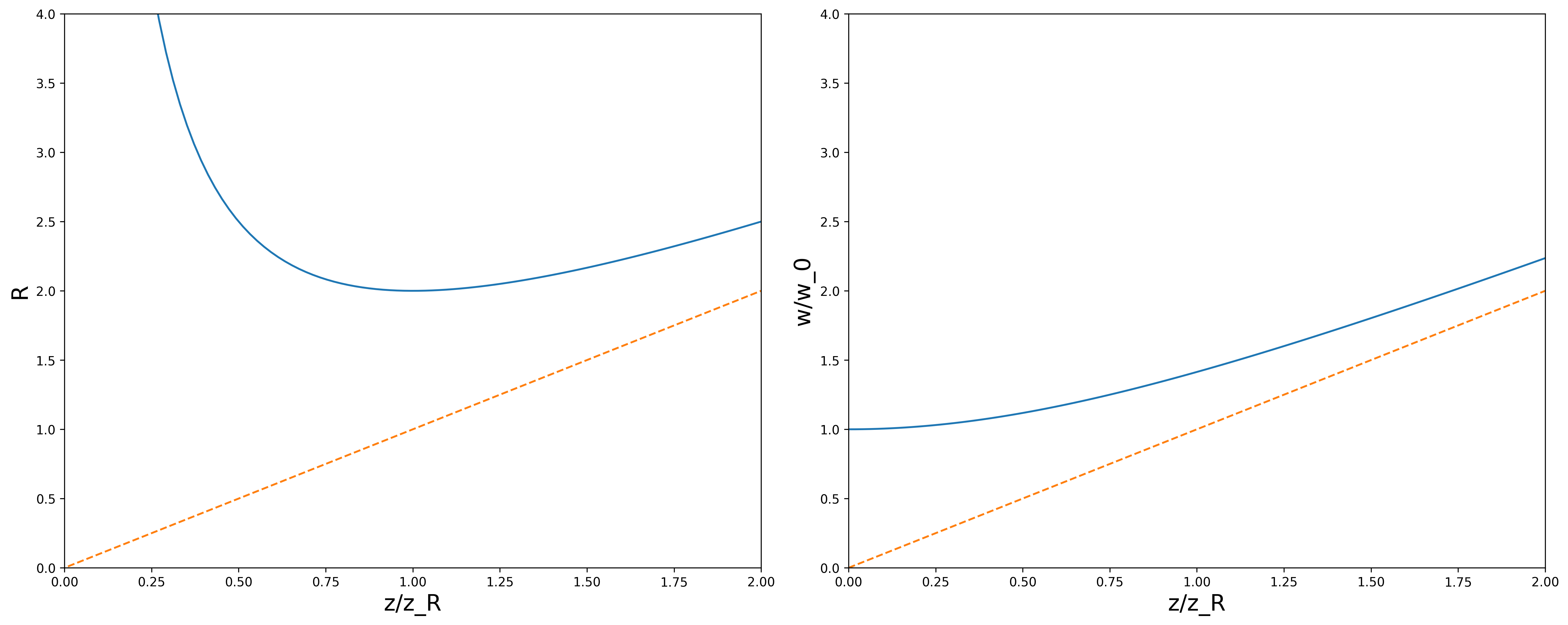
做出 $R$ 和 $w/w_0$ 随 $z$ 的变化图:
图 8
可以看到,$z=0$ 处 $R=+\infty$,这是我们所假设的,此时光束的相位项是平面波,在 $z$ 足够大时(注意,一般的红色激光笔的 $z_R$ 大约是 5m),$R\approx z$,$z=+\infty$ 时可以再次转为平面波;$w$ 在 $z=0$ 处有最小值,此后随 $z$ 均匀增大,也就是 $w\approx w_0 \,z/z_R$,那么就可以定义发散角:
\begin{equation}
\theta_d=w_0/z_R=\frac{\lambda}{\pi w_0}~
\end{equation}
根据以上信息可以作图:
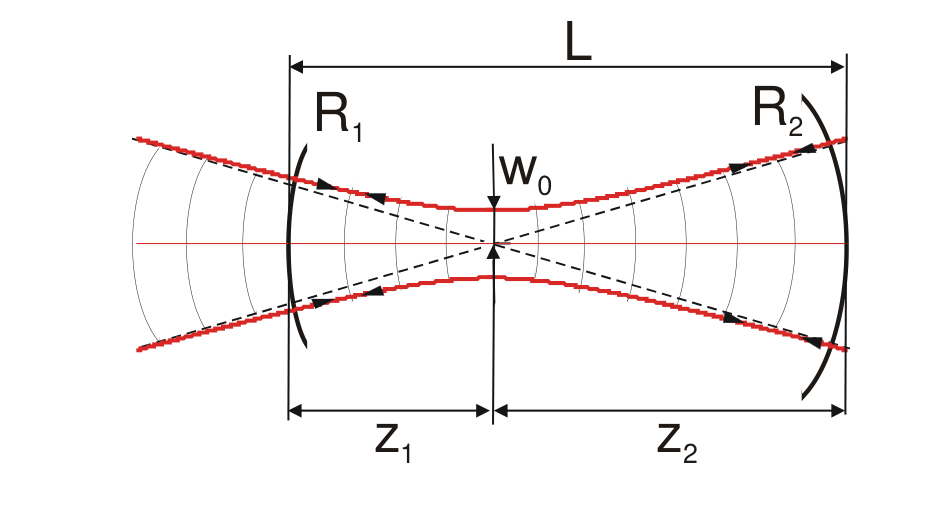
图 9:实线是腰宽,虚线是等相位面
从这张图就可以看到高斯光束的 “自聚焦效应”,同时,在光斑 “最小处”,等相位面是平面。
如果在光路中放置一个透镜,光束的聚集位置和光斑大小会发生更加复杂的变化。同样假设 $z=0$ 处光束的光斑最小,也就是 $R=+\infty$,在 $z=L_1$ 处放置一个透镜,光束通过透镜后传播了 $L_2$ 距离重新达到光斑最小状态,也就是在 $L_2$ 处聚焦。则 ABCD 矩阵为:
\begin{equation}
\begin{pmatrix}1&L_2\\0&1\end{pmatrix} \begin{pmatrix}1&0\\-1/f&1\end{pmatrix} \begin{pmatrix}1&L_1\\0&1\end{pmatrix} ~
\end{equation}
将矩阵代入到
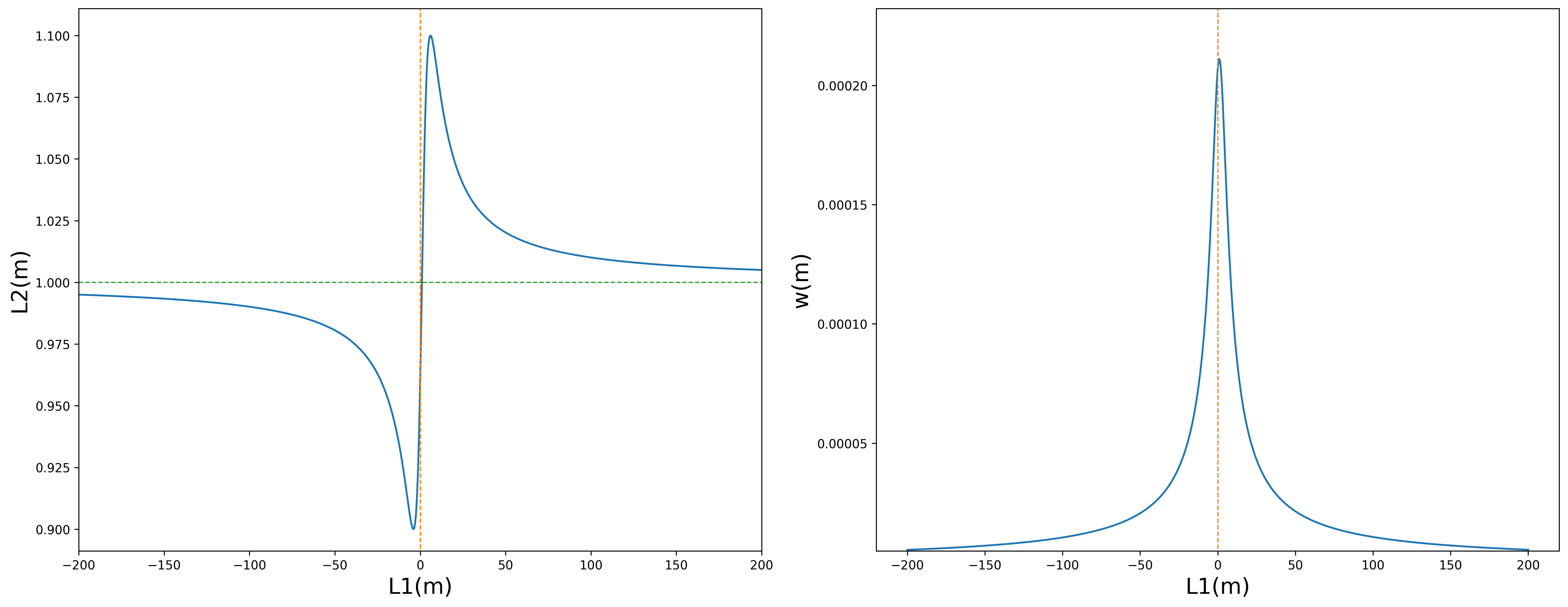
式 39 中,并且令 $ \operatorname{Re} {q}=0$,就可以得到 $L_2$ 的具体数值;将计算到的 $L_2$ 代入到 $q$ 的虚部中,就可以得到 $w$。可以绘制出 $L_2$ 和 $w$ 随透镜位置 $L_1$ 的变化(在具体的计算中,令 $z_R=5m,f=1m,\lambda=700nm$,也就是最常见的红色激光笔和透镜的参数):
图 10
观察计算结果可以发现,对于聚焦位置,似乎放置在 $z=0$ 处的透镜的效果最接近理想情况,也就是 $L_2=f$,因为此时入射到透镜的高斯光束接近平面波。但实际是 $L_2=f$ 的点与 $z=0$ 处有非常细微的差别,只有当 $L_1\to \pm\infty$ 时 $L_2$ 才趋于 $f$,因为此时高斯光才退化成平面波;同样的,在 $L_1\to \pm\infty$ 时高斯光才能被透镜聚焦成无限小的光斑,也就是 $w\to 0$。
例 4
为什么激光器总是打出高斯光束?这个问题很复杂,简单解释的话就是激光器的核心组件之一是谐振腔,激光需要在谐振腔中多次反射和传播。只有高斯光束这种经过光学器件而保持光斑分布不变的激光能通过谐振腔。高斯光就像是量子力学里的本征态,光学器件像是算符,只有本征态才能保证算符作用后形式不变。
图 11:谐振腔中的高斯光
6. 高阶高斯光束
在 4 节我们提到衍射方程中含有傅里叶变换,而零阶高斯光束就是傅里叶变换前后函数形式不变的一个函数。除此之外,厄米(Hermite)多项式与高斯函数的乘积也可以做到傅里叶变换前后函数的形式不变。比较容易证明的是:
\begin{equation}
\mathcal F[H_n(x) \mathrm{e} ^{-x^2/2}]=(- \mathrm{i} )^nH_n(k) \mathrm{e} ^{-k^2/2}~
\end{equation}
证明这个需要用到厄米多项式的生成函数,也就是:
\begin{equation}
\sum_n H_n(x)\frac{t^n}{n!}= \mathrm{e} ^{2xt-t^2}~
\end{equation}
未完成:继续推导需要更多的证明。
我们直接给出高阶的厄米高斯光束的函数形式:
\begin{equation}
u(x_1,y_1,z_1)=H_l\left[\sqrt{2}x_1/w_1\right]H_m\left[\sqrt{2}y_1/w_1\right]\exp\left[- \mathrm{i} k\left(x_1^2+y_1^2\right)/2q_1\right]~
\end{equation}
代入
式 31 中,能得到:
\begin{equation}
u(x,y,z)=\left[\frac{1}{A+(B/q_1)}\right]^{1+l+m}H_l\left(\frac{\sqrt{2}x}{w}\right)H_m\left(\frac{\sqrt{2}y}{w}\right)\times\exp- \mathrm{i} k\frac{\left(x^2+y^2\right)}{2q}~
\end{equation}
其中 $q$ 的变化和展开均与零阶高斯光束一致。
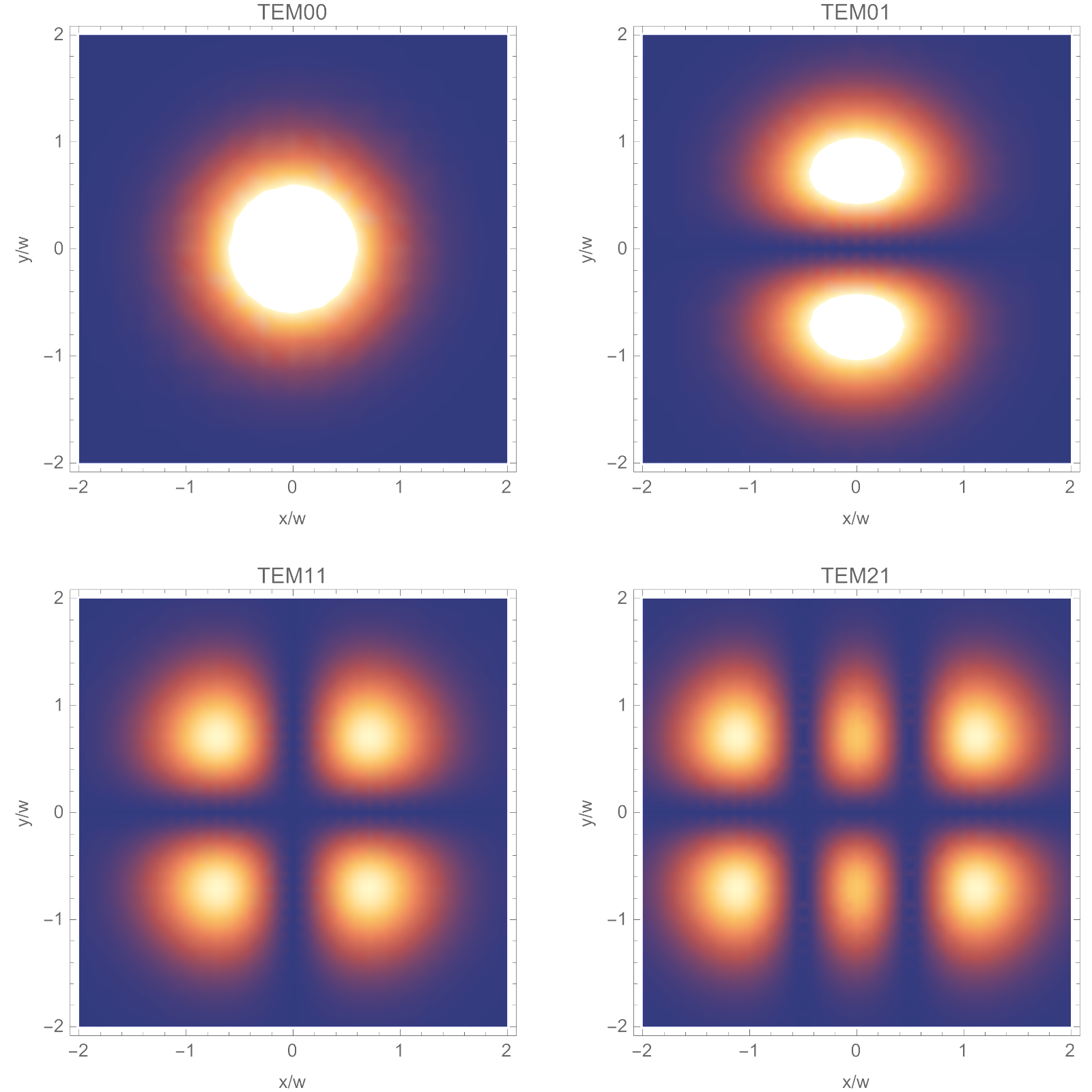
可以作出各个模式的高斯光束的光强分布图:
图 12
一般的激光器都被设定成发出零阶的高斯光束,如果你看到了其他模式的光,那么就应该考虑考虑维修激光器了。
1. ^ A.E. Siegman, Lasers (Oxford University Press, Oxford, U. K.), Chapt. 20.
2. ^ 光程最短原理的正确表述应该是光程平稳原理,光在两点间的光程是极小值或极大值,甚至是拐点。下面的推导是不严谨的,但推导的结果是正确的。
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。