EPR 佯谬与定域隐变量理论

                     

贡献者： _Eden_; addis

　　 1935 年，Einstein，Podolsky 和 Rosen 发表一篇名为《Can Quantum Mechanical Description of Physical Reality be Considered Complete》文章，以定域实在论为出发点论证量子力学的不完备性，以佯谬的形式对量子力学的哥本哈根诠释提出了批评。在这篇论文中 Einstein 谈到：“我不相信上帝会掷骰子。”（原文是 “I can't believe that God plays dice”。）

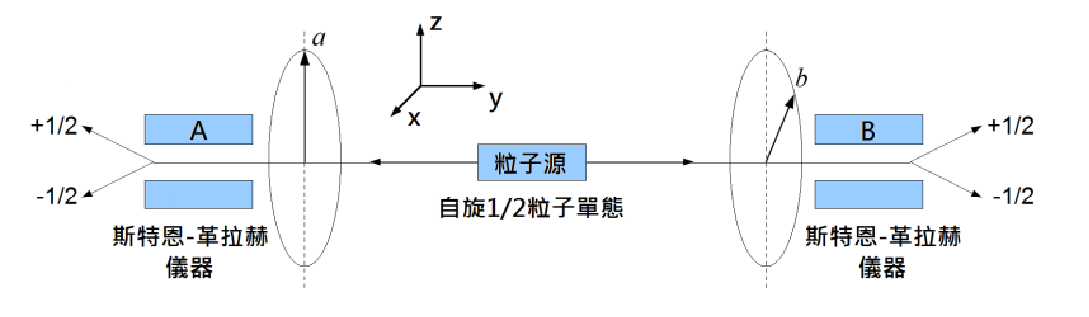
　　 EPR 佯谬是基于这样一个思想实验¹。我们有一个粒子源，它能够同时产生两个自旋 $1/2$ 的粒子（为了方便表述，下面假定它为电子）。单个电子的自旋方向是不确定的，但是粒子源保证了这两个电子的自旋总是相反的，即双电子体系的总自旋为 $0$。具体而言，双粒子波函数可以写为

　　 其中一个电子我们设为 $A$，它经过左侧的斯特恩–格拉赫²实验装置，被测量其自旋沿某一方向上的投影分量。根据量子力学的坍缩假设，电子的状态会坍缩到沿这一方向上自旋为 $1/2$ 或 $-1/2$ 的本征态，它们是相应自旋算符的本征态：例如可以是 $S_z$ 或 $S_x$。以 $S_z$ 的两个本征态 $ \left\lvert \uparrow \right\rangle , \left\lvert \downarrow \right\rangle $ 为自旋空间的基底，那么自旋算符在数学上可以写为泡利算符乘以 $1/2$。（本文中我们采用自然单位制，即忽略所有的 $c$ 或 $\hbar$。）

　　 由于 $A,B$ 两粒子体系的量子态是自旋单态，在对 $A$ 作测量时，根据正统量子力学，$B$ 粒子的状态 “似乎也发生了坍缩”。例如当 $A$ 粒子测得的 $S_z=1/2$ 时，$B$ 粒子测得的 $S_z$ 就一定是 $-1/2$，这是两电子的总自旋为 $0$ 的必然要求。那么，似乎有一种鬼魅般的超距作用在起作用。这是否符合我们对因果律的认知呢？是否真的存在某种非定域的超距作用？又似乎如同 EPR 论文中所说的那样存在某个正统量子力学的波函数之外的隐变量能够解释这一切？下面我们将先介绍 EPR 论文所基于的几个假设：定域论（Locality）和实在论。

1. 定域实在论假设

　　 EPR 佯谬是基于这样两个假设，来导出正统量子力学的不完备性的。这两个假设是：

1. 定域论：某区域发生的事件不能以超过光速的传递方式影响其它区域。对粒子 A 的测量不会影响到粒子 B 的状态。
2. 实在论：做实验观测到的现象是出自于某种物理实在，而这物理实在与观测无关。

　　 这里引出了一个概念：“物理实在”（Physical Reality）。它是指，在不对系统进行任何程度的扰动下，如果我们能准确预测物理量的值，那么就存在一个物理实在的元素与这个物理量对应。³

　　 以单粒子为例，它的坐标与动量算符是不对易的，因此我们无法同时精确测量它沿一个方向的坐标和动量，它们服从不确定性原理。这就意味着，沿一个方向的坐标和动量无法同时是物理实在。但是，如果我们有一个粒子，它具有确定的动量（我们仍未对它进行测量，但我们已经知道这一量子态具有该动量本征值），那么这一动量就是可被准确预测的，我们就称它为物理实在。注意物理实在不是指我们定义的那些变量或算符，而是代表那些我们能够准确预测的可测量的物理量，是一个物理上的概念。

　　 现在回到 Bell 实验。当我们对电子 A 测量得到 $S_z=1/2$ 的结果时，根据两电子处于一个自旋单态（总自旋为 $0$），我们就能够精准预测电子 B 的 $S_z$ 测量结果为 $-1/2$。这就意味着，在我们对 A 测量得到 $S_z=1/2$ 的结果时，B 电子的 $S_z$ 是一个物理实在。再根据定域论假设，对 A 的测量不可能通过超光速的作用影响 B 的状态，也就是说 B 电子的 $S_z$ 早已是物理实在，它自粒子源产生粒子源起就诞生了。

　　 注意我们除了能对电子 A 测量 $S_z$，还能测量 $S_x,S_y$。那么根据定域实在论，似乎对于 B 电子而言 $S_x,S_y,S_z$ 都是物理实在。这就造成了矛盾。电子三个方向自旋算符是两两不对易的。因此 EPR 佯谬最终导出一个结论：正统量子力学的波函数无法给出关于物理实在的完整描述。换句话说，正统量子力学是不完备的。除非我们推翻定域论或实在论这看似非常合理的假设。爱因斯坦和玻尔曾经围绕 EPR 佯谬展开辩论，辩论的焦点在论文中定域论和实在论的合理性。从现代的观点看，处于纠缠态的系统具有不可分割性，这种不可分割性是独立于空间的性质，因此局域性完全有可能违背。

2. 定域隐变量理论

　　 EPR 论文的最后给出了一个解决方案，他们认为存在一个完备的描述，即在波函数以外还存在一种隐变量，导致能够得到正统量子力学所预言的结果。这被称为是定域隐变量理论（Hidden-variable Theory）。可以看到，定域隐变量理论是基于定域实在论得到的理论，它蕴含着 Einstein 对 “上帝不掷骰子” 的物理学信仰。然而这一理论的数学必然是复杂的，我们对隐变量的结构一无所知。从而是否存在一个定域隐变量理论与正统量子力学等价，这件事是十分困难的。以至于自 EPR 佯谬提出以后，人们很长一段时间停滞在关于这个问题哲学和思辨层面的讨论。直到 1964 年 Bell 提出著名的 Bell 不等式，人们终于能够进行实验上定量的测量来检验两个理论孰是孰非。下面我们先对定域隐变量理论进行简要的介绍。

　　 我们知道，根据量子力学，假设 A 粒子和 B 粒子处于一个自旋单态（总自旋为 $0$。我们也可以取成其他的纠缠态。），那么对 A 粒子和 B 粒子的测量的统计结果是不独立的。我们用 $P(a | x)$ 表示经过测量 $x$ 得到结果 $a$ 的概率。$P(ab | xy)$ 表示，$A$ 粒子经过测量 $x$，$B$ 粒子经过测量 $y$ 后，分别得到结果 $a,b$ 的概率。那么有

我们希望引入一个隐变量 $\lambda$，它能够完备地给出物理实在的刻画。那么根据定域实在论的假设，当 $x,y,\lambda$ 确定后，$A$ 和 $B$ 粒子的测量结果将在统计上是独立的，这也意味着能够将它们分割成两个独立的互不干扰的系统。变量 $\lambda\in \Lambda$ 自粒子源产生两粒子的时候就被随机采样了，其采样的分布函数是 $q(\lambda)$，并且隐变量被 $A$ 和 $B$ 随身 “携带”。最后 $A$ 粒子的测量结果同时与 $x$ 和 $\lambda$ 有关，$B$ 粒子的测量结果同时与 $y$ 和 $\lambda$。我们有 然而隐变量无法被我们直接观测到，实验上能测量得到的统计结果是 $P(a|x),P(b|y),P(ab|xy)$。它们可以被表达为 以上就是定域隐变量理论的基本内容。

　　 1964 年 Bell 基于定域隐变量理论得到了 Bell 不等式。如果实验检验能够发现违背 Bell 不等式，则说明定域隐变量理论是错误的。1972 年，Freedman and Clauser 做了第一个贝尔检验（Bell test）⁴，结果违反 Bell 不等式。然而因为存在定域性漏洞，即纠缠的粒子间距离太小，不足以说明纠缠的非局域性，结果不具有说服力。随后，1982 年 Aspect, Grangier, and Roger 等人及后来更精密的实验观测都肯定正统量子力学理论是正确的，定域隐变量理论所给出的不等式与实验结果不符。

---

1. ^ 后来 Bohm 对这个思想实验进行了改进，使之具有更直观的物理图像，也就是我们现在看到的版本。
2. ^ 详见Stern-Gerlach 实验。
3. ^ 原文：If , without in any way disturbing to a system, we can predict with certainty the value of a physical quantity , then there exists an element of physical reality corresponding to this physical quantity.
4. ^ S.J. Freedman; J.F. Clauser (1972). "Experimental test of local hidden-variable theories".