Bell 不等式与 CHSH 不等式

                     

贡献者： _Eden_

　　 1964 年，Bell 给出了基于定域隐变量假定得出 Bell 不等式，从而把 EPR 佯谬所引发的一些思辨和哲学性的问题定量化和具体化，得到一个能够通过实验验证的判据。在这之后，1969 年 John Clauser，Michael Horne，Abner Shimony 和 Richard Holt 四人提出了 CHSH 不等式，使得 Bell 检验的实行更容易。由 CHSH 不等式也可以导出 Bell 不等式和所谓的 Bell 定理：即任何一个定域隐变量理论¹都无法复制量子力学的每一个结果。因此下面将直接给出 CHSH 不等式的证明。

1. Bell 实验与定域隐变量理论

　　 我们仍然以 Bohm 表述下的 Bell 实验为例，粒子源产生的两粒子 $A,B$ 处于自旋单态：

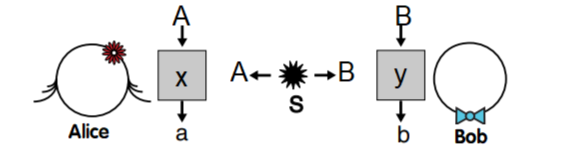
　　 假设 Alice 通过用测量方式 $x$ 得到粒子 $A$ 沿 $ \boldsymbol{\mathbf{n}} _x$ 方向的自旋。Bob 通过测量方式 $y$ 得到粒子 $B$ 沿 $ \boldsymbol{\mathbf{n}} _y$ 方向的自旋。假设 Alice 得到的测量结果为 $a$，Bob 得到的测量结果为 $b$。

　　 为了为了简化讨论，假设测量结果取值为 $\{-1,1\}$，因此相应的物理量测量算符可以表达为 $ \boldsymbol{\mathbf{\sigma}} \cdot \boldsymbol{\mathbf{n}} $（注意到自旋 $ \boldsymbol{\mathbf{S}} = \boldsymbol{\mathbf{\sigma}} /2$ 在各个方向上的本征值为 $\pm 1/2$）。

　　 回忆定域隐变量的基本假定：在粒子源产生两粒子时，$A,B$ 两粒子携带着隐变量 $\lambda$，它可能包含了粒子源产生两粒子时周围的一切环境因素和其他人们不知道和无法测量的信息。总之隐变量 $\lambda$ 在集合 $\Lambda$ 中以 $q(\lambda)$ 的概率分布函数被随机采样。我们有以下基本关系式：

其中 $P(a|x,\lambda)$ 代表由测量 $x$ 和隐变量 $\lambda$ 导致得到测量结果 $a$ 的概率。根据定域论，$A,B$ 两粒子的测量结果在统计上应当是独立的，即：

2. CHSH 不等式

　　 可以进行多次 Bell 实验，不改变测量方式 $x$ 或 $y$，再对结果进行统计，取其平均值，那么得到的结果就是数学期望值。例如 Alice 测得结果 $a$ 的期望就是：

上式是根据定域隐变量理论的基本假定得出的。根据正统量子力学的预言，结果 $a$ 的期望就是两粒子自旋单态的 $ \boldsymbol{\mathbf{\sigma}} _A\cdot \boldsymbol{\mathbf{n}} _x$ 算符期望值： 这是因为我们产生的自旋单态中某一个粒子沿任意方向的 $\pm 1$ 结果的概率应当是相等的，因而期望值就是 $0$。

　　 为了进一步研究两粒子自旋单态的纠缠性质，我们可以研究，当测量方式 $x,y$ 确定时，$a$ 与 $b$ 乘积的期望值：

其中我们定义了 $A(x,\lambda)=\sum_a aP(a|x,\lambda),B(x,\lambda)=\sum_b bP(b|y,\lambda)$。根据正统量子力学，对于一个自旋单态系统，上式是可以被精确计算的： 其中第二行运用了自旋单态的性质：$ \boldsymbol{\mathbf{\sigma}} _B \left\lvert \Psi^- \right\rangle =- \boldsymbol{\mathbf{\sigma}} _A \left\lvert \Psi^- \right\rangle $²。第三行用了泡利矩阵所满足的恒等式 $( \boldsymbol{\mathbf{\sigma}} \cdot \boldsymbol{\mathbf{x}} )( \boldsymbol{\mathbf{\sigma}} \cdot \boldsymbol{\mathbf{y}} )= \boldsymbol{\mathbf{x}} \cdot \boldsymbol{\mathbf{y}} +i \boldsymbol{\mathbf{\sigma}} \cdot ( \boldsymbol{\mathbf{x}} \times \boldsymbol{\mathbf{y}} )$。

　　 现在我们从式 6 出发，导出一些关系式。定域隐变量理论为了保护 “定域性” 而引入隐变量，实际上是一个很强的假定，相比于正统量子力学中对定域性的破坏，定域隐变量理论则是严格的遵守定域论的。这导致对纠缠态测量的统计结果很可能与正统量子力学相矛盾。让我们稍加推导：

注意到 $A(x,\lambda)=\sum_a a\cdot P(a|x,\lambda)$ 是 $x,\lambda$ 确定时 $a$ 的期望值，$a$ 的取值只有 $\pm 1$，因此有 $-1\le A\le 1$。类似地，$-1\le B\le 1$，$-1\le AB\le 1$。因此可以对式 8 的左右两侧取绝对值再进行放缩： 离 CHSH 不等式只差最后一步，可以去掉左侧绝对值，右侧 $\pm$ 取减号并移项，容易得到 这就是 CHSH 不等式。类似地，如果右侧 $\pm$ 取加号再移项，可以得到

　　 现在考虑一种特殊情况，即 $x'=y'=z$，那么 $\langle a(x')b(y')\rangle = - \boldsymbol{\mathbf{n}} _z\cdot \boldsymbol{\mathbf{n}} _z=-1$，代入式 9 将得到

这就是著名的 Bell 不等式。

3. CHSH 不等式的违反

　　 为了简便表达，将 $\langle a(x)b(y)\rangle$ 记作 $E(x,y)$。再次写下 CHSH 不等式：

根据正统量子力学的预测，$E(x,y)=- \boldsymbol{\mathbf{n}} _x\cdot \boldsymbol{\mathbf{n}} _y$。而事实上，如果我们取 我们将发现 CHSH 不等式的左侧为 $2\sqrt{2}$，这就违反了 CHSH 不等式，也证明了 Bell-定理：任何关于定域隐变量的理论都无法复制量子力学的每一个预测。

　　 因此如果在实验上我们能够制备出这样的纠缠态，并且能够检验它确确实实违反 Bell-CHSH 不等式，我们就能够证明定域隐变量的假设是错误的，正统量子力学才是正确的。1972 年，Freedman and Clauser 做了第一个贝尔检验³，违反了 Bell 不等式，但是该实验实际上存在定域性漏洞，两个分开的光子可能存在光速传递的 “作弊通信” 行为。1982 年 Aspect, Grangier, and Roger 等人及后来进行更精密的实验观测，对可能存在的漏洞进行了修复。如今，几乎所有的 Bell 实验都肯定正统量子力学理论是正确的，定域隐变量理论所给出的不等式与实验结果不符。

---

1. ^ 爱因斯坦等人于 EPR 佯谬的论文中提出的一个不同于正统量子力学的理论，基于定域实在论的假设，并假设一个完备的理论需要隐变量去刻画。
2. ^ 即 $ \left\lvert \Psi^- \right\rangle $ 是 $ \boldsymbol{\mathbf{S}} = \boldsymbol{\mathbf{S}} _A+ \boldsymbol{\mathbf{S}} _B$ 的本征值为 $0$ 的态。
3. ^ S.J. Freedman; J.F. Clauser (1972). "Experimental test of local hidden-variable theories".