贡献者: Giacomo; addis
1. 几何定义
我们先来看点乘的几何定义。注意该定义不需要任何坐标系的概念。
图 1:点乘的几何定义
两个几何向量的点乘(dot product),也叫点积、内积(inner product)或者标量积(scalar product)。如图 1 ,一般用一个实心圆点表示几何向量的点乘(不可省略)。点乘就是把两向量的模长相乘,再乘以它们的夹角1 $\theta$ 的余弦值:
\begin{equation}
\boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{B}} = \left\lvert \boldsymbol{\mathbf{A}} \right\rvert \left\lvert \boldsymbol{\mathbf{B}} \right\rvert \cos\theta ~,
\end{equation}
注意两个向量点乘得到的是一个标量(在这里就是实数)。几何定义中(
图 1 ),既可以把点乘理解为 $ \boldsymbol{\mathbf{A}} $ 投影在 $ \boldsymbol{\mathbf{B}} $ 上的模长乘以 $ \boldsymbol{\mathbf{B}} $ 的模长,也可以理解为 $ \boldsymbol{\mathbf{B}} $ 投影在 $ \boldsymbol{\mathbf{A}} $ 上的模长乘以 $ \boldsymbol{\mathbf{A}} $ 的模长。在这种理解下,若量向量的夹角为钝角,投影长度需要取负值。可见当两向量模长固定时,若方向相同,点乘结果取最大值 $ \left\lvert \boldsymbol{\mathbf{A}} \right\rvert \left\lvert \boldsymbol{\mathbf{B}} \right\rvert $;若方向相反,点乘取最小值 $- \left\lvert \boldsymbol{\mathbf{A}} \right\rvert \left\lvert \boldsymbol{\mathbf{B}} \right\rvert $;若相互垂直,则点乘为 0。
我们说两个点乘为 0 的向量互相垂直(perpendicular),或者说正交(orthogonal)。几何向量与自身点乘可得该向量模长的平方。单位向量与自己的点乘等于 1。
2. 坐标定义
若已知 $ \boldsymbol{\mathbf{A}} , \boldsymbol{\mathbf{B}} $ 在平面直角坐标系 $xy$ 中坐标分别为 $(A_x, A_y)$ 和 $(B_x, B_y)$,那么如何用坐标表示点乘运算的结果呢?我们把它定义为
\begin{equation}
\boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{B}} = A_x B_x + A_y B_y~.
\end{equation}
同理,空间向量点乘的坐标定义为
\begin{equation}
\boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{B}} = A_x B_x + A_y B_y + A_z B_z ~.
\end{equation}
可以想象,如果我们有 “更高维度的向量”,我们也可以直接用直角坐标定义点乘:
\begin{equation}
A_1 B_1 + \dots + A_n B_n ~.
\end{equation}
3. 两种定义的等价性
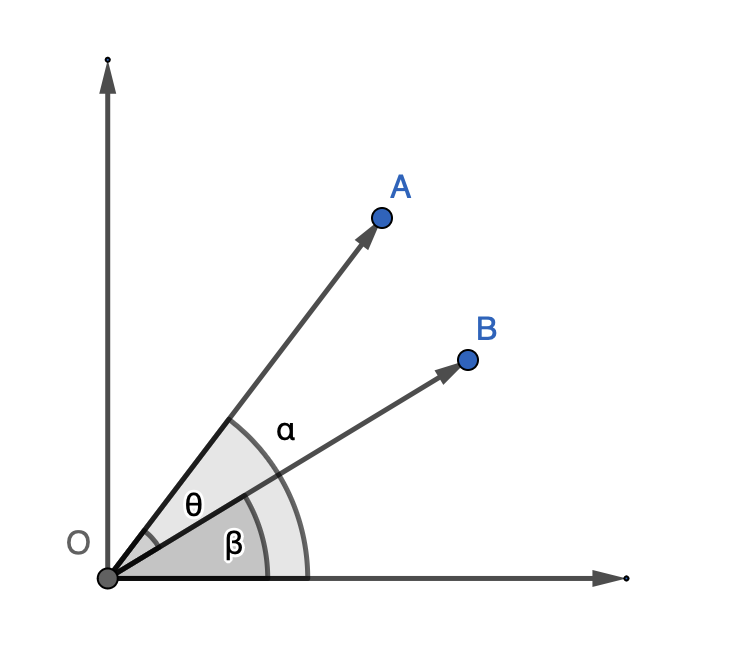
图 2
假设 $ \boldsymbol{\mathbf{A}} , \boldsymbol{\mathbf{B}} $ 处于第一象限,记 $ \boldsymbol{\mathbf{A}} $ 和 $ \hat{\boldsymbol{\mathbf{x}}} $ 的夹角为 $\alpha$,$ \boldsymbol{\mathbf{B}} $ 和 $ \hat{\boldsymbol{\mathbf{x}}} $ 的夹角为 $\beta$,$ \boldsymbol{\mathbf{A}} $ 和 $ \boldsymbol{\mathbf{B}} $ 的夹角为 $\theta$,如图 2 ,根据两角和公式(式 5 )有
\begin{equation}
\cos\theta = \cos\left(\alpha-\beta\right) = \cos\alpha \cos\beta + \sin\alpha \sin\beta~,
\end{equation}
因此
\begin{equation}
\begin{aligned}
| \boldsymbol{\mathbf{A}} | | \boldsymbol{\mathbf{B}} | \cos\theta &= | \boldsymbol{\mathbf{A}} | \cos\alpha | \boldsymbol{\mathbf{B}} | \cos\beta + | \boldsymbol{\mathbf{A}} | \sin\alpha | \boldsymbol{\mathbf{B}} | \sin\beta \\
&= A_x B_x + A_y B_y
\end{aligned}~
\end{equation}
对于空间向量也是一样的。
4. 点乘的性质
点乘满足交换率:
\begin{equation}
\boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{B}} = \boldsymbol{\mathbf{B}} \boldsymbol\cdot \boldsymbol{\mathbf{A}} ~.
\end{equation}
由几何定义,易证。
点乘满足分配律:
\begin{equation}
\boldsymbol{\mathbf{A}} \boldsymbol\cdot ( \boldsymbol{\mathbf{B}} + \boldsymbol{\mathbf{C}} ) = \boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{B}} + \boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{C}} ~,
\end{equation}
考虑坐标定义,我们有
\begin{equation}
\begin{aligned}
\boldsymbol{\mathbf{A}} \boldsymbol\cdot ( \boldsymbol{\mathbf{B}} + \boldsymbol{\mathbf{C}} ) &= A_1 (B_1 + C_1) + A_2 (B_2 + C_2) \\
&= A_1 B_1 + A_1 C_1 + A_2 B_2 + A_2 C_2 \\
&= (A_1 B_1 + A_2 B_2) + (A_1 C_1 + A_2 C_2) \\
&= \boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{B}} + \boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{C}}
\end{aligned}~
\end{equation}
空间向量的证明类似。
注意点乘不满足结合律,即
\begin{equation}
( \boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{B}} ) \boldsymbol{\mathbf{C}} \ne \boldsymbol{\mathbf{A}} ( \boldsymbol{\mathbf{B}} \boldsymbol\cdot \boldsymbol{\mathbf{C}} )~.
\end{equation}
前者是 $ \boldsymbol{\mathbf{C}} $ 方向的向量,后者是 $ \boldsymbol{\mathbf{A}} $ 方向的向量,显然不一定相等。
5. 证明点乘的分配律
图 3:点乘分配律的证明
如图 3 ,令 $ \boldsymbol{\mathbf{D}} \equiv \boldsymbol{\mathbf{B}} + \boldsymbol{\mathbf{C}} $,把 $ \boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{B}} $, $ \boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{C}} $, $ \boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{D}} $ 分别用几何定义理解为 $ \boldsymbol{\mathbf{B}} $, $ \boldsymbol{\mathbf{C}} $, $ \boldsymbol{\mathbf{D}} $ 在 $ \boldsymbol{\mathbf{A}} $ 上的投影乘 $ \left\lvert \boldsymbol{\mathbf{A}} \right\rvert $,且令投影长度分别为 $L_B, L_C, L_D$。那么要证明 $ \boldsymbol{\mathbf{A}} \boldsymbol\cdot ( \boldsymbol{\mathbf{B}} + \boldsymbol{\mathbf{C}} ) = \boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{D}} = \boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{B}} + \boldsymbol{\mathbf{A}} \boldsymbol\cdot \boldsymbol{\mathbf{C}} $,只需证明 $L_D = L_B + L_C$ 即可。现在把 $ \boldsymbol{\mathbf{B}} $ 平移使其起点与 $ \boldsymbol{\mathbf{C}} $ 的终点对接(投影长度不变)。从图中立即得出 $L_D = L_B + L_C$。
1. ^ 对于空间向量来说,我们需要先截取这两个向量所在的平面(如果它们不平行则平面唯一确定)。
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。