电偶极子辐射

贡献者： ACertainUser; addis

本文处于草稿阶段。

预备知识　电磁场推迟势

　　¹令原点处的电偶极子为

\begin{equation} \boldsymbol{\mathbf{p}} (t) = p_0 \cos\left(\omega t\right) \hat{\boldsymbol{\mathbf{z}}} ~. \end{equation}

　　使用洛伦兹规范，在 $d \ll \lambda \ll r$ 的远场近似下（$d$ 是偶极子的长度，$\lambda = \frac{2\pi}{k}$）

\begin{equation} \varphi(r, \theta, t) = -\frac{p_0\omega}{4\pi\epsilon_0 c} \left(\frac{\cos\theta}{r} \right) \sin[\omega(t - r/c)]~, \end{equation}

\begin{equation} \boldsymbol{\mathbf{A}} (r, \theta, t) = -\frac{\mu_0 p_0 \omega}{4\pi r} \sin[\omega(t - r/c)] \hat{\boldsymbol{\mathbf{z}}} ~. \end{equation}

进而得

\begin{equation} \boldsymbol{\mathbf{E}} = -\frac{\mu_0 p_0\omega^2}{4\pi} \left(\frac{\sin\theta}{r} \right) \cos[\omega(t - r/c)] \hat{\boldsymbol{\mathbf{\theta}}} ~~, \end{equation}

\begin{equation} \boldsymbol{\mathbf{B}} = -\frac{\mu_0 p_0\omega^2}{4\pi c} \left(\frac{\sin\theta}{r} \right) \cos[\omega(t - r/c)] \hat{\boldsymbol{\mathbf{\phi}}} ~. \end{equation}

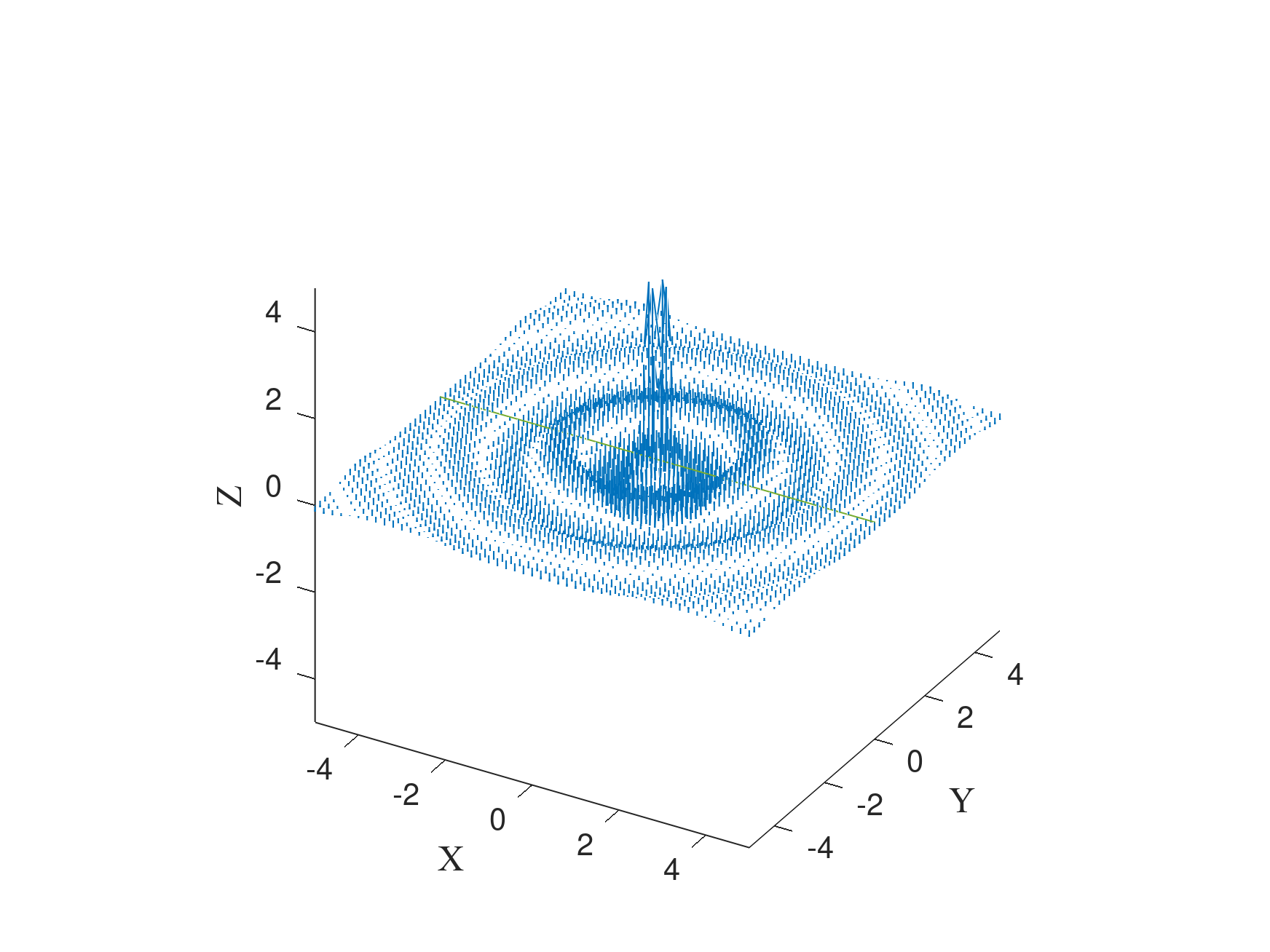
图 1：$Z=0$ 平面上的电场矢量场.原点附近由于远场近似不再有效而发散。笔者制作的一个可动的立体模型（站外链接）

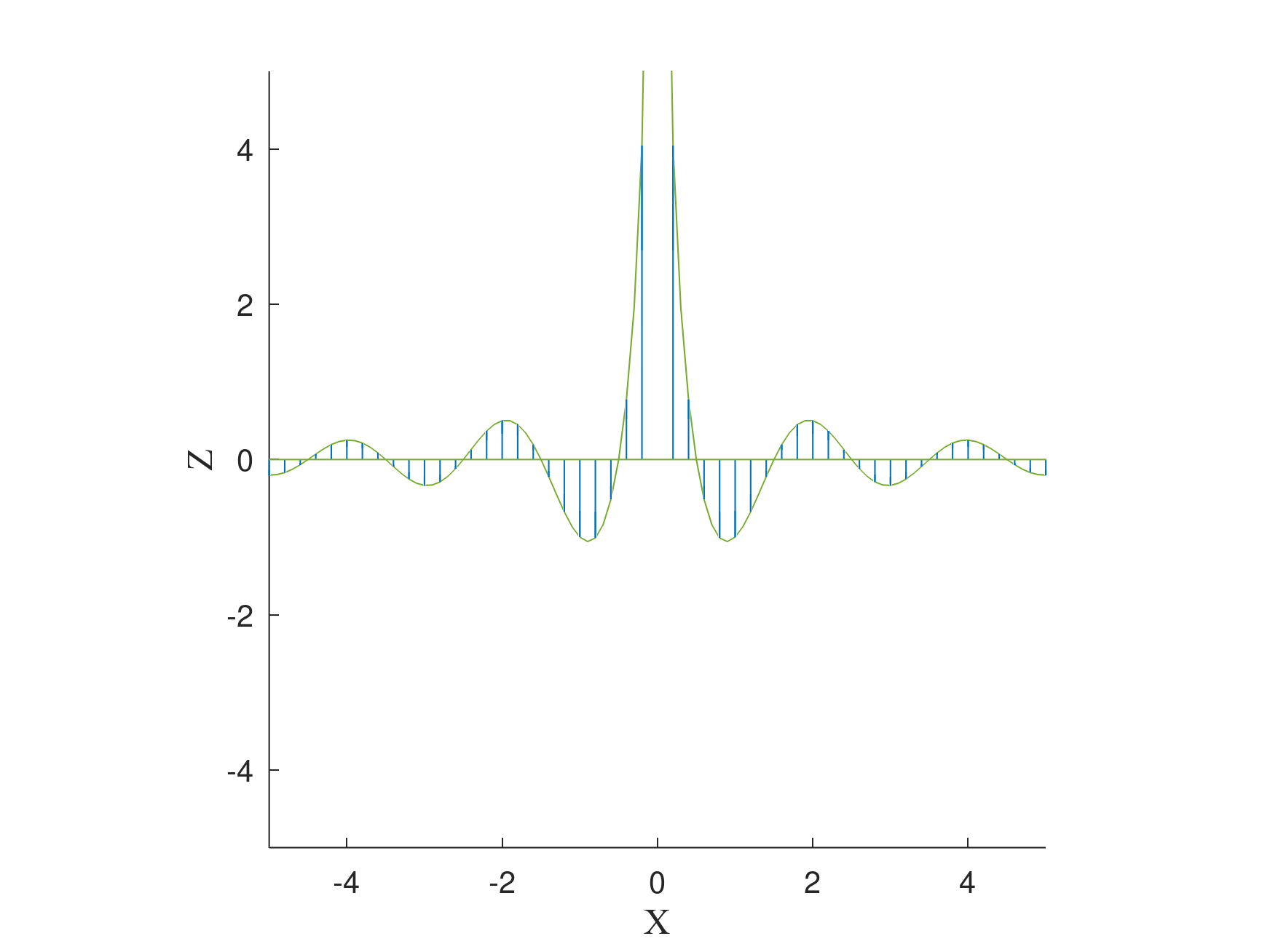
图 2：$X$ 轴上的电场矢量场。在远处辐射场行为类似平面电磁波

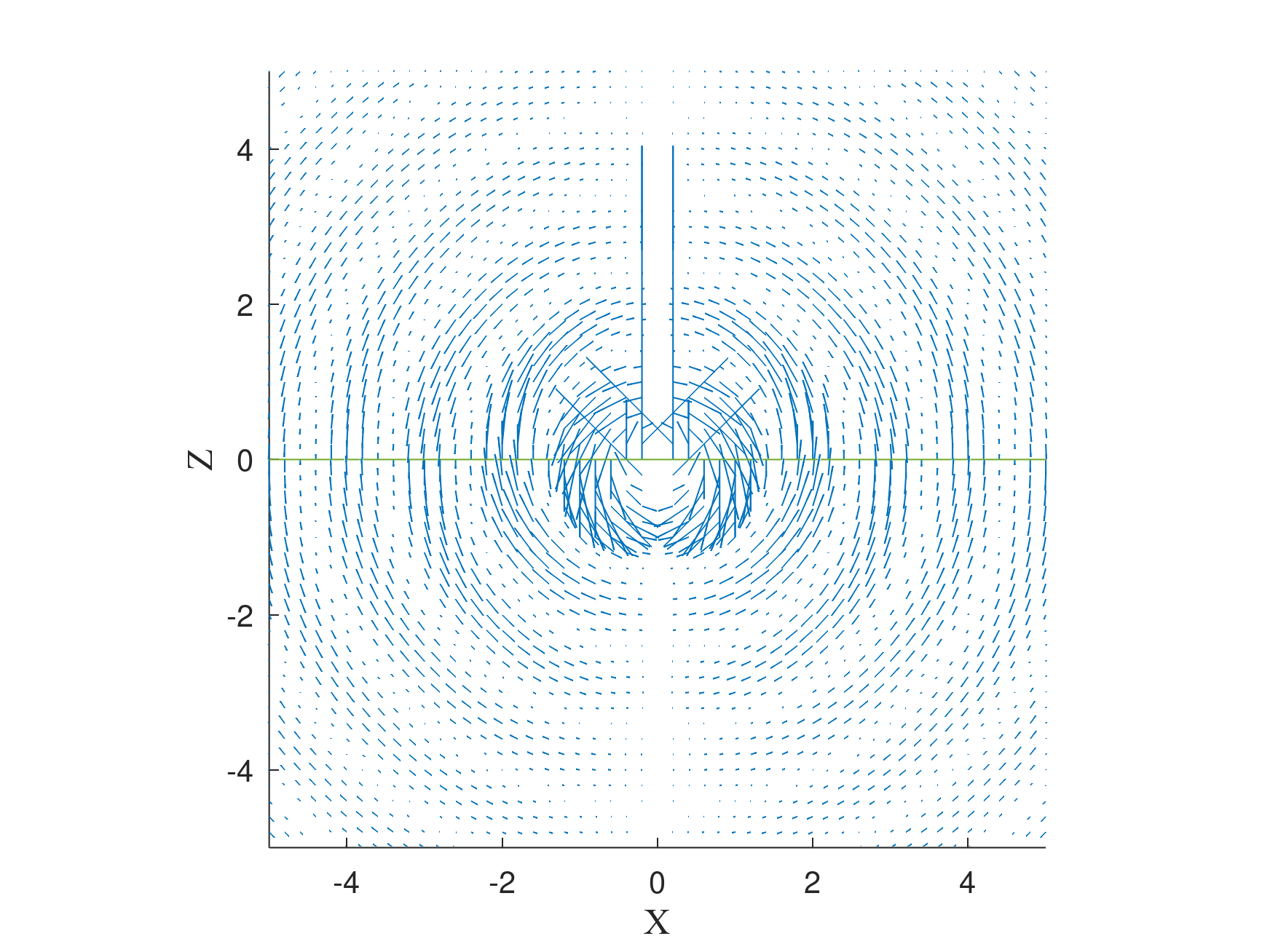
图 3：$Y=0$ 上的电场矢量场。

绘制矢量场的.m 代码

clc
clear
T=2;%周期
w=2*pi/T;
v=1;%波速
k=w/v;
t=0;%时刻

[x y z] = meshgrid(-5:0.2:5,-5:0.2:5,-5:0.2:5);
%将轴的范围设成0，可得到截面上的矢量场.完整的矢量场太复杂了
[phi theta r]=cart2sph(x,y,z);
theta = pi/2-theta;
E = -(sin(theta)./r).*cos(w*t-k*r);%电场强度数值
a = E.*cos(theta).*cos(phi);
b = E.*cos(theta).*sin(phi);
c = E.*-sin(theta);

hold on
axis equal;
axis([-5 5 -5 5 -5 5]);

xlabel('X','fontsize',12,'fontname','Times New Roman');
ylabel('Y','fontsize',12,'fontname','Times New Roman');
zlabel('Z','fontsize',12,'fontname','Times New Roman');

quiver3(x,y,z,a,b,c,0);

line([-10 10], [0 0],[0 0]);

hold off

辐射功率

　　可用能流密度（坡印廷矢量）描述辐射功率。

\begin{equation} \boldsymbol{\mathbf{s}} ( \boldsymbol{\mathbf{r}} , t) = \frac{1}{\mu_0} \boldsymbol{\mathbf{E}} \boldsymbol\times \boldsymbol{\mathbf{B}} = \frac{\mu_0p_0^2\omega^4}{16\pi^2c} \frac{\sin^2\theta}{r^2} \cos^2[\omega(t - r/c)] \hat{\boldsymbol{\mathbf{r}}} ~. \end{equation}

时间平均值为

\begin{equation} \left\langle \boldsymbol{\mathbf{s}} \right\rangle = \frac{1}{\mu_0} \boldsymbol{\mathbf{E}} \boldsymbol\times \boldsymbol{\mathbf{B}} = \frac{\mu_0p_0^2\omega^4}{32\pi^2c} \frac{\sin^2\theta}{r^2} \hat{\boldsymbol{\mathbf{r}}} ~. \end{equation}

图 4：$ \left\langle \boldsymbol{\mathbf{s}} \right\rangle $ 的“等强度面”,内圈的 $ \left\langle \boldsymbol{\mathbf{s}} \right\rangle $ 强度更高.注意平行于偶极子的方向上没有能流.一个立体模型（站外链接）

　　总辐射功率（时间平均）为

\begin{equation} \left\langle P \right\rangle = \oint \left\langle \boldsymbol{\mathbf{s}} \right\rangle \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{a}} } = \frac{\mu_0 p_0^2 \omega^4}{12\pi c}~. \end{equation}

总辐射功率是定值体现了能量守恒。如果总辐射功率不为定值，说明来自源的一部分能量在传播过程中被损耗掉了。

1. ^ 参考 [1]。

[1] ^ David Griffiths, Introduction to Electrodynamics, 4ed

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。