布洛赫理论
贡献者： Zona; addis; _Eden_
在固体物理中，我们研究原子按一定规则排布而成的理想晶格，研究电子在一个具有晶格周期性的等效势场 $V( \boldsymbol{\mathbf{r}} )$ 中的运动。根据定态薛定谔方程，我们有
\begin{equation}
H\psi= \left[-\frac{\hbar^2}{2m}\nabla^2+V( \boldsymbol{\mathbf{r}} ) \right] \psi = E\psi~,
\end{equation}
\begin{equation}
V( \boldsymbol{\mathbf{r}} )=V( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} _n)~,
\end{equation}
为了研究周期性势场下定态薛定谔方程的解，我们可以从最简单的一维薛定谔方程出发。
1. Bloch theory
1布洛赫（Bloch）理论也叫 Floquet 理论，是由对称性得到的严格结论。它的内容可以表述如下：
也就是说，将空间坐标 $ \boldsymbol{\mathbf{r}} $ 平移格矢 $ \boldsymbol{\mathbf{R}} $，平移前后的波函数只相差一个跟 $ \boldsymbol{\mathbf{R}} $ 有关的相位因子，不改变波函数本身的物理性质。
$\psi ( \boldsymbol{\mathbf{r}} )$ 称为布洛赫函数（Bloch function），晶体中用布洛赫函数来描述的电子称为布洛赫电子，与真空中的自由电子区分。
布洛赫定理的另一种等价描述为：
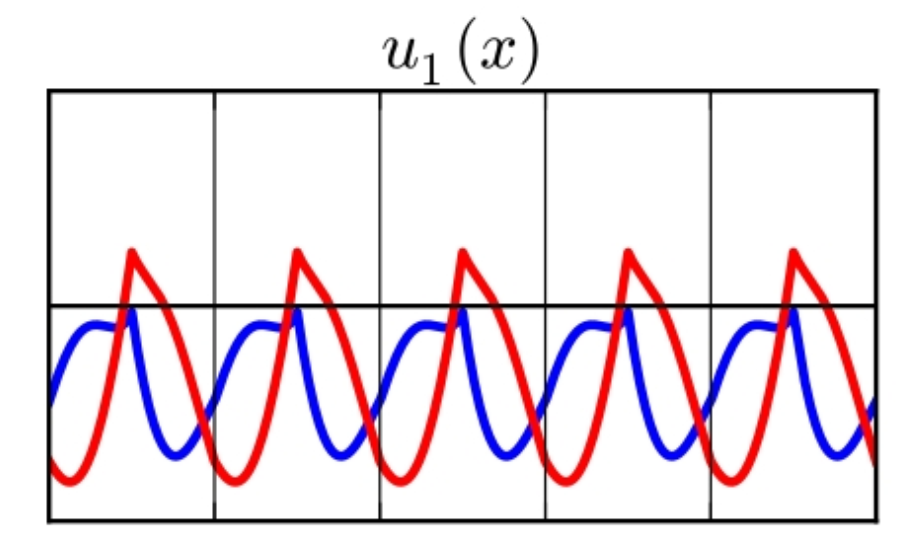
从 Bloch 定理的等价描述中，我们可以初步看到，布洛赫函数是真空中自由电子的平面波受到周期性势场的调制的结果。
图 1：周期函数 $u_1$，蓝线为实部，红线为虚部。
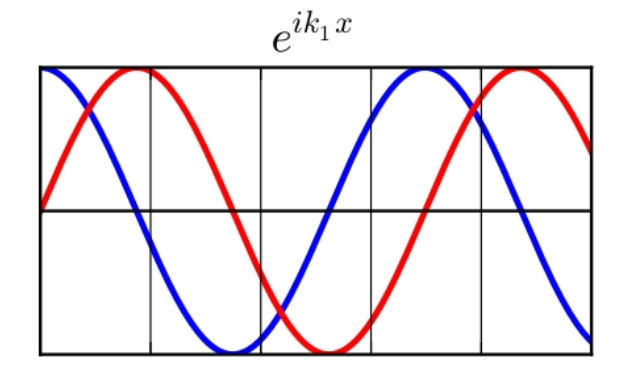
图 2：一维平面波 $ \mathrm{e} ^{ \mathrm{i} k_1 x}$
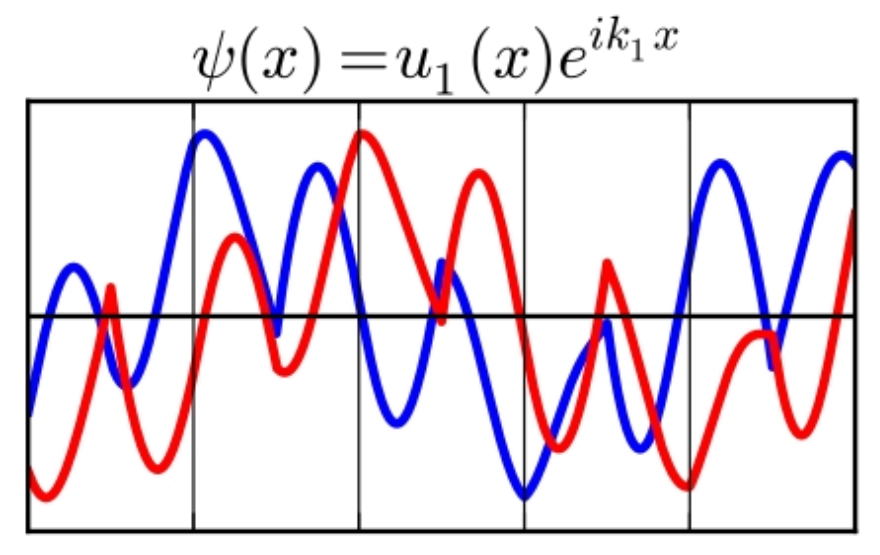
图 3：一维布洛赫函数 $\psi(x)$
由式 3 到式 4 ，等式两边同乘 $ \mathrm{e} ^{- \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot ( \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{r}} )}$:
\begin{equation}
\mathrm{e} ^{- \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot ( \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{r}} )}\psi( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} ) = \mathrm{e} ^{- \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} }\psi( \boldsymbol{\mathbf{r}} )~,
\end{equation}
\begin{equation}
u( \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{r}} ) = u( \boldsymbol{\mathbf{r}} ),~\quad u( \boldsymbol{\mathbf{r}} ) = \mathrm{e} ^{- \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} }\psi( \boldsymbol{\mathbf{r}} )~.
\end{equation}
\begin{equation}
\psi( \boldsymbol{\mathbf{r}} ) = \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} } u( \boldsymbol{\mathbf{r}} )~.
\end{equation}
\begin{align}
\psi( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} ) &= \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot ( \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{r}} )} u( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} )\\
&= \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{R}} } \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} }u( \boldsymbol{\mathbf{r}} )\\ &= \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{R}} } \psi( \boldsymbol{\mathbf{r}} )~.
\end{align}
布洛赫定理的量子力学证明
上面我们从数学角度出发，仅利用了函数的周期性性质。下面用量子力学的语言证明 Bloch 定理，即周期性空间平移的效果仅是给波函数添加 phase shift, 不改变物理实质。
定义平移算符 $\hat{T}_{ \boldsymbol{\mathbf{R}} }$，将 $\hat{T}_{ \boldsymbol{\mathbf{R}} }$ 作用到任何函数 $f( \boldsymbol{\mathbf{r}} )$ 上的作用是：
\begin{equation}
\hat{T}_{ \boldsymbol{\mathbf{R}} } f( \boldsymbol{\mathbf{r}} ) = f( \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{r}} )~,
\end{equation}
\begin{equation}
\hat{T}_{ \boldsymbol{\mathbf{R}} '}\hat{T}_{ \boldsymbol{\mathbf{R}} } f( \boldsymbol{\mathbf{r}} ) = \hat{T}_{ \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{R}} '}f( \boldsymbol{\mathbf{r}} )~.
\end{equation}
从物理直觉上，晶体的周期性势场使得周期性平移不改变电子所处的晶格系统的哈密顿量，也即能量守恒。下面将从数学角度证明哈密顿量与平移算符的对易性。
\begin{equation}
\begin{aligned}
\hat{T}_{ \boldsymbol{\mathbf{R}} } \hat{H} f( \boldsymbol{\mathbf{r}} ) &= \hat{T}_{ \boldsymbol{\mathbf{R}} } \left[ \left(-\frac{\hbar^2}{2m}\nabla^2+V( \boldsymbol{\mathbf{r}} ) \right) f( \boldsymbol{\mathbf{r}} ) \right] \\
&= \left[-\frac{\hbar^2}{2m}\nabla^2+V( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} ) \right] f( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} )\\
&= \left[-\frac{\hbar^2}{2m}\nabla^2+V( \boldsymbol{\mathbf{r}} ) \right] f( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} )\\
& = \hat{H} \hat{T}_{ \boldsymbol{\mathbf{R}} } f( \boldsymbol{\mathbf{r}} )~.
\end{aligned}
\end{equation}
写成对易算符形式，也即
\begin{equation}
[\hat{T},\hat{H}] = 0~.
\end{equation}
设哈密顿量的本征态为 $\psi$，由算符对易性可知，$\psi$ 也是算符 $\hat{T}$ 的本征态：
\begin{equation}
\hat{T}_{ \boldsymbol{\mathbf{R}} } \psi ( \boldsymbol{\mathbf{r}} ) = \lambda_{ \boldsymbol{\mathbf{R}} }\psi =\psi( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} )~,
\end{equation}
\begin{equation}
\hat{T}_{ \boldsymbol{\mathbf{R}} '} \hat{T}_{ \boldsymbol{\mathbf{R}} }\psi ( \boldsymbol{\mathbf{r}} ) = \lambda_{ \boldsymbol{\mathbf{R}} '}\lambda_{ \boldsymbol{\mathbf{R}} }\psi ( \boldsymbol{\mathbf{r}} ) = \lambda_{ \boldsymbol{\mathbf{R}} ' + \boldsymbol{\mathbf{R}} } \psi ( \boldsymbol{\mathbf{r}} )~,
\end{equation}
\begin{equation}
\lambda_{ \boldsymbol{\mathbf{R}} '}\lambda_{ \boldsymbol{\mathbf{R}} } = \lambda_{ \boldsymbol{\mathbf{R}} ' + \boldsymbol{\mathbf{R}} }~,
\end{equation}
\begin{equation}
\mathrm{e} ^{ \mathrm{i} (\beta_{ \boldsymbol{\mathbf{R}} '}+ \beta_{ \boldsymbol{\mathbf{R}} })} = \mathrm{e} ^{ \mathrm{i} \beta_{ \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{R}} '}}~,
\end{equation}
\begin{equation}
\lambda_{ \boldsymbol{\mathbf{R}} } = \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{R}} }~,
\end{equation}
也许初入量子力学的读者会对这些算符操作产生困惑，因为从表面上看起来，它们和物理实质并不挂钩，依然仅是一通数学操作。但我们要明白，算符操作实际上是将物理意义映射在线性代数空间下的数学操作，看起来抽象的数学，本质上依然是在为物理服务。每一步操作下，都有它们对应的物理含义。
物理意义
不同原胞内的电子具有相同的密度分布：
\begin{equation}
|\psi( \boldsymbol{\mathbf{r}} )|^2 = |u( \boldsymbol{\mathbf{r}} )|^2 = |\psi( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} )|^2~,
\end{equation}
图 4：晶体中的周期性势场
2. 波矢 $ \boldsymbol{\mathbf{k}} $ 的物理意义
从上述量子力学的推导过程中我们可以看到，本质上 $ \boldsymbol{\mathbf{k}} $ 来源于平移算符的本征值：
\begin{equation}
\hat{T}_{ \boldsymbol{\mathbf{R}} } \psi ( \boldsymbol{\mathbf{r}} ) = \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{R}} }\psi ( \boldsymbol{\mathbf{r}} )~,
\end{equation}
那 $\hbar \boldsymbol{\mathbf{k}} $ 又代表什么呢？乍一看像是电子的动量。且慢，让我们仔细算算动量算符 $\hat{p}$ 的本征值：
\begin{equation}
\begin{aligned}
\hat{p} \psi_{ \boldsymbol{\mathbf{k}} } ( \boldsymbol{\mathbf{r}} ) &= - \mathrm{i} \hbar \dfrac{\partial}{\partial \boldsymbol{\mathbf{r}} } \left( \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} } u( \boldsymbol{\mathbf{r}} ) \right) \\
& = \hbar \boldsymbol{\mathbf{k}} \psi_{ \boldsymbol{\mathbf{k}} } ( \boldsymbol{\mathbf{r}} ) - \mathrm{i} \hbar \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} } \dfrac{\partial u( \boldsymbol{\mathbf{r}} )}{\partial \boldsymbol{\mathbf{r}} }\\
&\neq \hbar \boldsymbol{\mathbf{k}} \psi_{ \boldsymbol{\mathbf{k}} } ( \boldsymbol{\mathbf{r}} )\\~.
\end{aligned}
\end{equation}
$ \boldsymbol{\mathbf{k}} $ 可以取任意值吗？从直觉上这是不可能的，一方面无限大动能的电子不存在，另一方面如果电子动能很大，它早就跑出晶体了。所以我们需要考虑 $ \boldsymbol{\mathbf{k}} $ 满足的限制条件：周期平移不变性。实际晶体不是无穷大的，周期性平移电子总会跑出晶体之外，这该怎么办？物理学家常用的处理方法是将其 “绕回去”，引入周期性边界条件：设晶格在三个方向上的原胞数量分别为 $N_1,N_2,N_3$，则平移 $N_1$ 个原胞后得到的波函数与初态相同，又回去了：
\begin{equation}
\hat T _{N_1 \boldsymbol{\mathbf{a}} _1}\psi_{ \boldsymbol{\mathbf{k}} }( \boldsymbol{\mathbf{r}} )=\psi_{ \boldsymbol{\mathbf{k}} }( \boldsymbol{\mathbf{r}} +N_1 \boldsymbol{\mathbf{a}} _1) = \psi_{ \boldsymbol{\mathbf{k}} }( \boldsymbol{\mathbf{r}} )~,
\end{equation}
\begin{equation}
e^{ \mathrm{i} N_1 \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{a}} _1} = 1,~ k_1 =\frac{2\pi m_1}{N_1}~.
\end{equation}
\begin{equation}
\boldsymbol{\mathbf{k}} = \dfrac{m_1}{N_1 a_1} \boldsymbol{\mathbf{b}} _1 + \dfrac{m_2}{N_2 a_2} \boldsymbol{\mathbf{b}} _2 + \dfrac{m_3}{N_3 a_3} \boldsymbol{\mathbf{b}} _3,~ m_1,m_2,m_3 \in \mathbb{Z}~.
\end{equation}
图 5：由原胞组成的晶体
未完成：增加倒格基矢、倒格空间等相关的文章
3. 一维布洛赫函数
在一维情况下，波函数可以记为
\begin{equation}
\psi(x) = e^{ \mathrm{i} K x} u(x)~,
\end{equation}
如果我们施加循环边界条件（$N$ 是晶体一个方向的原子数，阿伏伽德罗常数数量级）
\begin{equation}
\psi(x+Na) = \psi(x)~,
\end{equation}
\begin{equation}
K = \frac{2\pi}{a} \frac{n}{N} \qquad (n \in \mathbb Z)~,
\end{equation}
一个例子见一维 delta 势能晶格。
4. 三维布洛赫函数
\begin{equation}
\phi( \boldsymbol{\mathbf{r}} ) = \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} } u( \boldsymbol{\mathbf{r}} )~,
\end{equation}
\begin{equation}
u( \boldsymbol{\mathbf{r}} )=u( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} _n)~,
\end{equation}
\begin{equation}
T_\alpha u( \boldsymbol{\mathbf{r}} )= u( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{a}} _\alpha),\alpha=1,2,3~,
\end{equation}
\begin{equation}
\begin{aligned}
&H\psi=E\psi,\\
&T_\alpha \psi = \lambda_\alpha \psi, \alpha=1,2,3~.
\end{aligned}
\end{equation}
\begin{equation}
\psi( \boldsymbol{\mathbf{r}} )=\psi( \boldsymbol{\mathbf{r}} +N_\alpha \boldsymbol{\mathbf{a}} _\alpha),\alpha=1,2,3~
\end{equation}
\begin{equation}
\lambda_\alpha=e^{ \dfrac{2\pi i l_\alpha}{N_\alpha}}~,
\end{equation}
如果引入倒格子矢量 $ \boldsymbol{\mathbf{b}} _1, \boldsymbol{\mathbf{b}} _2, \boldsymbol{\mathbf{b}} _3$，满足 $ \boldsymbol{\mathbf{a}} _i \boldsymbol\cdot \boldsymbol{\mathbf{b}} _j = 2\pi \delta_{ij}$，那么
\begin{equation}
\begin{aligned}
&\lambda_\alpha = e^{i \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{a}} _\alpha}\\
& \boldsymbol{\mathbf{k}} =\sum_\alpha\frac{l_\alpha}{N_\alpha} \boldsymbol{\mathbf{b}} _\alpha~.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\psi \left( \boldsymbol{\mathbf{r}} +\sum_\alpha m_\alpha \boldsymbol{\mathbf{a}} _\alpha \right) &= T_1^{m_1} T_2^{m_2} T_3^{m_3} \psi( \boldsymbol{\mathbf{r}} )\\
&=e^{i \boldsymbol{\mathbf{k}} \boldsymbol\cdot \left(\sum_\alpha m_\alpha \boldsymbol{\mathbf{a}} _\alpha \right) }\psi( \boldsymbol{\mathbf{r}} )~.
\end{aligned}
\end{equation}
[1] ^ 黄昆. 固体物理学 高等教育出版社
[2] ^ Bransden, Physics of Atoms and Molecules, 2ed
[3] ^ David Griffiths, Introduction to Quantum Mechanics, 4ed
致读者： 小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此，我们请求广大读者热心打赏 ，使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损， 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款， 他们的付出帮助了 99% 的读者免费获取知识， 我们在此表示感谢。
友情链接： 超理论坛 | ©小时科技 保留一切权利