贡献者: 待更新
如果我们要测量线偏振的超快激光脉冲的波形(即电场关于时间的函数),我们不能直接用仪器测量,因为电子元件的时间分辨率远远不够。但我们可以使用 Frequency Resolved Optical Gating(FROG)。FROG 有许多不同的实现方法,这里只讨论比较常见的 SHG FROG(Second Harmonic Generation FROG)和 PCGPA。
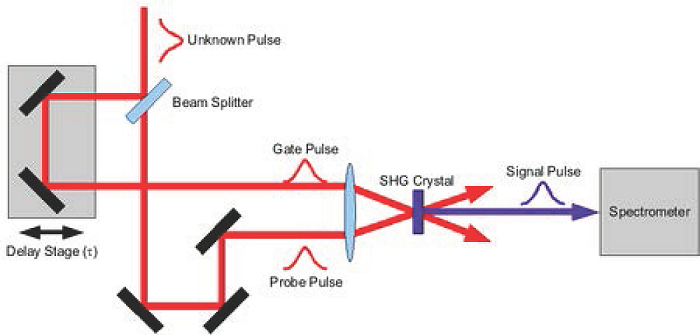
图 1:SHG FROG 的光路(图片来自 WikiPedia)
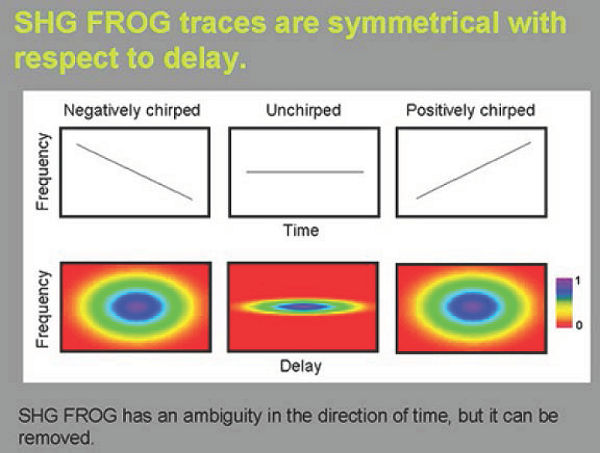
图 2:SHG FROG trace(图片来自网络)
Frog 的大概原理就是把被测量的脉冲(prob)$f(t)$ 和另一个脉冲(gate)$g(t)$ 叠加(注意 $f(t)$ 和 $g(t)$ 都是实函数),然后通过一个二阶非线性介质产生一个 $f(t)g(t)$ 脉冲并分离出来,再测量光谱(即傅里叶变换)。接下来我们可以控制两个脉冲的相对延迟(time delay)$\tau$,就得到不同延迟下 $f(t - \tau)g(t)$ 的光谱,也就是一个二维函数,叫做 FROG trace(图 2 )。很多情况下,gate 就是 prob 通过一个 beam splitter 分出来的,实验光路如图 1 所示。
\begin{equation}
a(\omega, \tau) = \left\lvert \int_{-\infty}^{\infty} f(t-\tau) g(t) \mathrm{e} ^{- \mathrm{i} \omega t} \,\mathrm{d}{t} \right\rvert ^2~.
\end{equation}
只要用特定的算法,就可以从
式 1 中解出 $f(t)$ 和 $g(t)$。
1. PCGPA 算法
PCGPA(Principal Component General Projection Algorithm)就是从式 1 中解出 $f(t)$ 和 $g(t)$ 的一种常见算法。在得到 我们假设 $f(t)$ 和 $g(t)$ 都是等时间间隔的离散点 $f_1, f_2\dots, f_N$ 和 $g_2, g_2\dots, g_N$,可以看成两个列矢量。我们先来做两矢量的外积,即
\begin{equation}
\boldsymbol{\mathbf{f}} \boldsymbol{\mathbf{g}} ^{\mathrm{T}} = \begin{pmatrix}
f_1g_1 & \ldots & f_1g_N\\
\vdots & \ddots & \vdots\\
f_Ng_1 & \ldots & f_Ng_N\end{pmatrix} ~.
\end{equation}
然后我们把第 $i$ 行向左移动 $i-1$ 个元(左边多出的矩阵元补到右边),得到
\begin{equation}
\begin{pmatrix}
f_1g_1 & f_1g_2 & \ldots & f_1g_N\\
f_2g_2 & f_2g_3 & \ldots & f_2g_1\\
\vdots & \vdots & \vdots & \vdots\\
f_Ng_N & f_Ng_1 & \ldots & f_Ng_{N-1}
\end{pmatrix} ~.\end{equation}
现在可以发现每一列恰好是 $f(t-\tau)g(t)$ 的离散形式
1,第 $i$ 列 $\tau = (i - 1)\Delta t$。然而当 $i > N/2$ 的时候,更自然的理解是 $\tau = (i-N)\Delta t$。例如与其认为第 $N$ 列是 $g$ 向上移动了 $N-1$ 个元,倒不如认为是向下移动了 $1$ 个元。根据这种思想,我们可以把矩阵左半和右半调换得到
\begin{equation}
\begin{pmatrix}
f_1g_{N/2 + 1} & f_1g_{N/2+2} & \ldots & f_1g_{N/2}\\
f_2g_{N/2 + 2} & f_2g_{N/2+3} & \ldots & f_2g_{N/2+1}\\
\vdots & \vdots & \vdots & \vdots\\
f_Ng_{N/2} & f_Ng_{N/2+1} & \ldots & f_Ng_{N/2-1}
\end{pmatrix} ~.\end{equation}
这样,从左到右的每列分别对应从 $\tau = -(N/2)\Delta t, \dots, (N/2 - 1)\Delta t$。
现在我们对每一列做离散傅里叶变换(注意前后都要 fftshift),就得到了含相位的 Frog trace 矩阵,其中的每一列都是式 1 中的
\begin{equation}
\int_{-\infty}^{\infty} f(t-\tau) g(t) \mathrm{e} ^{- \mathrm{i} \omega t} \,\mathrm{d}{t} ~.
\end{equation}
1. ^ 唯一的区别是从最上面移出的 $g_i$ 跑到了最下面,而在实验中最下面应该由 0 来填补。但如果 $ \boldsymbol{\mathbf{f}} $ 和 $ \boldsymbol{\mathbf{g}} $ 矢量的首尾都有足够多的 0,这个问题就自动解决了。
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。