无限深势阱中的高斯波包模拟(Matlab)
贡献者: addis
本文中我们来计算无限深势阱中一个高斯波包的运动。定性来说,波包会一边移动一边扩散(变宽变矮),且在两个势阱壁之间来回反弹。反弹的过程中会发生干涉。
图 1:束缚态概率分布,$x$ 轴为束缚态的 $n$,$y$ 轴为概率,求和约等于 1
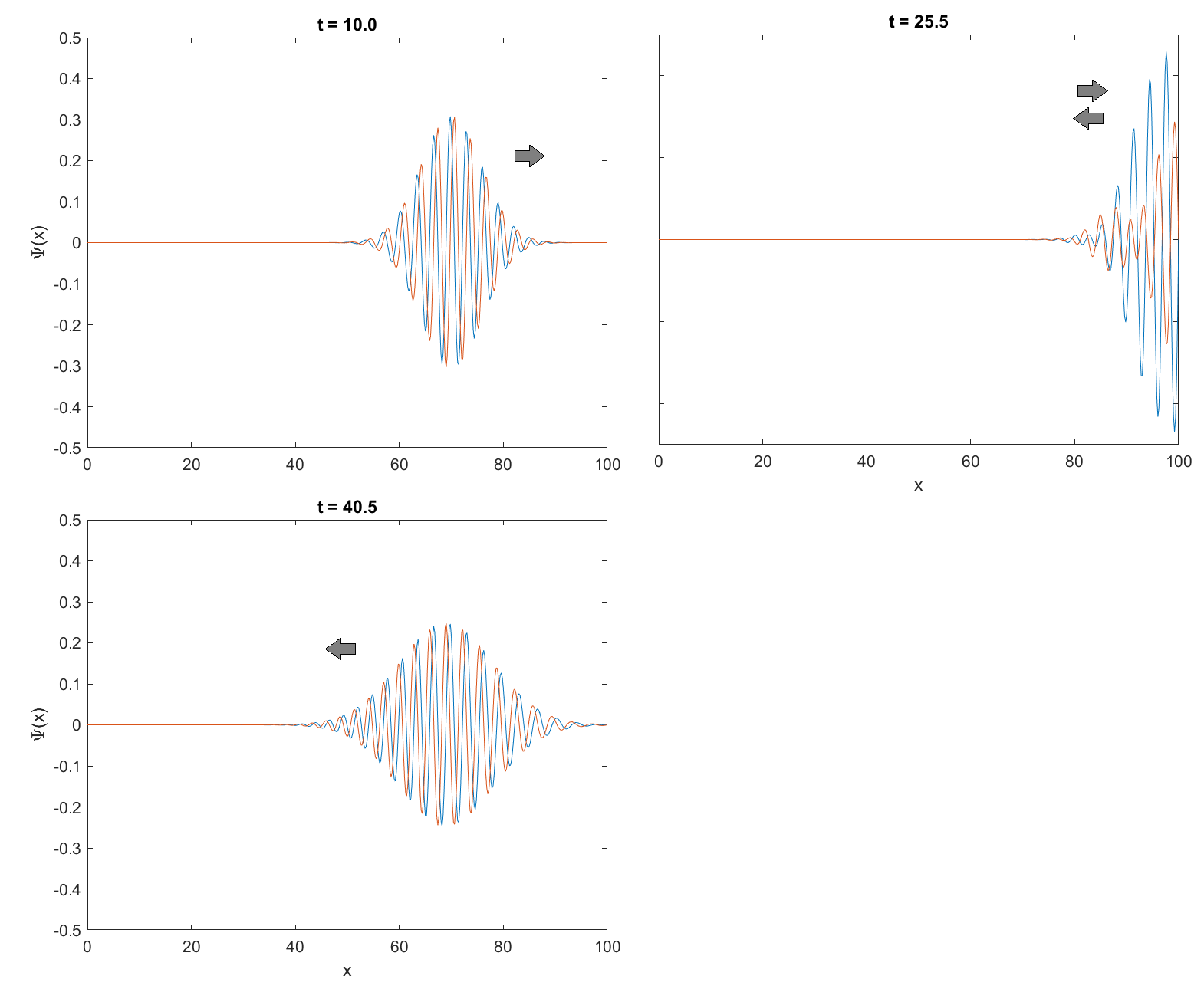
图 2:波包遇到势阱壁后发生反弹,过程中发生干涉
1. 计算
本文使用原子单位制,并假设粒子质量为 1。假设无限深势阱的区间为 $[0, L]$,能量的本征波函数(本征态)为(式 4 )
\begin{equation}
\psi _n(x) = \sqrt{\frac{2}{L}} \sin\left(k_n x\right) ~,
\end{equation}
\begin{equation}
k_n = \frac{n\pi }{L}~.
\end{equation}
\begin{equation}
E_n = \frac{k_n^2}{2}~.
\end{equation}
\begin{equation}
\psi (x,0) = \frac{1}{(2\pi \sigma _x ^2)^{1/4}} \mathrm{e} ^{-(x - x_0)^2/(2\sigma _x)^2} \mathrm{e} ^{ \mathrm{i} k_0x}~.
\end{equation}
第一步是把初始波函数投影到能量本征态上
\begin{equation}
C_n = \int_0^L \psi _n^*(x) \psi (x,0) \,\mathrm{d}{x}
= \int_0^L \sqrt{\frac{2}{L}} \sin\left(k_n x\right) \psi (x,0) \,\mathrm{d}{x} ~.
\end{equation}
\begin{equation}
\psi (x,t) = \sum _{i=0}^N C_i \mathrm{e} ^{- \mathrm{i} E_n t} \psi _n(x)~.
\end{equation}
若我们假设初始波包宽度足够小,使得波函数在势阱外的函数值可以忽略不计,则式 5 的定积分可以拓展到无穷区间,即傅里叶变换。我们已经知道初始高斯波包(指数)傅里叶变换的结果为式 2
\begin{equation}
g(k) = \frac{1}{(2\pi \sigma _p^2)^{1/4}} \mathrm{e} ^{-(k - k_0)^2/(2\sigma _k)^2} \mathrm{e} ^{- \mathrm{i} x_0(k - k_0)}~.
\end{equation}
\begin{equation}
\sqrt{\frac{2}{L}} \sin\left(k_n x\right) = \mathrm{i} \sqrt{\frac{\pi }{L}} \left(\frac{ \mathrm{e} ^{- \mathrm{i} k_n x}}{\sqrt{2\pi }} - \frac{ \mathrm{e} ^{ \mathrm{i} k_n x}}{\sqrt{2\pi }} \right) ~,
\end{equation}
\begin{equation}
C_n = \mathrm{i} \sqrt{\frac{\pi }{L}} [g(k_n) - g(-k_n)]~.
\end{equation}