简谐振子中的高斯波包模拟（Matlab）

贡献者： addis

预备知识　量子简谐振子（级数法），薛定谔方程 2（单粒子多维）

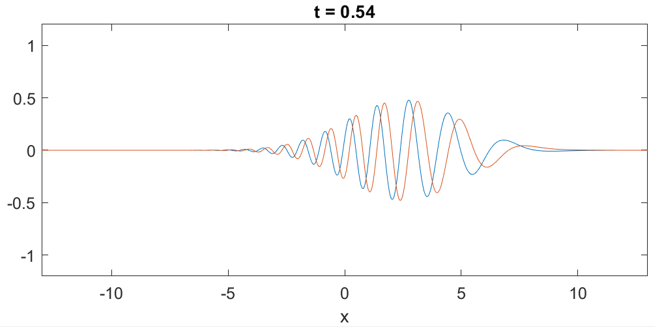
图 1：运行结果，动画见这里。

　　本文使用原子单位制。令无限深势阱的束缚态为 $\psi_n(x)$，含时波函数为 $\psi(x, t)$，已知 $\psi(x, 0)$，那么由式 9 得

\begin{equation} \psi(x, t) = \sum_{n=1}^\infty C_n\psi_n(x) \mathrm{e} ^{- \mathrm{i} E_n t}~. \end{equation}

其中

\begin{equation} C_n = \int_{-\infty}^{+\infty} \psi_n(x)\psi(x, 0) \,\mathrm{d}{x} \qquad (n=0,1,\dots)~. \end{equation}

　　注意经过一个周期后，波包模方的形状并不会改变，只是相位改变了。这和经典力学是相符的，根据经典的简谐振子模型，无论初始时刻质点的位置和速度是多少，一个周期后都会回到原位。

　　一般来说，波包扩散是因为初始时存在一定的速度分布。例如中心动量为零的波包经过较长时间 $t$ 后，位置分布就会趋近于初始动量分布乘以 $t$。

代码 1：SHOqm.m

% 高斯波包在简谐振子势阱中运动
function SHOqm
% === 参数 ===
m = 1; w = 1; % 质量，角频率
xmin = -13; xmax = 13; Nx = 500; % x 网格
tmin = 0; tmax = 2*pi/w; Nt = 200; % 时间网格
Nn = 70; % 束缚态的数量
x0 = 0; sig_x = 2; % 初始位置， 波包宽度
p0 = 5; % 初始动量
t0 = 0; % 高斯波包的初始时间
ax = [xmin, xmax, -1.2, 1.2]; % 坐标范围
% ===========
x = linspace(xmin, xmax, Nx);
psi_bound = zeros(Nn, Nx);

%% 计算并画前几个束缚态
figure;
for n = 0:Nn-1
    psi_bound(n+1,:) = psi_SHO(m, w, n, x);
    if n <= 4
        plot(x, psi_bound(n+1,:)); hold on; grid on;
    end
end
axis([-5, 5, -0.7, 0.8]);
xlabel x; title '\psi_n';
legend({'n=0','n=1','n=2','n=3','n=4'});

%% 计算高斯波包的初始展开系数
C = zeros(1, Nn);
psi_gs = @(x) 1/(2*pi*sig_x^2)^0.25/sqrt(1 + 1i*t0/(2*m*sig_x^2))...
      *exp(-(x-x0-p0*t0/m).^2/(2*sig_x)^2/(1 + 1i*t0/(2*m*sig_x^2)))...
      .*exp(1i*p0*(x-p0*t0/(2*m)));
plot(x, real(psi_gs(x)));

for n = 0:Nn-1
    psi_sho = @(x) psi_SHO(m, w, n, x);
    C(n+1) = integral(@(x) psi_sho(x).*psi_gs(x), xmin, xmax);
end
figure; plot(abs(C).^2);

%% 含时动画
figure; set(gcf, 'Unit', 'Normalized', 'Position', [0.1, 0.1, 0.4, 0.3]);
t = linspace(tmin, tmax, Nt);
for it = 1:Nt
    psi = zeros(1, Nx);
    for n = 0:Nn-1
        En = (0.5 + n)*w;
        psi = psi + C(n+1)*exp(-1i*En*t(it))*psi_bound(n+1,:);
    end
    clf;
    plot(x, real(psi)); hold on;
    plot(x, imag(psi)); axis(ax);
    xlabel x; title(['t = ' num2str(t(it), '%.2f')]);
    set(gca, 'FontSize', 12);
    saveas(gcf, [num2str(it), '.png']);
end
end

% 简谐振子束缚态波函数
function psi = psi_SHO(m, w, n, x)
alpha = sqrt(m*w); u = alpha * x;
psi = 1/sqrt(2^n*factorial(n)) *...
    (alpha^2/pi)^0.25 * hermiteH(n, u) .* exp(-u.^2/2);
end