贡献者: _Eden_
在固体物理学中,除了用近自由电子近似分析电子能带结构,还有一种方法,被称为紧束缚近似在一些场合的问题下是一个很好的近似,并且在计算和分析能带上能体现出一些优势。
在紧束缚近似模型中,一般假定电子受到了原子实很强的束缚作用,当它靠近一个原子实时,它的势场近似为库仑势。因此电子在原子实附近的行为和原子轨道波函数(类氢原子的束缚态)有一定的相关性。
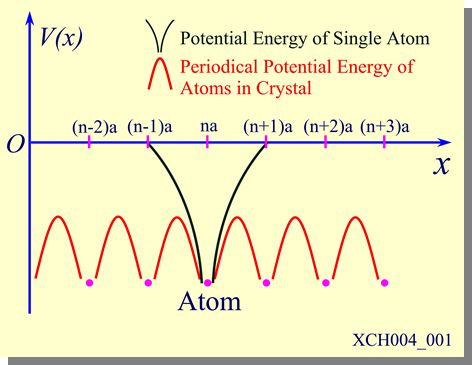
图 1:一维晶格的势场
由于势场是所有原子实产生的库仑势的叠加,所以在紧束缚近似模型中,假定在原子实附近的电子主要受该原子实的库仑势的影响,而将其他的原子实的库仑势对它的作用视为微扰。原子轨道波函数的能级是分立的,第 $n$ 个轨道对应 $n^2$ 个简并的态(不考虑自旋)。但如果引入其他原子实的势场微扰,这些能级就会发生劈裂,如下图所示。
图 2:紧束缚近似的能带示意图
1. 紧束缚近似的计算
假设 $V( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m)$ 为格点 $m$ 处的原子实产生的势场(一般可以近似视为库仑势场),设 $\phi_i( \boldsymbol{\mathbf{r}} )$ 为该势场下电子的束缚态波函数。那么根据核外电子的相关知识,我们知道 $\phi_i( \boldsymbol{\mathbf{r}} )$ 可以是 $s$ 轨道、$p$ 轨道波函数等等,并且可以由 $n,l,m$ 三个量子数来描述(不考虑自旋)。这些束缚态波函数满足
\begin{equation}
\left[-\frac{\hbar^2}{2m}\nabla^2+V( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m)\right]\phi_i( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m)=\epsilon_i\phi_i( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m)~.
\end{equation}
然而晶格的真正周期性势场 $U( \boldsymbol{\mathbf{r}} )$ 与 $V( \boldsymbol{\mathbf{r}} )$ 是有差距的,正如 图 1 所示。我们将 $U( \boldsymbol{\mathbf{r}} )-V( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m)$ 视为微扰哈密顿量。我们要求的波函数 $\psi( \boldsymbol{\mathbf{r}} )$ 满足
\begin{equation}
\left[-\frac{\hbar^2}{2m}\nabla^2+U( \boldsymbol{\mathbf{r}} ) \right] \psi( \boldsymbol{\mathbf{r}} )=E\psi( \boldsymbol{\mathbf{r}} )~.
\end{equation}
围绕不同的格点,在各自的势场 $V( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m),m=1,\cdots,N$ 下共有 $N$ 个束缚态波函数 $\phi_i( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m),m=1,\cdots,N$。我们利用原子轨道线性组合(LCAO)法,假设在周期性势场下,最终的电子波函数是这 $N$ 个束缚态波函数的线性叠加:
\begin{equation}
\psi( \boldsymbol{\mathbf{r}} )=\sum_{m} a_m \phi_i( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m)~.
\end{equation}
代入
式 2 后可以得到
\begin{equation}
\sum_{m} \left[\epsilon_i+(U( \boldsymbol{\mathbf{r}} )-V( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m) \right] a_m\phi_i( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m)=E\sum_{m} a_m\phi_i( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m)~.
\end{equation}
并且将不同格点处的束缚态波函数 $\phi_i( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m),m=1,\cdots,N$ 近似视为正交归一的。对
式 4 左乘 $\int \,\mathrm{d}{} ^3 \boldsymbol{\mathbf{r}} \phi_i^*( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _n)$,可以得到
\begin{equation}
\begin{aligned}
&\sum_m a_m \int \,\mathrm{d}{} ^3 \boldsymbol{\mathbf{r}} \phi_i^*( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _n)(U( \boldsymbol{\mathbf{r}} )-V( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m))\phi_i( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m)\\
&=a_n(E-\epsilon_i)~,
\end{aligned}
\end{equation}
注意到 $U( \boldsymbol{\mathbf{r}} )$ 是周期性势场。可以作换元 $ \boldsymbol{\mathbf{\xi}} = \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m$ 上式可以简写为
\begin{equation}
\begin{aligned}
&\sum_m a_m \int \,\mathrm{d}{} ^3 \boldsymbol{\mathbf{\xi}} \phi_i^*( \boldsymbol{\mathbf{\xi}} -( \boldsymbol{\mathbf{R}} _n- \boldsymbol{\mathbf{R}} _m))(U( \boldsymbol{\mathbf{\xi}} )-V( \boldsymbol{\mathbf{\xi}} ))\phi_i( \boldsymbol{\mathbf{\xi}} )
\\
&=-\sum_m a_m J( \boldsymbol{\mathbf{R}} _n- \boldsymbol{\mathbf{R}} _m)=a_n(E-\epsilon_i)~,
\end{aligned}
\end{equation}
其中设
\begin{equation}
\int \,\mathrm{d}{} ^3 \boldsymbol{\mathbf{\xi}} \phi_i^*( \boldsymbol{\mathbf{\xi}} - \boldsymbol{\mathbf{R}} )(U( \boldsymbol{\mathbf{\xi}} )-V( \boldsymbol{\mathbf{\xi}} ))\phi_i( \boldsymbol{\mathbf{\xi}} )=-J( \boldsymbol{\mathbf{R}} )~.
\end{equation}
$J$ 只有在 $\phi_i( \boldsymbol{\mathbf{R}} _n)$ 和 $\phi_i( \boldsymbol{\mathbf{R}} _m)$ 有交叠时才不为 $0$,所以被称为交叠积分或重叠积分。
以上方程的 $J( \boldsymbol{\mathbf{R}} _n- \boldsymbol{\mathbf{R}} _m)$ 只与格点 $n$ 与 $m$ 的相对位置有关,而我们考虑的是有周期性边界条件的晶格。由平移对称性,我们能够猜测系数 $a_m$ 具有平面波的形式:设 $a_m=C \exp\left(i \boldsymbol{\mathbf{k}} \cdot \boldsymbol{\mathbf{R}} _m\right) $,代入式 6 后可以得到
\begin{equation}
-C\sum_m J( \boldsymbol{\mathbf{R}} _n- \boldsymbol{\mathbf{R}} _m)\exp \left[-i \boldsymbol{\mathbf{k}} \cdot ( \boldsymbol{\mathbf{R}} _n- \boldsymbol{\mathbf{R}} _m) \right] =C(E-\epsilon_i)~.
\end{equation}
由于晶格具有周期性边界条件,可以对 $ \boldsymbol{\mathbf{R}} _n- \boldsymbol{\mathbf{R}} _m$ 进行换元。最后化简可以得到
\begin{equation}
E( \boldsymbol{\mathbf{k}} )=\epsilon_i-\sum_s J( \boldsymbol{\mathbf{R}} _s) \exp\left(-i \boldsymbol{\mathbf{k}} \cdot \boldsymbol{\mathbf{R}} _s\right) ~.
\end{equation}
波函数则可以写成 bloch 和的形式
\begin{equation}
\psi_{ \boldsymbol{\mathbf{k}} }( \boldsymbol{\mathbf{r}} )=\frac{1}{\sqrt{N}}\sum_m e^{i \boldsymbol{\mathbf{k}} \cdot \boldsymbol{\mathbf{R}} _m}\phi_i( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{R}} _m)=e^{i \boldsymbol{\mathbf{k}} \cdot \boldsymbol{\mathbf{r}} } \left(\frac{1}{\sqrt{N}}\sum_s e^{-i \boldsymbol{\mathbf{k}} \cdot \boldsymbol{\mathbf{R}} _s}\phi_i( \boldsymbol{\mathbf{R}} _s) \right) ~.
\end{equation}
由此可见,由紧束缚近似模型及原子轨道线性组合法得到的晶格中的电子波函数,是满足 Bloch 定理的(布洛赫理论)。
2. 能带计算
式 9 给出了紧束缚近似模型下晶格电子的色散关系,通过对它的计算,可以近似地画出能带。
例如,在一维单原子链晶格中,计算 $s$ 轨道波函数的 bloch 和,如果只考虑近邻格点的交叠函数 $J( \boldsymbol{\mathbf{R}} _s)$,那么有色散关系
\begin{equation}
E=\epsilon_s-J_0-J_1 e^{-i k a}-J_{-1}e^{ika}~.
\end{equation}
根据对称性,有 $J_1=J_{-1}$。并且我们可以通过
式 7 考察 $J_1$ 的正负性,一般而言 $U-V<0$,那么
式 7 的左侧积分值也是 $<0$ 的,所以 $J$ 通常 $>0$。
式 11 可以化简为
\begin{equation}
E=\epsilon_s-J_0-2J_1 \cos\left(ka\right) ~,
\end{equation}
$a$ 为晶格常数。由此画出的能带与
近自由电子模型求得的能带具有相似的特征,例如在能带的底部和顶部 $ \,\mathrm{d}{E} / \,\mathrm{d}{k} $ 为 $0$,在简约布里渊区边界 $\pm \pi/k$ 处能量最高。
在简单晶格中,则要考虑 $6$ 个方向上与近邻格点的交叠函数。在体心立方晶格中,一般要考虑 $8$ 个方向上的交叠函数;在面心立方晶格中则要考虑 $12$ 个方向上的交叠函数……在这种情况下,能带不是各向同性的,但有一定的对称性,可以看出这个对称性和晶格的对称性相符合。
对于复式晶格,即一个原胞中有两个或以上的原子,仍然可以采用上述的原子轨道线性组合法。以两个原子为例,考虑各自的 $s$ 轨道波函数。可以先对单个原胞中的两个原子利用原子轨道线性组合法计算,得到成键态和反键态(成键态的能量比反键态能量低),然后分别计算它们的 bloch 和……也可以对原胞中的每个原子单独求 bloch 和,然后再对求得的 bloch 和进行线性组合,最终只需求解一个较小的久期方程。