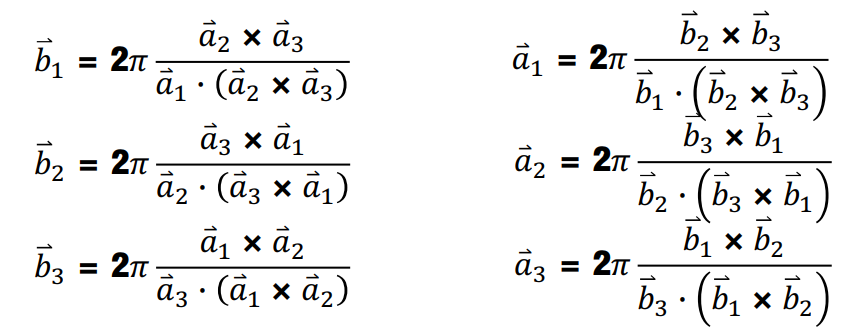贡献者: Zona
为了观测晶体结构,我们需要用特殊的方式对晶体进行探测。先了解一些基本知识:原子间距大约 $\sim 1$ nm,而人眼一般能看见的可见光波段在 $380 \sim 780 $ nm,这就使得利用可见光的干涉消长现象来推断晶体结构是不可能的事情。
为什么?假设你有一把尺子,每一格刻度最小为 $1$ mm。现在有一根头发丝,我们用尺子去测量它时,有办法直接精确测量出头发丝直径吗?显然很困难,我们的估算将会有很大误差。用波的干涉消长测量原子的间距,观察原子排布方式也是类似的原理。假设一束波长为 $10$ nm 的波入射,原子将紧密分布在波的每一个地方,相邻原子感受到的光场几乎相同,由此其散射光也几乎没有差异,我们无法得到干涉现象。
因此,需要将观测的入射波长缩小至 $\sim 1$ nm 乃至更小才能实现观测。怎么办?由物质波满足的德布罗意关系:
\begin{equation}
\lambda = \dfrac{p}{\hbar},~
\end{equation}
以及自由粒子满足的动能与动量关系:
\begin{equation}
E = \dfrac{p^2}{2 m}~.
\end{equation}
我们知道物质波的
波长反比于能量,波长越短,所需要的能量越高。室温下 $E \approx 26 $ meV 的电子对应的德布罗意波长 $\lambda \approx 7.6 $ nm;而波长 $1$ nm 的 X 射线能量在 $1240$ eV 左右,可以在钨等重元素中电子从外层向内层跃迁过程产生。为我们的观测提供了新的手段。
常用的实验观测手段有:
• X 射线衍射 (X-ray diffractio n)
• 低能电子衍射 (Low-energy electrondiffraction,LEED)
• 中子衍射 (Neutron diffraction)
• 角分辨光电子能谱 (Angle resolved photoe mission spectroscopy,ARPES)
1. 布拉格定律
有了实验观测现象,下一步是对衍射图样进行分析。1912 年,劳厄首先发现晶体 X 射线衍射现象,并给出了理论解释和一个比较复杂的衍射极大方向公式。第二年,布拉格父子给出了一个比劳厄方程更简单、更直接的公式。劳厄(Laue)和布拉格父子(Bragg)基于 X 射线衍射的晶体结构分析及其方程的建立,标志着近代固体物理学的开端。很快,1914 年,劳厄获得诺贝尔物理学奖;1915 年,布拉格父子获得诺贝尔物理学奖。
图 1:1927 年,在比利时布鲁塞尔举行的第五届索尔维国际会议
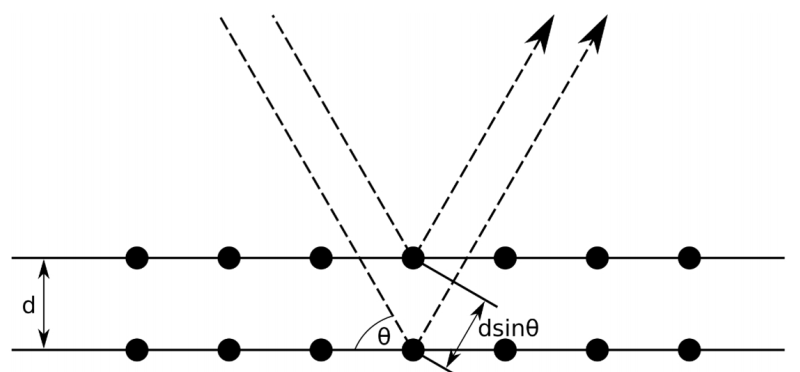
布拉格将晶体对 X 射线的衍射看成在晶面的反射。在不同晶面的反射满足布拉格定律时,反射波在该方向得到总体增强,形成衍射极大:
\begin{equation}
2d \cdot \sin\theta = n\lambda~,
\end{equation}
其中,$d$ 是相邻
晶面的距离,$n$ 是整数,$\theta$ 是入射波与晶面夹角。
图 2:布拉格衍射
推导上式需要读者有一定的光学基础。如果不会推也没关系,其物理结论即对于特定的入射角 $\theta$,可以观测到相干现象。这里有个问题:什么时候能把一个个原子的排列当成一面镜子来处理?答案是当入射波长远大于原子间距时。你可以想象,对于入射波来说,紧密排列的原子几乎是连续的。但 X 射线的波长接近原子间距,因此严格来说不能将原子当成镜面。
由此可见,布拉格对晶体 X 射线衍射的物理图像的描述是有问题的,但给出的结果是正确。下面我们看看劳厄方程的物理图像是什么样的。
2. 劳厄方程
劳厄将衍射看成不同原子对 X 射线的弹性散射。
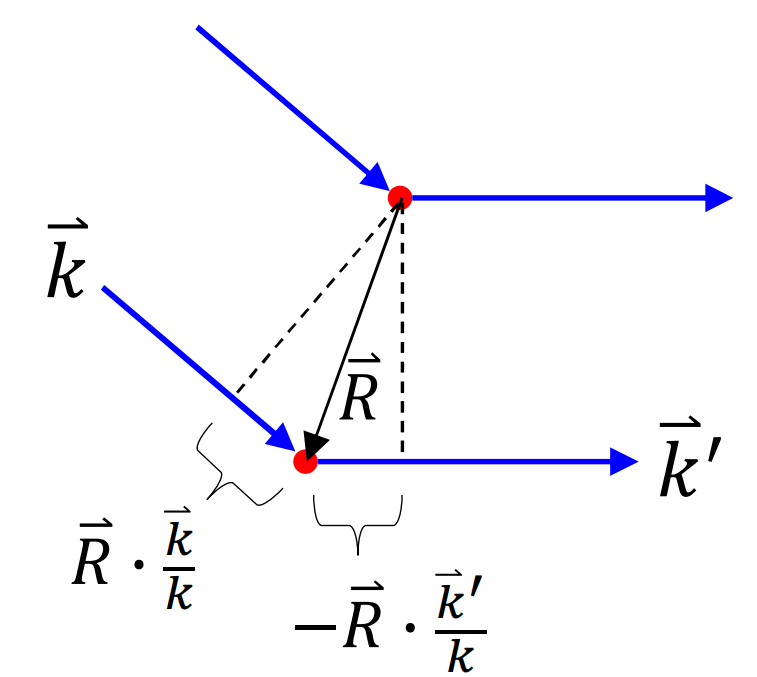
如图,红色圆点代表不同原胞内的原子,蓝线分别代表入射波 $ \boldsymbol{\mathbf{k}} $ 和出射波 $ \boldsymbol{\mathbf{k}} '$,格矢 $ \boldsymbol{\mathbf{R}} $ 是两个原胞之间的距离。发生弹性散射后得到的出射光与入射光频率相同,方向发生改变。
图 3:X 射线与原子发生弹性散射
要知道两束光之间干涉结果,需求出光程差:
\begin{equation}
\boldsymbol{\mathbf{R}} \boldsymbol\cdot \dfrac{ \boldsymbol{\mathbf{k}} }{k} - \boldsymbol{\mathbf{R}} \boldsymbol\cdot \dfrac{ \boldsymbol{\mathbf{k}} '}{k} ~,
\end{equation}
当光程差刚好是整数个波长时,射线形成衍射极大值
式 13 :
\begin{align}
\boldsymbol{\mathbf{R}} \boldsymbol\cdot \left(\dfrac{ \boldsymbol{\mathbf{k}} }{k} - \dfrac{ \boldsymbol{\mathbf{k}} '}{k} \right) &= n\lambda ~,\\
\end{align}
整理一下即:
\begin{equation}
\boldsymbol{\mathbf{R}} \boldsymbol\cdot ( \boldsymbol{\mathbf{k}} - \boldsymbol{\mathbf{k}} ') = 2n\pi~.
\end{equation}
这就是
劳厄方程。其中原子间距离是格矢 $ \boldsymbol{\mathbf{R}} = n_1 \boldsymbol{\mathbf{a}} _1 + n_1 \boldsymbol{\mathbf{a}} _2 + n_3 \boldsymbol{\mathbf{a}} _3$。
X 射线在任何两个不同原子上的散射方向满足劳厄方程时,在该方向上形成衍射极大值。劳厄方程是倒格空间许多概念的来源,例如:
3. 倒格矢
定义 1 倒格矢(reciprocal lattice vector)
对任意 $ \boldsymbol{\mathbf{R}} $ 都满足݊ $ \boldsymbol{\mathbf{R}} \boldsymbol\cdot \boldsymbol{\mathbf{G}} = 2 n \pi$($n$ 是整数)的矢量 $ \boldsymbol{\mathbf{G}} $ 称为倒格矢
。劳厄方程可改写为:
\begin{equation}
\boldsymbol{\mathbf{k}} - \boldsymbol{\mathbf{k}} ' = \boldsymbol{\mathbf{G}} ~.
\end{equation}
该式与
式 3 两者等价.
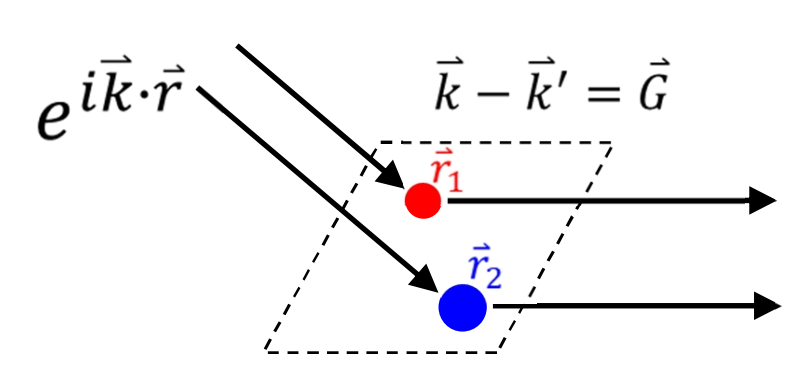
不过,劳厄方程并非衍射极大的充分必要条件。我们忽略了许多具体的影响因素,如不同原子对散射的效果不同,同一原胞内不同位置的原子散射效果也不同。因此需要对实际散射效果加上这些因素的影响,我们用一个未知函数 $f( \boldsymbol{\mathbf{G}} )$ 表示。
图 4:不同原子的散射效果不同
对于红色原子,相对于原点,衍射极大时的相位差为:
\begin{equation}
f_1( \boldsymbol{\mathbf{k}} - \boldsymbol{\mathbf{k}} ') e^{ \mathrm{i} ( \boldsymbol{\mathbf{k}} - \boldsymbol{\mathbf{k}} ') \boldsymbol\cdot \boldsymbol{\mathbf{r}} _1} =f_1( \boldsymbol{\mathbf{G}} ) e^{ \mathrm{i} \boldsymbol{\mathbf{G}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} _1}~,
\end{equation}
同理对于蓝色原子有:
\begin{equation}
f_2( \boldsymbol{\mathbf{G}} ) e^{ \mathrm{i} \boldsymbol{\mathbf{G}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} _2}~,
\end{equation}
总的散射效果为:
\begin{equation}
\boldsymbol{\mathbf{S}} ( \boldsymbol{\mathbf{G}} ) = f_1( \boldsymbol{\mathbf{G}} ) e^{ \mathrm{i} \boldsymbol{\mathbf{G}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} _1} + f_2( \boldsymbol{\mathbf{G}} ) e^{ \mathrm{i} \boldsymbol{\mathbf{G}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} _2}~.
\end{equation}
$S ( \boldsymbol{\mathbf{G}} )$ 为
结构因子,衍射峰的强度正比于 $|S( \boldsymbol{\mathbf{G}} )|^2$。这样,我们得到更准确的衍射峰表达式,具体 $f( \boldsymbol{\mathbf{G}} )$ 怎么写,依赖于晶体的构成。
4. 倒格空间
上面我们由衍射极大值给出了倒格矢的定义。满足劳厄方程的倒格矢有无数个(随着 $n$ 的取值而改变),我们如果描述这些处在动量空间的倒格矢呢?
实空间的格矢 $ \boldsymbol{\mathbf{R}} $ 有三个基矢 $ \boldsymbol{\mathbf{a}} _1, \boldsymbol{\mathbf{a}} _2, \boldsymbol{\mathbf{a}} _3$,不难联想,动量空间的倒格矢也应有三个基矢。我们称倒格矢所处的空间为倒格空间,倒格空间的基矢为倒格基矢:
定义 2 倒格基矢
倒格基矢 $ \boldsymbol{\mathbf{b}} _i$ 与 $ \boldsymbol{\mathbf{a}} _i$ 满足关系如下:
\begin{align}
\boldsymbol{\mathbf{a}} _i \boldsymbol\cdot \boldsymbol{\mathbf{b}} _j &= 2\pi \delta_{ij}~.
\end{align}
倒格矢可以表示为 $ \boldsymbol{\mathbf{G}} = m_1 \boldsymbol{\mathbf{b}} _1 + m_1 \boldsymbol{\mathbf{b}} _2 + m_3 \boldsymbol{\mathbf{b}} _3,~$ 其中 $ m_1,m_2,m_3 \in \mathrm{Z}$。
习题 1
利用倒格基矢的定义,证明劳厄方程 $ \boldsymbol{\mathbf{R}} \boldsymbol\cdot \boldsymbol{\mathbf{G}} = 2 n \pi$。
习题 2
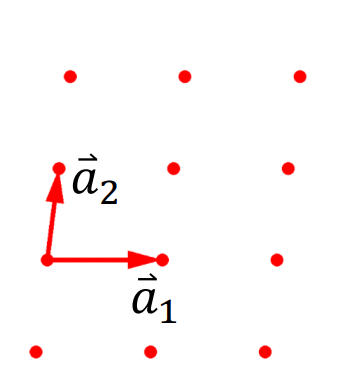
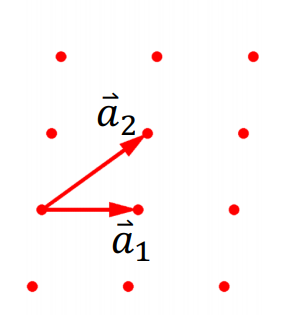
如图为二维情况下,实空间基矢的方向与大小,画出对应的倒格空间的倒格基矢。
图 5:二维实空间基矢
习题 3
会了吗?再做一题练练手呗。下面我们就要进入三维情况了。
图 6:还是二维实空间基矢
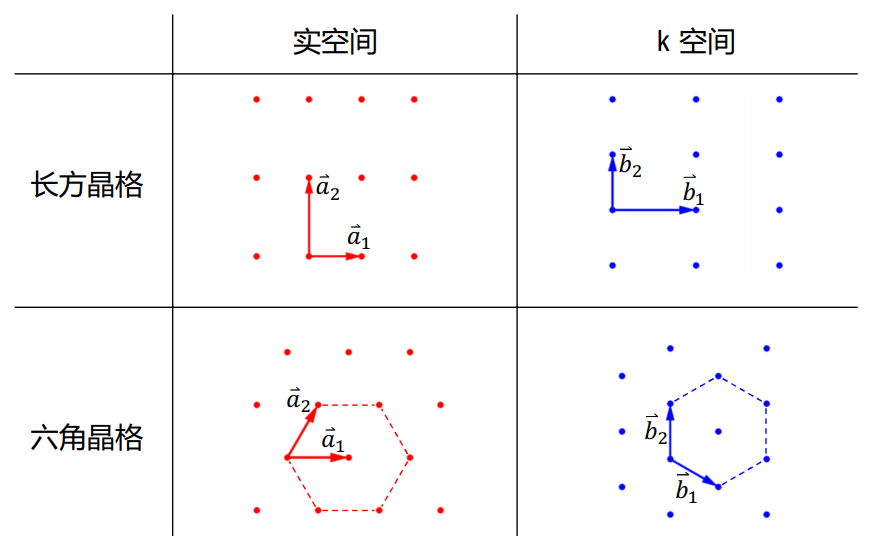
再看点图,加深印象:
图 7:二维倒格空间举例
三维情况下的倒格基矢与二维类似,$ \boldsymbol{\mathbf{b}} _3$ 垂直于 $ \boldsymbol{\mathbf{b}} _1 $ 和 $ \boldsymbol{\mathbf{b}} _2 $ 所在的平面。
习题 4
利用矢量运算关系,证明由左式可以推出右式。
图 8:三维晶格中 $ \boldsymbol{\mathbf{b}} $ 与 $ \boldsymbol{\mathbf{a}} $ 的关系
习题 5
设 $\Omega = | \boldsymbol{\mathbf{a}} _1 \boldsymbol\cdot ( \boldsymbol{\mathbf{a}} _2 \times \boldsymbol{\mathbf{a}} _3)|$ 是实空间的原胞体积,证明倒格基矢组成的平行六面体的体积为:
\begin{equation}
| \boldsymbol{\mathbf{b}} _1 \boldsymbol\cdot ( \boldsymbol{\mathbf{b}} _2 \times \boldsymbol{\mathbf{b}} _3)| = \dfrac{(2\pi)^3}{\Omega}~.
\end{equation}