贡献者: _Eden_; addis
经典统计理论用能量均分定理求得的金属中自由电子的热容与实际不符,这是经典统计理论的又一困难。1928 年索末菲(Sommerfeld)根据费米分布成功解决了这个问题。
金属中的自由电子互相碰撞的概率可忽略不计,自由电子与原子实碰撞的概率也可忽略不计。电子为费米子,可以将金属中的自由电子看成费米气体。
经典近似条件为 $e^{\alpha}\gg 1$,在这个条件下,费米分布可近似为玻尔兹曼分布。根据式 15 ,该条件等价于
\begin{equation}
\frac{V}{N} \left(\frac{2\pi mkT}{h^2} \right) ^{3/2}\gg 1~.
\end{equation}
电子的质量 $m$ 非常小,不满足该条件
1,在 $T=300K$ 时,$e^\alpha\approx 10^{-4}$。因此有显著的量子效应。我们必须用
费米分布来推导相关公式。
1. 低温极限下的电子气体
根据费米分布,温度为 $T$ 时能量 $\epsilon$ 上的一个量子态上的平均电子数为
\begin{equation}
f(\epsilon)=\frac{1}{e^{\frac{\epsilon-\mu}{kT}}+1}~.
\end{equation}
根据
式 2 ,在 $\epsilon\sim\epsilon+ \,\mathrm{d}{\epsilon} $ 间电子的量子态数为(考虑电子的自旋量子态,还要乘以 $2$)
\begin{equation}
D(\epsilon) \,\mathrm{d}{\epsilon} = \frac{4\pi V}{h^3}(2m)^{3/2}\epsilon^{1/2} \,\mathrm{d}{\epsilon} ~,
\end{equation}
所以总粒子数为
\begin{equation}
N=\frac{4\pi V}{h^3}(2m)^{3/2}\int_0^\infty \frac{\epsilon^{1/2} \,\mathrm{d}{\epsilon} }{e^{\frac{\epsilon-\mu}{kT}}+1}~.
\end{equation}
根据 $V,m,N$ 的值,可以由上式确定电子气体化学势 $\mu$。电子气体总能量为
\begin{equation}
E=\frac{4\pi V}{h^3}(2m)^{3/2}\int_0^\infty \frac{\epsilon^{3/2} \,\mathrm{d}{\epsilon} }{e^{\frac{\epsilon-\mu}{kT}}+1}~.
\end{equation}
上面出现的积分式被称为费米积分,很难求出解析解,但我们可以对 $T\rightarrow 0 \rm{K}$ 的情况求近似。
图 1:当温度 $T$ 较高时,$f(\epsilon )$ 关于 $\epsilon$ 的图像
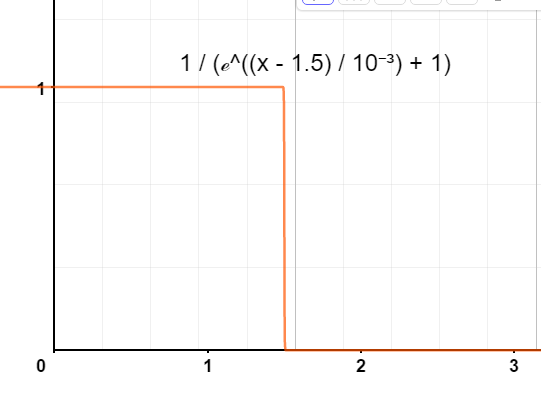
图 2:当温度 $T\rightarrow 0$ 时,$f(\epsilon )$ 关于 $\epsilon$ 的图像
如图 2 所示,当温度 $T\rightarrow 0$ 时,$f(\epsilon)$ 几乎成为阶梯函数。我们称温度 $0\rm{K}$ 时的电子气体的化学势 $\mu(0)$ 为费米能级(有时也记作 $\epsilon_F$)。当 $\epsilon<\mu(0)$ 时,$f(\epsilon)=1$,当 $\epsilon>\mu$ 时,$f(\epsilon)=0$。低于费米能级的量子态对应 $k$ 空间的一个费米球,称其球面为费米面。因此电子从最低能级开始一直填充到了费米面为止。因此
\begin{equation}
\begin{aligned}
N&=\frac{4\pi V}{h^3}(2m)^{3/2}\int_0^{\mu(0)}\epsilon^{1/2} \,\mathrm{d}{\epsilon}
\\
&=\frac{4\pi V}{h^3}(2m)^{3/2}\frac{2}{3}\mu(0)^{3/2}\\
\Rightarrow \mu(0)&=\frac{\hbar^2}{2m} \left(3\pi^2\frac{N}{V} \right) ^{2/3}~.
\end{aligned}
\end{equation}
由上式可得 $p_F=(3\pi^2n)^{1/3}\hbar$ 为 $0\rm{K}$ 时电子的最大动量,称为费米动量。设 $\mu(0)=kT_F$,定义 $T_F$ 为费米温度。对铜计算费米温度,可以得到 $T_F=8.2\times 10^4 \rm{K}$,这说明金属的 $\mu(0)$ 的数值通常很大。
$0K$ 时电子气体的动能为
\begin{equation}
\begin{aligned}
E&=\frac{4\pi V}{h^3}(2m)^{3/2}\int_0^{\mu(0)} \epsilon^{3/2} \,\mathrm{d}{\epsilon} \\
&=\frac{3}{5}N\mu(0)~,
\end{aligned}
\end{equation}
这说明 $0K$ 时电子的平均能量为 $\frac{3}{5}\mu(0)$。
可以看出电子的平均能量(或动能)与 $n^{2/3}$ 成正比,我们知道电子的平均势能与 $n^{1/3}$ 成正比,这说明只要电子气体稀疏到一定程度,电子的平均势能将大于电子的平均能量,其结果是电子将自动排布成势能低的晶格。Wigner 于 1934 年预言了这一种现象,然而这在普通金属中极难实现。1979 年人们在液氦表面吸附的二维电子气中证实了这种现象。
2. 自由电子气体的热容
早期 Drude 经典理论模型得出的结果是 $(3/2)k T$,这与实验结果不符。下面我们用费米-狄拉克分布来计算电子气体的热容,为此我们需要研究 $T\neq 0$ 的情况。
费米分布函数是复杂的,为此在作费米积分时往往作一些近似来简化计算。式 4 和式 5 可以统一成费米积分的形式:
\begin{equation}
I=\int_0^\infty H(\epsilon)f(\epsilon) \,\mathrm{d}{\epsilon} ~,
\end{equation}
作分布积分
\begin{equation}
I=Q(\epsilon)f(\epsilon)|_0^\infty + \int_0^\infty Q(\epsilon) \left(-\frac{\partial f}{\partial\epsilon} \right) \,\mathrm{d}{\epsilon} ~.
\end{equation}
其中
\begin{equation}
Q(\epsilon)=\int_0^\epsilon H(\epsilon') \,\mathrm{d}{\epsilon} '~.
\end{equation}
中的第一项为零,第二项中 $-\partial f/\partial \epsilon$ 是一个中心在 $\mu$ 处,宽度约为 $kT$ 的对称窄峰,因此 $Q(\epsilon)$ 函数在 $\mu$ 附近的取值才是对结果有影响的。我们对 $Q$ 作泰勒展开
\begin{equation}
Q(\epsilon)=Q(\mu)+(\epsilon-\mu)Q'(\mu)+\frac{1}{2}(\epsilon-\mu)^2 Q''(\mu)+\cdots~
\end{equation}
代入
式 9 ,并忽略高阶小项(二阶近似),可得
\begin{equation}
I\approx Q(\mu)+\frac{1}{2}Q''(\mu)\int_0^\infty (\epsilon-\mu)^2 \left(-\frac{\partial f}{\partial \epsilon} \right) \,\mathrm{d}{\epsilon} ~.
\end{equation}
第二项积分可以作二阶近似算出。最终解得(具体推导见
引理 1 )
\begin{equation}
I=Q(\mu)+\frac{\pi^2}{6}Q''(\mu)(k T)^2~,
\end{equation}
因此电子数的二阶近似公式为
\begin{equation}
\begin{aligned}
N&=\int_0^\infty D(\epsilon) f(\epsilon) \,\mathrm{d}{\epsilon} \approx
\int_0^\mu D(\epsilon) \,\mathrm{d}{\epsilon} + \frac{\pi^2}{6}D'(\mu)(kT)^2\\
&=\int_0^{\epsilon_F} D(\epsilon) \,\mathrm{d}{\epsilon} +(\mu-\epsilon_F) D(\epsilon_F) + \frac{\pi^2}{6}D'(\epsilon_F)(kT)^2~,
\end{aligned}
\end{equation}
其中第一项就是 $N$。因此我们得到了电子气体化学势 $\mu$ 在低温情况下的近似公式
\begin{equation}
\mu=\epsilon_F \left[1-\frac{\pi^2}{12} \left(\frac{kT}{\epsilon_F} \right) ^2 \right] ~.
\end{equation}
用类似的计算我们可以求出电子气体的内能
\begin{equation}
\begin{aligned}
u&=u_0+\frac{\pi^2}{6}g(\epsilon_F)(kT)^2\\
&=u_0 \left[1+\frac{5}{12}\pi^2 \left(\frac{T}{T_F} \right) ^2 \right] ~,
\end{aligned}
\end{equation}
因此电子气体(在低温情况下)的比热为
\begin{equation}
c_V=\left(\frac{\partial u}{\partial T}\right)_n=\frac{\pi^2}{3}k^2 g(\epsilon_F) T =\frac{\pi^2}{2}nk\frac{T}{T_F}= \gamma T~,
\end{equation}
结合上固体热容的德拜理论(它计算的是离子实系统的比热),金属的总比热可以写成
\begin{equation}
c_V=\gamma T+\beta T^3~.
\end{equation}
3. 附录
引理 1 费米型积分练习
证明:在低温的情况下,下式成立(其中 $f(\epsilon)$ 由 式 2 给出):
\begin{equation}
\int_0^\infty (\epsilon-\mu)^2 \left(-\frac{\partial f}{\partial \epsilon} \right) \,\mathrm{d}{\epsilon}
\approx\frac{\pi^2}{3}(kT)^2~.
\end{equation}
证明:由于 $-\partial f/\partial \epsilon$ 的图像是一个宽约 $k T$ 的尖峰,所以可以作如下近似
\begin{equation}
\begin{aligned}
I&=\int_0^\infty 2x^2 \left(-\frac{\partial f(\mu+x)}{\partial x} \right) \,\mathrm{d}{x} \\
&=\int_0^\infty 4x f(\mu+x) \,\mathrm{d}{x} \\
&=\int_0^\infty \frac{4x \,\mathrm{d}{x} }{e^{x/kT}+1}~.
\end{aligned}
\end{equation}
对 $1/(e^{x/kT}+1)$ 作级数展开
\begin{equation}
\begin{aligned}
I&=\int_0^\infty \frac{4x \,\mathrm{d}{x} }{e^{x/kT}} \left(1-\frac{1}{e^{x/kT}}+\frac{1}{e^{2x/kT}}-\cdots \right) \\
&=4(kT)^2 \left(1-\frac{1}{2^2}+\frac{1}{3^2}-\cdots \right) \\
&=4(kT)^2 \left(\zeta(2)-\frac{1}{2}\zeta(2) \right) =\frac{\pi^2}{3}(kT)^2~,
\end{aligned}
\end{equation}
上面的推导中利用了
黎曼 $\zeta$ 函数在 $z=2$ 处的取值。
1. ^ 以铜为例,铜的密度是 $8.9\times 10^3 \rm{kg\cdot m^{-3}}$,相对原子质量为 $63.5$,如果一个铜原子贡献一个自由电子,则 $N/V=n=8.5\times 10^{28} m^{-3}$。电子的质量为 $9.1\cdot 10^{-31} \rm{kg}$,于是 $e^\alpha=\frac{V}{N} \left(\frac{2\pi m kT}{h^2} \right) ^{3/2}=2.8\cdot 10^{-8}T^{3/2}$