贡献者: Zona; addis; _Eden_
在固体物理中,我们研究原子按一定规则排布而成的理想晶格,研究电子在一个具有晶格周期性的等效势场 $V( \boldsymbol{\mathbf{r}} )$ 中的运动。根据定态薛定谔方程,我们有
\begin{equation}
H\psi= \left[-\frac{\hbar^2}{2m}\nabla^2+V( \boldsymbol{\mathbf{r}} ) \right] \psi = E\psi~,
\end{equation}
势场 $V( \boldsymbol{\mathbf{r}} )$ 满足周期性
\begin{equation}
V( \boldsymbol{\mathbf{r}} )=V( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} _n)~,
\end{equation}
其中 $ \boldsymbol{\mathbf{R}} _n$ 为任意晶格矢量。
为了研究周期性势场下定态薛定谔方程的解,我们可以从最简单的一维薛定谔方程出发。
1. Bloch theory
1布洛赫(Bloch)理论也叫 Floquet 理论,是由对称性得到的严格结论。它的内容可以表述如下:
定理 1 Bloch theory I
周期势场 $V( \boldsymbol{\mathbf{r}} ) = V( \boldsymbol{\mathbf{k}} + \boldsymbol{\mathbf{R}} )$ 下的本征态波函数满足
\begin{equation}
\psi( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} ) = \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{R}} }\psi( \boldsymbol{\mathbf{r}} )~,
\end{equation}
其中 $ \boldsymbol{\mathbf{k}} $ 的量纲是 $[L^{-1}]$,$ \boldsymbol{\mathbf{R}} $ 是晶格矢量,简称为
格矢。后面我们将会看到,$ \boldsymbol{\mathbf{k}} $ 具有动量的物理意义,是电子的动量的一部分,称为
波矢。
也就是说,将空间坐标 $ \boldsymbol{\mathbf{r}} $ 平移格矢 $ \boldsymbol{\mathbf{R}} $,平移前后的波函数只相差一个跟 $ \boldsymbol{\mathbf{R}} $ 有关的相位因子,不改变波函数本身的物理性质。
$\psi ( \boldsymbol{\mathbf{r}} )$ 称为布洛赫函数(Bloch function),晶体中用布洛赫函数来描述的电子称为布洛赫电子,与真空中的自由电子区分。
布洛赫定理的另一种等价描述为:
定理 2 Bloch theory II
周期势场中的本征态函数 $\psi( \boldsymbol{\mathbf{r}} )$ 可写成一个平面波和周期性函数的乘积:
\begin{equation}
\psi( \boldsymbol{\mathbf{r}} ) = \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} } u( \boldsymbol{\mathbf{r}} )~.
\end{equation}
$u( \boldsymbol{\mathbf{r}} )$ 是布洛赫函数的
周期部分,周期为 $ \boldsymbol{\mathbf{R}} $,$ \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} }$ 是平面波部分。
从 Bloch 定理的等价描述中,我们可以初步看到,布洛赫函数是真空中自由电子的平面波受到周期性势场的调制的结果。
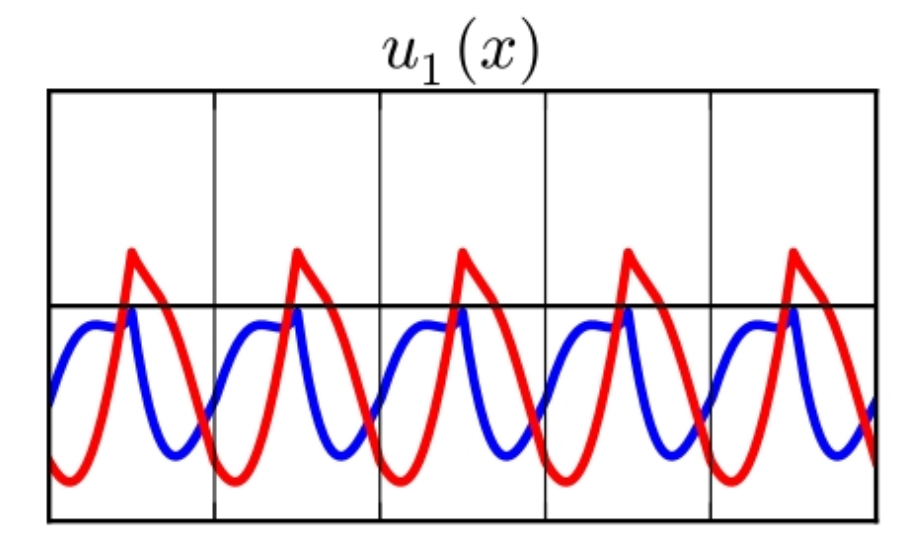
图 1:周期函数 $u_1$,蓝线为实部,红线为虚部。
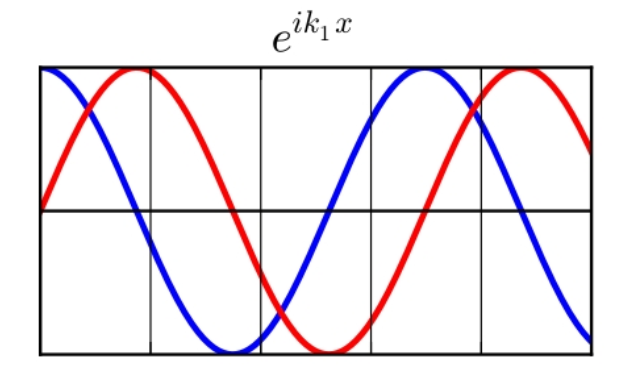
图 2:一维平面波 $ \mathrm{e} ^{ \mathrm{i} k_1 x}$
图 3:一维布洛赫函数 $\psi(x)$
习题 1
请根据定理证明两种描述的等价性。答案在下面。
由式 3 到式 4 ,等式两边同乘 $ \mathrm{e} ^{- \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot ( \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{r}} )}$:
\begin{equation}
\mathrm{e} ^{- \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot ( \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{r}} )}\psi( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} ) = \mathrm{e} ^{- \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} }\psi( \boldsymbol{\mathbf{r}} )~,
\end{equation}
观察左右两式,可以看到明显的周期函数:
\begin{equation}
u( \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{r}} ) = u( \boldsymbol{\mathbf{r}} ),~\quad u( \boldsymbol{\mathbf{r}} ) = \mathrm{e} ^{- \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} }\psi( \boldsymbol{\mathbf{r}} )~.
\end{equation}
整理一下,也即
\begin{equation}
\psi( \boldsymbol{\mathbf{r}} ) = \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} } u( \boldsymbol{\mathbf{r}} )~.
\end{equation}
证毕。由
式 4 到
式 3 :
\begin{align}
\psi( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} ) &= \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot ( \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{r}} )} u( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} )\\
&= \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{R}} } \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} }u( \boldsymbol{\mathbf{r}} )\\ &= \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{R}} } \psi( \boldsymbol{\mathbf{r}} )~.
\end{align}
证毕。
布洛赫定理的量子力学证明
上面我们从数学角度出发,仅利用了函数的周期性性质。下面用量子力学的语言证明 Bloch 定理,即周期性空间平移的效果仅是给波函数添加 phase shift, 不改变物理实质。
定义平移算符 $\hat{T}_{ \boldsymbol{\mathbf{R}} }$,将 $\hat{T}_{ \boldsymbol{\mathbf{R}} }$ 作用到任何函数 $f( \boldsymbol{\mathbf{r}} )$ 上的作用是:
\begin{equation}
\hat{T}_{ \boldsymbol{\mathbf{R}} } f( \boldsymbol{\mathbf{r}} ) = f( \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{r}} )~,
\end{equation}
也即将函数的坐标平移矢量 $ \boldsymbol{\mathbf{R}} $,这里 $ \boldsymbol{\mathbf{R}} = n_1 \boldsymbol{\mathbf{a}} _1 + n_2 \boldsymbol{\mathbf{a}} _2 + n_3 \boldsymbol{\mathbf{a}} _3 $ 是任意格矢。我们可以想到,如果对函数 $f( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} )$ 再平移一次空间坐标 $ \boldsymbol{\mathbf{R}} '$,则应得到 $f( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{R}} ')$,其效果等价于对 $f( \boldsymbol{\mathbf{r}} )$ 平移坐标 $ \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{R}} '$,也即:
\begin{equation}
\hat{T}_{ \boldsymbol{\mathbf{R}} '}\hat{T}_{ \boldsymbol{\mathbf{R}} } f( \boldsymbol{\mathbf{r}} ) = \hat{T}_{ \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{R}} '}f( \boldsymbol{\mathbf{r}} )~.
\end{equation}
从物理直觉上,晶体的周期性势场使得周期性平移不改变电子所处的晶格系统的哈密顿量,也即能量守恒。下面将从数学角度证明哈密顿量与平移算符的对易性。
\begin{equation}
\begin{aligned}
\hat{T}_{ \boldsymbol{\mathbf{R}} } \hat{H} f( \boldsymbol{\mathbf{r}} ) &= \hat{T}_{ \boldsymbol{\mathbf{R}} } \left[ \left(-\frac{\hbar^2}{2m}\nabla^2+V( \boldsymbol{\mathbf{r}} ) \right) f( \boldsymbol{\mathbf{r}} ) \right] \\
&= \left[-\frac{\hbar^2}{2m}\nabla^2+V( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} ) \right] f( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} )\\
&= \left[-\frac{\hbar^2}{2m}\nabla^2+V( \boldsymbol{\mathbf{r}} ) \right] f( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} )\\
& = \hat{H} \hat{T}_{ \boldsymbol{\mathbf{R}} } f( \boldsymbol{\mathbf{r}} )~.
\end{aligned}
\end{equation}
写成对易算符形式,也即
\begin{equation}
[\hat{T},\hat{H}] = 0~.
\end{equation}
因此,平移算符 $\hat{T}$ 存在和能量 $\hat{H}$ 相同的本征态。
为什么我们要关注它的对易性呢?因为
式 3 实际上是波函数的本征方程,我们要证明平移算符的本征值为与 $ \boldsymbol{\mathbf{R}} $ 有关的相因子,就要先探究它的本征值长什么样。
设哈密顿量的本征态为 $\psi$,由算符对易性可知,$\psi$ 也是算符 $\hat{T}$ 的本征态:
\begin{equation}
\hat{T}_{ \boldsymbol{\mathbf{R}} } \psi ( \boldsymbol{\mathbf{r}} ) = \lambda_{ \boldsymbol{\mathbf{R}} }\psi =\psi( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} )~,
\end{equation}
由波函数的归一化性质可知,$|\lambda_{ \boldsymbol{\mathbf{R}} } |^2 = 1,~ \lambda_{ \boldsymbol{\mathbf{R}} } = \mathrm{e} ^{ \mathrm{i} \beta}$。利用平移算符的性质
\begin{equation}
\hat{T}_{ \boldsymbol{\mathbf{R}} '} \hat{T}_{ \boldsymbol{\mathbf{R}} }\psi ( \boldsymbol{\mathbf{r}} ) = \lambda_{ \boldsymbol{\mathbf{R}} '}\lambda_{ \boldsymbol{\mathbf{R}} }\psi ( \boldsymbol{\mathbf{r}} ) = \lambda_{ \boldsymbol{\mathbf{R}} ' + \boldsymbol{\mathbf{R}} } \psi ( \boldsymbol{\mathbf{r}} )~,
\end{equation}
\begin{equation}
\lambda_{ \boldsymbol{\mathbf{R}} '}\lambda_{ \boldsymbol{\mathbf{R}} } = \lambda_{ \boldsymbol{\mathbf{R}} ' + \boldsymbol{\mathbf{R}} }~,
\end{equation}
\begin{equation}
\mathrm{e} ^{ \mathrm{i} (\beta_{ \boldsymbol{\mathbf{R}} '}+ \beta_{ \boldsymbol{\mathbf{R}} })} = \mathrm{e} ^{ \mathrm{i} \beta_{ \boldsymbol{\mathbf{R}} + \boldsymbol{\mathbf{R}} '}}~,
\end{equation}
可以看到,$\beta$ 是 $ \boldsymbol{\mathbf{R}} $ 的线性函数,不妨设
\begin{equation}
\lambda_{ \boldsymbol{\mathbf{R}} } = \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{R}} }~,
\end{equation}
这就是我们要求的平移算符的本征值。其中 $ \boldsymbol{\mathbf{k}} $ 是待定的常量。注意,由于不同的平移算符本征值对于不同的本征态,因此我们可以用 $ \boldsymbol{\mathbf{k}} $ 来区分这些本征态,记为 $\psi_{ \boldsymbol{\mathbf{k}} } ( \boldsymbol{\mathbf{r}} )$。最后,将本征值代入
式 15 ,我们就证明了布洛赫定理
式 3 。
也许初入量子力学的读者会对这些算符操作产生困惑,因为从表面上看起来,它们和物理实质并不挂钩,依然仅是一通数学操作。但我们要明白,算符操作实际上是将物理意义映射在线性代数空间下的数学操作,看起来抽象的数学,本质上依然是在为物理服务。每一步操作下,都有它们对应的物理含义。
物理意义
不同原胞内的电子具有相同的密度分布:
\begin{equation}
|\psi( \boldsymbol{\mathbf{r}} )|^2 = |u( \boldsymbol{\mathbf{r}} )|^2 = |\psi( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} )|^2~,
\end{equation}
而波函数仅相差一个相因子,因此,从一个原胞的电子波函数出发,就可以得到电子在整个晶体中的状态。这就是周期性势场带来的效果。
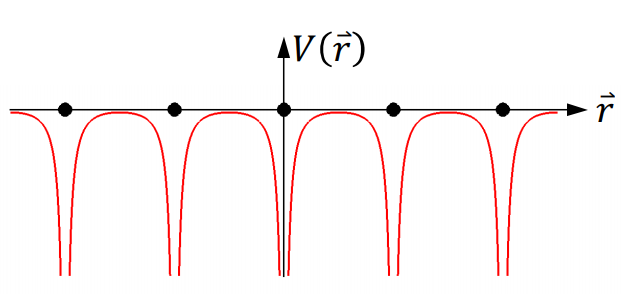
图 4:晶体中的周期性势场
2. 波矢 $ \boldsymbol{\mathbf{k}} $ 的物理意义
从上述量子力学的推导过程中我们可以看到,本质上 $ \boldsymbol{\mathbf{k}} $ 来源于平移算符的本征值:
\begin{equation}
\hat{T}_{ \boldsymbol{\mathbf{R}} } \psi ( \boldsymbol{\mathbf{r}} ) = \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{R}} }\psi ( \boldsymbol{\mathbf{r}} )~,
\end{equation}
因此,真正有意义的、用于描述电子状态在空间平移下性质的是相位因子 $ \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{R}} }$,而非 $ \boldsymbol{\mathbf{k}} $ 本身。
那 $\hbar \boldsymbol{\mathbf{k}} $ 又代表什么呢?乍一看像是电子的动量。且慢,让我们仔细算算动量算符 $\hat{p}$ 的本征值:
\begin{equation}
\begin{aligned}
\hat{p} \psi_{ \boldsymbol{\mathbf{k}} } ( \boldsymbol{\mathbf{r}} ) &= - \mathrm{i} \hbar \dfrac{\partial}{\partial \boldsymbol{\mathbf{r}} } \left( \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} } u( \boldsymbol{\mathbf{r}} ) \right) \\
& = \hbar \boldsymbol{\mathbf{k}} \psi_{ \boldsymbol{\mathbf{k}} } ( \boldsymbol{\mathbf{r}} ) - \mathrm{i} \hbar \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} } \dfrac{\partial u( \boldsymbol{\mathbf{r}} )}{\partial \boldsymbol{\mathbf{r}} }\\
&\neq \hbar \boldsymbol{\mathbf{k}} \psi_{ \boldsymbol{\mathbf{k}} } ( \boldsymbol{\mathbf{r}} )\\~.
\end{aligned}
\end{equation}
所以 $ \boldsymbol{\mathbf{k}} $ 仅是电子动量的一部分。
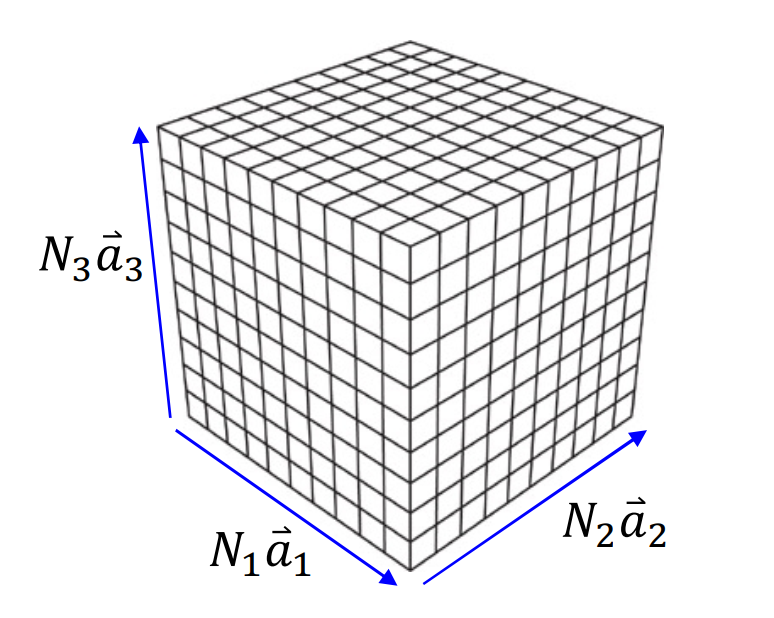
$ \boldsymbol{\mathbf{k}} $ 可以取任意值吗?从直觉上这是不可能的,一方面无限大动能的电子不存在,另一方面如果电子动能很大,它早就跑出晶体了。所以我们需要考虑 $ \boldsymbol{\mathbf{k}} $ 满足的限制条件:周期平移不变性。实际晶体不是无穷大的,周期性平移电子总会跑出晶体之外,这该怎么办?物理学家常用的处理方法是将其 “绕回去”,引入周期性边界条件:设晶格在三个方向上的原胞数量分别为 $N_1,N_2,N_3$,则平移 $N_1$ 个原胞后得到的波函数与初态相同,又回去了:
\begin{equation}
\hat T _{N_1 \boldsymbol{\mathbf{a}} _1}\psi_{ \boldsymbol{\mathbf{k}} }( \boldsymbol{\mathbf{r}} )=\psi_{ \boldsymbol{\mathbf{k}} }( \boldsymbol{\mathbf{r}} +N_1 \boldsymbol{\mathbf{a}} _1) = \psi_{ \boldsymbol{\mathbf{k}} }( \boldsymbol{\mathbf{r}} )~,
\end{equation}
其中 $ \boldsymbol{\mathbf{a}} _1$ 是 $x$ 方向的原胞基矢,$N_1$ 是 $x$ 方向总共的原胞数目。则有:
\begin{equation}
e^{ \mathrm{i} N_1 \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{a}} _1} = 1,~ k_1 =\frac{2\pi m_1}{N_1}~.
\end{equation}
同理,沿 $y$,$z$ 方向也满足周期性条件,综上给出的 $ \boldsymbol{\mathbf{k}} $ 是
离散化的:
\begin{equation}
\boldsymbol{\mathbf{k}} = \dfrac{m_1}{N_1 a_1} \boldsymbol{\mathbf{b}} _1 + \dfrac{m_2}{N_2 a_2} \boldsymbol{\mathbf{b}} _2 + \dfrac{m_3}{N_3 a_3} \boldsymbol{\mathbf{b}} _3,~ m_1,m_2,m_3 \in \mathbb{Z}~.
\end{equation}
其中 $ \boldsymbol{\mathbf{b}} _1, \boldsymbol{\mathbf{b}} _2, \boldsymbol{\mathbf{b}} _3$ 是倒格基矢。利用倒格基矢与基矢的关系 $ \boldsymbol{\mathbf{a}} _i \boldsymbol{\mathbf{b}} _j = 2\pi \delta_{ij}$,则可将 $ \boldsymbol{\mathbf{k}} $ 的表达式化简如上式。
图 5:由原胞组成的晶体
未完成:增加倒格基矢、倒格空间等相关的文章
3. 一维布洛赫函数
在一维情况下,波函数可以记为
\begin{equation}
\psi(x) = e^{ \mathrm{i} K x} u(x)~,
\end{equation}
其中 $u(x)$ 是一个周期为 $a$ 的函数。也就是波函数是一个振幅受周期性调制的平面波。
如果我们施加循环边界条件($N$ 是晶体一个方向的原子数,阿伏伽德罗常数数量级)
\begin{equation}
\psi(x+Na) = \psi(x)~,
\end{equation}
得
\begin{equation}
K = \frac{2\pi}{a} \frac{n}{N} \qquad (n \in \mathbb Z)~,
\end{equation}
一个例子见一维 delta 势能晶格。
4. 三维布洛赫函数
[1] [2] 布洛赫(Bloch)波函数定义为
\begin{equation}
\phi( \boldsymbol{\mathbf{r}} ) = \mathrm{e} ^{ \mathrm{i} \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{r}} } u( \boldsymbol{\mathbf{r}} )~,
\end{equation}
其中 $u( \boldsymbol{\mathbf{r}} )$ 具有与晶格同样的周期性。
\begin{equation}
u( \boldsymbol{\mathbf{r}} )=u( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{R}} _n)~,
\end{equation}
$ \boldsymbol{\mathbf{R}} _n$ 为晶格矢量。即在任何平移 $ \boldsymbol{\mathbf{R}} _n$ 的操作下势场 $V( \boldsymbol{\mathbf{r}} )$ 都是不变的。我们引入描述晶格平移对称性的算符 $T_1,T_2,T_3$,它们的定义是
\begin{equation}
T_\alpha u( \boldsymbol{\mathbf{r}} )= u( \boldsymbol{\mathbf{r}} + \boldsymbol{\mathbf{a}} _\alpha),\alpha=1,2,3~,
\end{equation}
其中 $ \boldsymbol{\mathbf{a}} _\alpha,\alpha=1,2,3$ 是晶格的三个基矢。它们是相互对易的,而且容易证明它们和哈密顿算符 $H$ 也相互对易。下面我们要做的就是找出 $H,T_1,T_2,T_3$ 的共同本征态,用以描述晶格中的电子。设
\begin{equation}
\begin{aligned}
&H\psi=E\psi,\\
&T_\alpha \psi = \lambda_\alpha \psi, \alpha=1,2,3~.
\end{aligned}
\end{equation}
设晶格在三个方向上的原胞数量分别为 $N_1,N_2,N_3$,那么可以引入晶格的周期性边界条件:
\begin{equation}
\psi( \boldsymbol{\mathbf{r}} )=\psi( \boldsymbol{\mathbf{r}} +N_\alpha \boldsymbol{\mathbf{a}} _\alpha),\alpha=1,2,3~
\end{equation}
可以得出 $\lambda_\alpha$ 具有下列形式
\begin{equation}
\lambda_\alpha=e^{ \dfrac{2\pi i l_\alpha}{N_\alpha}}~,
\end{equation}
其中 $l_\alpha$ 为整数。
如果引入倒格子矢量 $ \boldsymbol{\mathbf{b}} _1, \boldsymbol{\mathbf{b}} _2, \boldsymbol{\mathbf{b}} _3$,满足 $ \boldsymbol{\mathbf{a}} _i \boldsymbol\cdot \boldsymbol{\mathbf{b}} _j = 2\pi \delta_{ij}$,那么
\begin{equation}
\begin{aligned}
&\lambda_\alpha = e^{i \boldsymbol{\mathbf{k}} \boldsymbol\cdot \boldsymbol{\mathbf{a}} _\alpha}\\
& \boldsymbol{\mathbf{k}} =\sum_\alpha\frac{l_\alpha}{N_\alpha} \boldsymbol{\mathbf{b}} _\alpha~.
\end{aligned}
\end{equation}
我们可以将
式 4 三维晶格的布洛赫定理写成以下形式
\begin{equation}
\begin{aligned}
\psi \left( \boldsymbol{\mathbf{r}} +\sum_\alpha m_\alpha \boldsymbol{\mathbf{a}} _\alpha \right) &= T_1^{m_1} T_2^{m_2} T_3^{m_3} \psi( \boldsymbol{\mathbf{r}} )\\
&=e^{i \boldsymbol{\mathbf{k}} \boldsymbol\cdot \left(\sum_\alpha m_\alpha \boldsymbol{\mathbf{a}} _\alpha \right) }\psi( \boldsymbol{\mathbf{r}} )~.
\end{aligned}
\end{equation}
其中 $ \boldsymbol{\mathbf{k}} $ 称为简约波矢,它对应于平移算符操作本征值的量子数 $l_1,l_2,l_3$。注意到当 $l_\alpha$ 增加 $N_\alpha$ 时 $\lambda_\alpha$ 没有发生变化,所以我们将 $l_\alpha$ 限制在 $0 \boldsymbol\cdot s N_\alpha-1$ 因此得到简约波矢与量子数的一一对应。这相当于把 $ \boldsymbol{\mathbf{k}} $ 限制在 $ \boldsymbol{\mathbf{k}} $ 空间中由 $ \boldsymbol{\mathbf{b}} _1, \boldsymbol{\mathbf{b}} _2, \boldsymbol{\mathbf{b}} _3$ 构成的原胞中,$ \boldsymbol{\mathbf{k}} $ 的允许值个数为 $N_1N_2N_3$,也就是晶体的原胞总数。另一种更方便的方式,是将 $ \boldsymbol{\mathbf{k}} $ 限制在 $ \boldsymbol{\mathbf{k}} $ 空间的维格纳塞茨原胞中,这个区域被称为第一布里渊区。
1. ^ 参考 [3]
[1] ^ 黄昆. 固体物理学 高等教育出版社
[2] ^ Bransden, Physics of Atoms and Molecules, 2ed
[3] ^ David Griffiths, Introduction to Quantum Mechanics, 4ed