大气密度和压强

贡献者： addis; _Eden_

预备知识　一阶线性微分方程，理想气体分压定律，积分方程

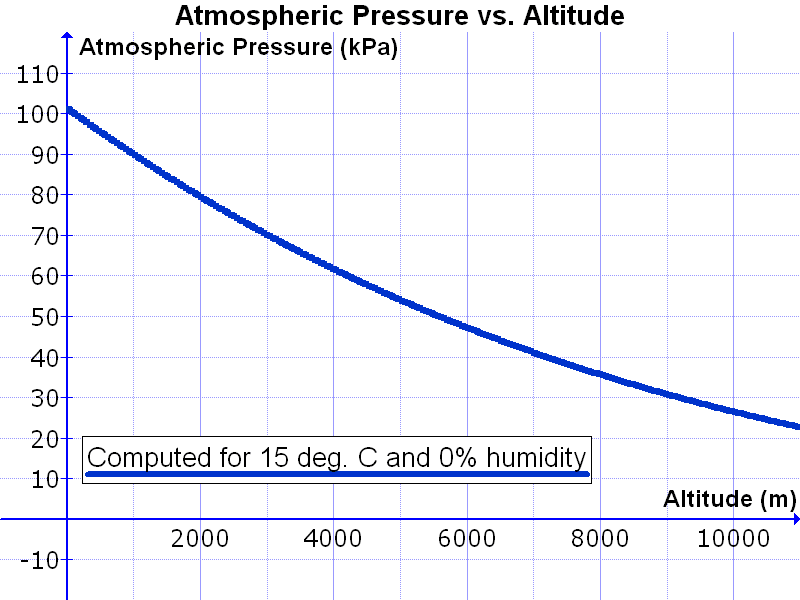
图 1：根据式 8 以及分压定律得到的大气压强随高度变化图，假设大气中没有水蒸气且温度恒定（来自维基百科）

　　现实中观测到大气温度随高度的增加而会发生变化，因此不能将大气简单地视为处于平衡态的热力学系统，这其中涉及到非平衡态的热力学机制。下面我们将构建两个较好的理论模型：等温大气模型和干绝热大气模型。湿绝热大气模型能够更好地解释大气温度随高度变化的一些现象（例如一座高山的顺风面和背风面可能存在温差），这在气象学中是很重要的一个理论：湿绝热方程。

1. 等温大气模型

　　¹以下介绍一个理想模型。假设大气是理想气体，密度随高度变化为 $\rho(z)$。所以高度 $z$ 处压强为

\begin{equation} P(z) = \int_{z}^\infty \rho(z') g \,\mathrm{d}{z'} ~. \end{equation}

其中由于大气厚度远小于地球半径，我们取 $g$ 为常数。根据理想气体状态方程，

\begin{equation} PV = n R T~. \end{equation}

先假设大气只是由一种分子构成，摩尔质量为 $\mu$，即 $m = n\mu$，代入有

\begin{equation} P = \frac{m}{\mu V} RT = \frac{R}{\mu} \rho T~, \end{equation}

其中 $P, T, \rho$ 都是高度的函数。代入式 1 得关于 $\rho(z)$ 的积分方程

\begin{equation} \frac{R}{\mu} \rho(z) T(z) = \int_{z}^\infty \rho(z') g \,\mathrm{d}{z'} ~. \end{equation}

通常来说海拔越高的地方气温越低，如果 $T(z)$ 是已知的，就可以解出 $\rho(z)$。方程两边对 $z$ 求导，整理得

\begin{equation} \rho'(z) + \frac{1}{T(z)} \left[T'(z) + \frac{\mu g}{R} \right] \rho(z) = 0~. \end{equation}

这是一个一阶线性微分方程，可以直接用公式求解。把解出的 $\rho(z)$ 代入式 3 即可求出对应的压强 $P(z)$。

　　作为一种简单情况，假设温度不随高度变化（实际上，空气的热导率很小，考虑成绝热过程能得到更加精确的结果式 16 ），那么方程变为常系数的

\begin{equation} \rho'(z) + \frac{\mu g}{RT}\rho(z) = 0~, \end{equation}

容易解得

\begin{equation} \rho(z) = \rho_0 \exp\left(-\frac{\mu g}{RT} z\right) ~, \end{equation}

或者

\begin{equation} P(z) = P_0 \exp\left(-\frac{\mu g}{RT} z\right) ~, \end{equation}

其中 $\rho_0, P_0$ 是某个高度 $z_0$ 处的大气密度和气压。这说明恒温条件下气压随海拔升高呈指数下降，且温度越低下降越快。

　　当大气中有多种气体时，可以对每种气体分别求解，把 $P_0$ 替换为改气体在 $z_0$ 处的分压。总密度就是每种气体的密度之和。大气中的水蒸气同样也可能随着高度变化。

2. 干绝热大气模型

　　假设大气是理想气体，其热导率很小，所以大气的对流过程可以近似考虑成绝热过程（实验表明随着高度的增加大气温度下降，这说明不宜用等温大气模型），即

\begin{equation} \begin{aligned} &\begin{cases} &PV_m^\gamma=C\\ &V_m=\frac{RT}{P},P=\frac{\rho R T}{\mu} \end{cases} \\ &\Rightarrow \rho^{1-\gamma}T=C'\\ &\Rightarrow (1-\gamma)T \,\mathrm{d}{\rho} +\rho \,\mathrm{d}{T} =0 ~, \end{aligned} \end{equation}

那么式 5 变为

\begin{equation} \frac{\gamma}{\gamma-1}T'(z)=-\frac{\mu g}{R}~. \end{equation}

积分得²

\begin{equation} \begin{aligned} T&=T_0-\int_{z_0}\frac{\gamma-1}{\gamma}\frac{\mu g}{R} \,\mathrm{d}{z} \\&\approx T_0\left[1-\frac{\gamma-1}{\gamma}\frac{\mu g}{R T_0}z\right]~,\\ P&=P_0\left[1-\frac{\gamma-1}{\gamma}\frac{\mu g}{R T_0}z\right]^{\gamma/(\gamma-1)}~. \end{aligned} \end{equation}

温度 $T$ 总是 $>0$ 的，且大气的绝热指数 $\gamma>1$，这意味着温度随高度的增加而降低。可以利用气体热容量公式式 9 约去 $\gamma$，积分得：

\begin{equation} T=T_0-\int_{z_0}\frac{\mu g}{c_{p,m}} \,\mathrm{d}{z} ~, \end{equation}

　　 $\mu,c_{p,m}$ 可近似看成常数。大气的摩尔质量为 $29 \rm{g\cdot mol^{-1}}$，摩尔定压热容约为 $29 \rm{J\cdot mol^{-1}K^{-1}}$，因此计算得

\begin{equation} \begin{aligned} &T=T_0-\frac{\mu g}{c_{p,m}} z~,\\ &T\approx T_0-z\cdot 10 \rm{K/km}~. \end{aligned} \end{equation}

即每升高一千米，温度降低约 $10$ 摄氏度。该数值称为干绝热递减率。

1. ^ 参考 Wikipedia 相关页面以及另一个页面。
2. ^ 并且可以验证，当 $\gamma$ 趋近于 $1$ 时，下面的方程就变为等温模型的大气压强公式。