光的多普勒效应

贡献者： JierPeter; addis; _Eden_

预备知识　多普勒效应，洛伦兹变换

　　约定采用自然单位制，即 $c=1$。

　　不论是牛顿力学框架下还是相对论意义下，光的频率都可能在不同参考系之间有所不同。由于观察者和光源之间相对运动，造成观察者所测得的光的频率与光源的频率不一致，这个现象被称为光的多普勒效应。由于光速不变原理，在相对论框架下讨论光的多普勒效应反而更为简单。

1. 光的多普勒效应的推导

　　由于在任何参考系中，光的速度都一样，因此只需要知道光的波长就可以根据以下公式得到光的频率：

\begin{equation} f=\frac{1}{\lambda}~. \end{equation}

其中，$f$ 是光的频率，$\lambda$ 是光的波长，$1$ 是光速。

　　假设光源所在的参考系为 $K_1$，观察者所在的参考系为 $K_2$，而 $K_2$ 相对 $K_1$ 的运动速度为 $\vec{v}=(v, 0, 0)^T$。设光的频率在 $K_1$ 为 $f$，在 $K_2$ 中为 $f'$，那么光的波长在 $K_1$ 中为 $\lambda=1/f$，在 $K_2$ 中为 $\lambda'=1/f'$。

一维情况

　　设在 $K_1$ 看来，观察者和光的运动方向是一致的，即观测者以 $v$ 的速度背离光源运动。

　　取 $K_1$ 中光的两个相邻的波峰¹，作为两个以光速运动的点。为简化讨论，不妨设其中一个点的世界线²表示为

\begin{equation} \begin{pmatrix}t_1\\t_1\\0\\0\end{pmatrix} ~, \end{equation}

而另一个点为

\begin{equation} \begin{pmatrix}t_2\\t_2+\lambda\\0\\0\end{pmatrix} ~. \end{equation}

　　代入洛伦兹变换可得，在 $K_2$ 中两波峰的世界线分别为

\begin{equation} \begin{pmatrix}\frac{t_1-vt_1}{\sqrt{1-v^2}}\\\frac{t_1-vt_1}{\sqrt{1-v^2}}\\0\\0\end{pmatrix} ~, \end{equation}

和

\begin{equation} \begin{pmatrix}\frac{t_2-v(t_2+\lambda)}{\sqrt{1-v^2}}\\\frac{(t_2+\lambda)-vt_2}{\sqrt{1-v^2}}\\0\\0\end{pmatrix} = \begin{pmatrix}\frac{t_2-vt_2-v\lambda}{\sqrt{1-v^2}}\\\frac{t_2-vt_2+\lambda}{\sqrt{1-v^2}}\\0\\0\end{pmatrix} ~. \end{equation}

　　在各参考系中计算波长，就要计算对应参考系中同一时间下两波峰的空间坐标的差。对于 $K_1$，“同一时间” 意味着 $t_1=t_2$；对于 $K_2$，“同一时间” 意味着 $t_1-vt_1=t_2-v(t_2+\lambda)$，

　　将 “同一时间” 条件分别代入两个参考系中两个点的世界线，消去 $t_1$ 计算后发现，两波峰在 $K_1$ 中的距离始终是 $\lambda$，而在 $K_2$ 中的距离始终是 $\frac{(1+v)\lambda}{\sqrt{1-v^2}}$。由于已经设定这束光在 $K_2$ 中的波长是 $\lambda'$，因此有

\begin{equation} \lambda'=\frac{(1+v)\lambda}{\sqrt{1-v^2}}=\frac{\sqrt{1+v}}{\sqrt{1-v}}\lambda~. \end{equation}

　　因此在 $K_2$ 中，光的频率变为

\begin{equation} f'=\frac{1}{\lambda'}=\frac{\sqrt{1-v}}{\sqrt{1+v}\lambda}=\frac{\sqrt{1-v}}{\sqrt{1+v}}f~. \end{equation}

　　这就是一维情况下光的多普勒效应。对于背离光源运动的观测者来说，光的频率发生了红移（$f'< f$）。

三维情况

　　三维情况下，可以预料在 $K_1$ 看来光的传播方向和在 $K_2$ 参考系看来的运动方向不一致的情况。因此情况会较为复杂，我们需要考虑新的方法。

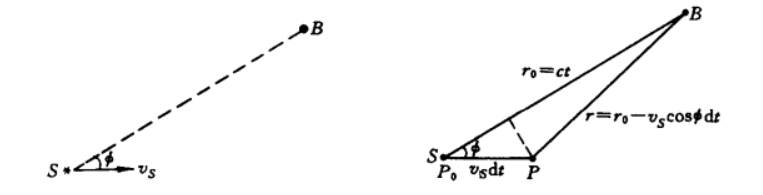
　　考察图 1 的情况，我们直接在$K_2$ 参考系中进行分析，不妨假设光源 $S$ 正以 $v$ 的速度沿 $x$ 轴正方向运动，并且在 $K_2$ 参考系看来在 $t$ 时刻接收到的电磁波方向与 $x$ 轴成 $\phi$ 角（注意这个角度是在 $K_2$ 参考系测得的）。

图 1：多普勒效应示意图（参考舒幼生力学 [1] 8.3.2 节例 11 的图）

　　假设在 $0$ 时刻光源位于 $P_0$ 点，它发出的电磁波于 $t$ 时刻被 $B$ 点处的观测者接收到，并且观测者测得的电磁波方向与 $x$ 轴夹角为 $\phi$。那么 $S$ 到 $B$ 的距离为 $r_0=ct=t$（自然单位制下 $c=1$）。而经过 $ \,\mathrm{d}{t} $ 的时间后光源移动到了 $P$ 点的位置，在这段时间内光源所经历的固有时（也就是 $K_1$ 参考系中光源所经历的原时）为 $ \,\mathrm{d}{t} /\gamma=\sqrt{1-v^2} \,\mathrm{d}{t} $（即钟慢效应），因此在这段时间内光源 “振动” 的次数为

\begin{equation} N'=f\cdot \gamma \,\mathrm{d}{t} = f\sqrt{1-v^2} \,\mathrm{d}{t} ~, \end{equation}

现在考虑光源在 $P$ 点处发出的电磁波在什么时刻被 $B$ 点接受到。如图所示，$P$ 到 $B$ 的距离为

\begin{equation} r=r_0-v\cos\phi \,\mathrm{d}{t} =t-v\cos\phi \,\mathrm{d}{t} ~, \end{equation}

这也就意味着光源从 $P$ 发出的电磁波经过了 $r/c=r$（自然单位制下 $c=1$）的时间被 $B$ 点的观测者接收到。经过计算，可以看到 $P_0$ 点发出的电磁波与 $P$ 点发出的电磁波被 $B$ 点观测者接收到的时间差为

\begin{equation} \,\mathrm{d}{t} ' = \,\mathrm{d}{t} + r - t = \,\mathrm{d}{t} -v\cos\phi \,\mathrm{d}{t} ~. \end{equation}

因此根据式 8 和式 10 ，$K_2$ 参考系中 $B$ 点观测者观测到的光的频率为

\begin{equation} f'=\frac{N'}{ \,\mathrm{d}{t} '}=\frac{\sqrt{1-v^2}}{1-v\cos\phi} f~. \end{equation}

　　这就是三维空间中一般情况下光的多普勒效应。如果 $\phi=0$ 或 $\phi=\pi$，那么情况退化为一维空间的问题。作为验证将 $\phi=\pi$ 代入式 11 后结果和式 7 一致，这种情况对应于光源背离观测者运动（或观测者背离光源运动）的情况。

　　另一个更具数学技巧和简洁性的推导是利用了波四矢 $k^\mu$ 的变换规则，具体过程见狭义相对论运动学（无质量粒子）。

1. ^ 也可以是相邻波谷，或者任何相邻的两个同相位的点。
2. ^ 见时空的四维表示或世界线和固有时。

[1] ^ 舒幼生. 力学第一版