狭义相对论的运动学(无质量粒子和多普勒效应)
贡献者: _Eden_
约定使用东海岸度规 $\eta_{\mu\nu}=\rm{diag}(-1,1,1,1)$ 和自然单位制 $c=\hbar=1$。
1. 四速度、四动量、波四矢量
对于无质量粒子,它的世界线为类光世界线,$V^\mu= \,\mathrm{d}{x} ^\mu(\lambda)/ \,\mathrm{d}{\lambda} $ 满足 $V^\mu V_\mu = 0$。我们无法用固有时对类光世界线进行参数化,因为在类光世界线上的任意两点的时空间隔都为 $0$。那么我们只能寻求其他的参数化方式。在狭义相对论中,无质量粒子不会受到力的作用,因此其四速度是恒定的,世界线在时空中是一条直线。例如以下就是一条无质量粒子的世界线:
\begin{equation}
x^\mu(\lambda)=b^\mu \lambda,\quad b^\mu=(1,1,0,0)~,
\end{equation}
无质量粒子的能量与波的频率 $\omega$ 成正比,动量与波数 $ \boldsymbol{\mathbf{k}} $ 成正比,即德布罗意关系。那么可以定义其四动量为
\begin{equation}
p^\mu=(E, \boldsymbol{\mathbf{P}} )=(\hbar \omega,\hbar \boldsymbol{\mathbf{k}} )=\hbar k^\mu~,
\end{equation}
\begin{equation}
\hat p,\hat k \propto \hat V= \frac{\mathrm{d}{\hat x(\lambda)}}{\mathrm{d}{\lambda}} ~,
\end{equation}
\begin{equation}
p^\mu p_\mu = E^2-| \boldsymbol{\mathbf{P}} |^2=\omega^2-| \boldsymbol{\mathbf{k}} |^2=0~.
\end{equation}
2. 多普勒效应
考虑一个光源,在它的参考系中光子沿各个方向以频率 $\omega$ 发射。而对于接收器,假设它相对于光源以速度 $ \boldsymbol{\mathbf{v}} =-v \hat e_x$ 运动($v>0$ 代表相向,$v<0$ 代表背向运动)。
假设在光源参考系 $S$ 中,以 $\alpha$ 角发射的光子被接收器接收到。那么 假设在观测者静止的参考系 $S'$ 中,在观测者眼中光子是以 $\alpha'$ 角接收到的,即观测到的光子具有波四矢量
\begin{equation}
k'^\mu = \frac{2\pi}{\lambda'}(1,\cos\alpha',\sin\alpha',0)~,
\end{equation}
那么可以通过一个 $ \boldsymbol{\mathbf{v}} $ 方向的洛伦兹变换
\begin{equation}
\Lambda^\mu{}_\nu=\begin{pmatrix}
\gamma & -v\gamma & & \\
-v\gamma & \gamma & & \\
& & 1 & \\
& & & 1
\end{pmatrix}~.
\end{equation}
\begin{equation}
k^\mu = \Lambda^\mu{}_\nu k'^\nu = \frac{2\pi}{\lambda}(1,\cos\alpha,\sin\alpha,0)~,
\end{equation}
\begin{equation}
\begin{aligned}
& \gamma\cdot\frac{2\pi}{\lambda'}\left(1-v\cos\alpha'\right)=\frac{2\pi}{\lambda}~,\\
& \gamma\cdot\frac{2\pi}{\lambda'}\left(\cos\alpha'-v\right)=\frac{2\pi}{\lambda}\cos\alpha~,\\
& \frac{2\pi}{\lambda'}\sin\alpha' = \frac{2\pi }{\lambda}\sin\alpha~.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
&\frac{\lambda'}{\lambda}=\gamma(1-v\cos\alpha')~,\\
&\tan\alpha=\frac{\tan\alpha'}{\gamma(1-v\sec \alpha')}~.
\end{aligned}
\end{equation}
\begin{equation}
\nu'=\frac{\nu}{\gamma(1-v\cos\alpha')}~.
\end{equation}
证明:
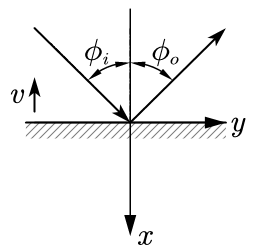
图 1:习题 1 示意图
设平面镜参考系(相对于实验室参考系以 $v$ 的速度向 $-x$ 方向运动)下入光的波四矢为
\begin{equation}
k'_i{}^\mu=\nu'(1,\cos\theta',\sin\theta',0)~.
\end{equation}
\begin{equation}
k'_o{}^\mu=\nu'(1,-\cos\theta',\sin\theta',0)~.
\end{equation}
\begin{equation}
\begin{aligned}
k_i&=\Lambda^\mu{}_\nu k'_i{}^\nu=\nu'(\gamma(1-v\cos\theta'),\gamma(\cos\theta'-v),\sin\theta',0)\\
&=\nu_i(1,\cos\phi_i,\sin\phi_i,0)~,\\
k_o&=\Lambda^\mu{}_\nu k'_o{}^\nu=\nu'(\gamma(1+v\cos\theta'),\gamma(-\cos\theta'-v),\sin\theta',0)\\
&=\nu_o(1,-\cos\phi_o,\sin\phi_o,0)~.
\end{aligned}
\end{equation}
\begin{equation}
\frac{\nu_o}{\nu_i}=\frac{\sin\phi_i}{\sin\phi_o}~.
\end{equation}
\begin{equation}
\begin{aligned}
\tan\left(\theta_i/2\right) &=\frac{\nu_i\sin\theta_i}{\nu_i\cos\theta_i+\nu_i}=\frac{\nu'\sin\theta'}{\nu'\gamma(\cos\theta'-v)+\nu'\gamma(1-v\cos\theta')}\\
&=\frac{\sin\theta'}{\gamma(1-v)(1+\cos\theta')}~.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\tan\left(\theta_o/2\right) &=\frac{\nu_o\sin\theta_o}{\nu_o\cos\theta_o+\nu_o}=\frac{\nu'\sin\theta'}{\nu'\gamma(\cos\theta'+v)+\nu'\gamma(1+v\cos\theta')}\\
&=\frac{\sin\theta'}{\gamma(1+v)(1+\cos\theta')}~.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
\frac{\tan\frac{1}{2}\phi_i}{\tan\frac{1}{2}\phi_o}=\frac{1+v}{1-v},\quad \frac{\nu_o}{\nu_i}=\frac{\sin\phi_i}{\sin\phi_o}~.
\end{aligned}
\end{equation}