贡献者: addis; ACertainUser; Giacomo
预备知识 数列的极限(极简微积分)
,充分必要条件
,函数(高中)
1. 引入
我们先通过简单的例子初步了解函数的极限。
例 1
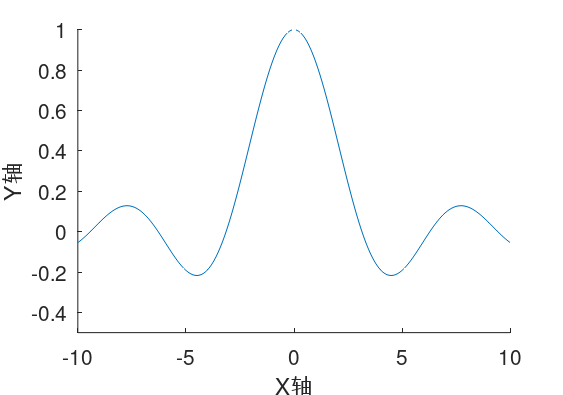
图 1:$f(x)=\frac{ \sin\left(x\right) }{x}$ 的图像
思考一下 $f(x)=\frac{ \sin\left(x\right) }{x}$ 这一经典函数在原点附近的值。
众所周知,当 $x=0$ 时,由于分母为 $0$,该分数没有意义;但当 $x$ 趋近于 $0$,如分别令 $x=0.1,x=0.01,...$ 而不等于 $0$ 时,有趣的事情发生了:如图 1 和表 1 所示,此时分数的值似乎趋于一个确定的值 $1$.
表1:x 与 f(x)
|
$x$ | $0.1$ | $0.01$ | $0.001$
|
|
$f(x)$ | $0.9983$ | $0.99998$ | $0.9999998$
|
看起来,尽管我们不能定义 $f(x)$ 在零点处的值,但是我们知道,当 $x$ 趋近于 $0$ 时,$f(x)$ 趋近于 $1$. 因此,我们说 $\lim\limits_{x\to0}\frac{ \sin\left(x\right) }{x}=1$
例 2
图 2:$f(x)=1/x$ 的图像 (x>0)
然后,我们再看看 $f(x)=1/x$ 另一经典函数的图像。我们还是知道,两个正数相除始终大于零;但当 $x$足够大时,$1/x$ 会足够小以至趋于 $0$. 因此,我们说 $\lim\limits_{x\to+\infty}1/x=0$。
2. 自变量趋于无穷的极限
实函数 $f(x)$ 可以看成是一种 “连续” 的数列,只不过把元素编号从离散的 $n$ 改为连续的 $x$。类比数列的极限,我们也可以定义函数趋于正无穷的极限。
定义 1 函数趋于正无穷的极限
考虑实函数 $f(x)$。若无论要求 $f(x)$ 和一确定实数 $A$ 的距离 $\epsilon$ 有多小(但 $\epsilon>0$),都存在实数 $X$,使得所有 $x>X$ 都满足 $ \left\lvert f(x)-A \right\rvert <\epsilon$,那么我们说 $A$ 是函数 $f(x)$ 在 $x$ 趋于正无穷时的极限,记为
\begin{equation}
\lim\limits_{x\to +\infty} f(x) = A~.
\end{equation}
可以看到该定义和数列极限的定义(定义 1 )非常相似,只是简单做了替换。不过,函数并不是简单地把数列的概念拓展到连续的情况。数列的编号只能朝着一个方向增大,但函数的自变量 $x$ 既可以趋近正无穷也可以奔向负无穷,
图 3:对于任意一个 $\epsilon$,都存在对应的 $X$。仿自
[1]
习题 1
请仿照定义 1 给出函数趋于负无穷时极限的定义
\begin{equation}
\lim\limits_{x\to -\infty} f(x) = A~.
\end{equation}
注意 $\lim\limits_{x\to\infty} f(x) = A$ 仅表示正无穷的极限而不是两个方向的极限都是 $A$。
3. 自变量趋于一点的的极限
另外,由于 $x$ 是连续取值的,也可以考察自变量 $x$ 不断趋近某一点 $x_0$ 的极限,即 $x\to x_0$。如何描述 “自变量趋于一个给定的实数 $x_0$” 呢?只需要取自变量 $x$ 使得二者间的距离 $ \left\lvert x-x_0 \right\rvert $ 越来越接近 $0$ 即可。
定义 2 函数在某点的极限
考虑实函数 $f(x)$。若无论要求 $f(x)$ 和确定实数 $A$ 的距离 $\epsilon>0$ 有多小,都存在一个自变量的取值半径 $\delta>0$,使得对任意满足 $ \left\lvert x-x_0 \right\rvert < \delta$ 的实数 $x$,都有 $ \left\lvert f(x)-A \right\rvert <\epsilon$,
那么我们说 $A$ 是函数 $f(x)$ 在 $x$ 趋于 $x_0$ 时的极限,记为
\begin{equation}
\lim\limits_{x\to x_0}f(x)=A~.
\end{equation}
图 4:对于任意一个 $\epsilon$,都存在对应的 $\delta$.仿自
[1]
例 3 简单技巧
求一些简单的函数在某个值处的极限时,通常可以直接代入数值计算(如果存在的话),如
\begin{equation}
\lim_{x\to 1} 2x + 1 = 3 ~,\qquad \lim_{x\to 2}\frac{x + 1}{x + 2} = \frac34~.
\end{equation}
当无穷大与常数相加时,可以忽略常数,如
\begin{equation}
\lim_{x\to +\infty} \frac{x + 1}{2x + 2} = \lim_{x\to +\infty} \frac{x}{2x} = \frac12~.
\end{equation}
我们可以换个角度计算上面的极限,
\begin{equation}
\lim_{x\to +\infty} \frac{x + 1}{2x + 2} = \lim_{x\to +\infty} \frac{1 + 1/x}{2 + 2/x} = \frac12~.
\end{equation}
$1/x$ 和 $2/x$ 是 “无穷小”,因此可以忽略。
这个技巧来源于一个事实:那些 “简单函数” 通常都是 “连续” 的,或者说,至少在所需求极限的那个点附近是 “连续” 的:它们的图像在自变量所趋向的值附近是一条连续不断的曲线。有关这点,更详细的信息请参考专门的词条。
如果你想要处理更复杂的极限问题,那你可以参考求极限的一些方法。不过,其中部分方法已经超出了初学者的(以及 “极简微积分” 的)知识范围。
左、右极限
我们还可以区分函数在某点的左极限(left limit)和右极限(right limit)。简而言之就是 $x$ 分别从左边和右边两个方向趋近 $x_0$ 时的极限,具体定义留做思考。左右极限记为
\begin{equation}
\lim_{x\to x_0^-} f(x) = A_- ~,\qquad \lim_{x\to x_0^+} f(x) = A_+~.
\end{equation}
定理 1
函数在某点存在极限的充分必要条件是它左右极限都存在并相等。
$$\lim_{x\to x_0} f(x) = A \Leftrightarrow \lim_{x\to x_0^-} f(x) = \lim_{x\to x_0^+} f(x) = A ~.$$
也就是说,若左(或右)极限不存在,或者左右极限存在但不相等,那此处的极限就不存在。
例 4
图 5:函数 $\theta(x)$ 的图像
函数
\begin{equation}
\theta(x) = \left\{\begin{aligned}
0 \qquad (x < 0)\\
1 \qquad (x \ge 0)
\end{aligned}\right. ~.\end{equation}
计算左极限 $\lim\limits_{x\to x_0^-} \theta(x)$ 时,假定 x 从左侧不断接近 $0$($x=-0.1,x=-0.01,...$),但从不超过(也不等于)$0$。此时总有 $x<0$,因此 $\lim\limits_{x\to x_0^-} \theta(x) = 0$.
同理,$\lim\limits_{x\to x_0^+} \theta(x) = 1~.$
由于左右极限不相同,因此 $\theta(x)$ 在 $x=0$ 处的极限不存在。
某点处函数的极限值与函数值
新手最常犯的错误莫过于过度纠结某处的函数极限值 $\lim\limits_{x\to x_0} f(x)$ 与函数值 $f(x_0)$ 的联系。事实上,这两者之间没有必要的关联1。$f(x_0)$ 可以不等于 $\lim\limits_{x\to x_0} f(x)$,$f(x)$ 甚至可以在 $x_0$ 处没有定义。总之,某处的函数极限值并不依赖于该点处的函数值。
这是因为定义中只考虑 $x$ 慢慢接近 $x_0$ 的过程,而不考虑 $x = x_0$ 的情况。即使我们把这点从函数定义域中挖去,极限是否存在,以及极限值是多少都不会被改变。例如在例 1 与在 “小角极限” 中会看到,虽然 $\sin x/ x$ 在 $x = 0$ 处没有定义,但其极限却等于 $1$。
例 5 可去间断点
图 6:函数 f(x)的图像
函数
\begin{equation}
f(x) = \left\{\begin{aligned}
x \qquad (x \ne 1)\\
1.5 \qquad (x = 1)
\end{aligned}\right. ~.\end{equation}
计算 $\lim\limits_{x\to 1} f(x)$ 时,由于只考虑 $x=1$ 附近的情况、而不考虑 $x=1$ 本身的情况,因此 $\lim\limits_{x\to 1} f(x)$ 的结果与 $f(1)$ 的值无关。在本例中,$\lim\limits_{x\to 1} f(x)=1$, 而 $f(1)=1.5$。
4. 极限不存在
和数列的极限一样,如果一个函数 $f(x)$ 的某种极限不存在,就说该极限不收敛。但不收敛的情况也有不同的细分。
如果在一个极限中,函数值趋于正无穷或负无穷2,则记为
\begin{equation}
\lim\limits_{x\to \square} f(x) = \pm\infty~.
\end{equation}
其中 $+\infty$ 可以简记为 $\infty$。注意术语上不能说该极限
存在且等于无穷,因为该极限是不存在的,存在就意味着等号右边是一具体的数。
例 6
式 10 并不是极限不存在的唯一一种情况,例如 $\lim\limits_{x\to\pm\infty}\sin x$ 和 $\lim\limits_{x\to 0} \sin\left(1/x\right) $ 的极限同样不存在,但不满足式 10 。
1. ^ 对于连续函数,才有 $\lim\limits_{x\to x_0} f(x)=f(x_0)$。然而,大多数常见的函数都是连续函数,这使得这个问题更具迷惑性
2. ^ 如果要严格定义式 10 ,就用 $\delta$-$\epsilon$ 语言,例如:对任意给定的 $A > 0$ 总存在……,当……就有 $f(x) > A$。
[1] ^ J. Hass, C. Heil, M. Weir.Thomas' Cauculus 14ed