贡献者: addis; Connection; JierPeter; Giacomo; 欄、停敘
微积分的核心概念是极限(limit),常见的极限有数列的极限以及函数的极限。数列是离散的,比较容易理解。事实上,数列就是一种特殊的函数(定义域为 $N^{*}$)。
我们通过一些例子引入。
例 1 圆周率
我们知道 $\pi$ 是一个无理数,所以 $\pi$ 的小数部分是无限多的。目前用计算机已经可以将 $\pi$ 精确地计算到小数点后数亿位。然而在实际应用中,往往只用取前几位小数的近似即可。下面给出一个数列,定义第 $n$ 项是 $\pi$ 的前 $n$ 位小数近似(去尾),即
\begin{equation}
a_0 = 3,\,\, a_1 = 3.1,\,\, a_2 = 3.14,\,\, a_3 = 3.141,\,\dots~
\end{equation}
显而易见,当 $n$ 趋于无穷时,$a_n$ 趋于 $\pi$。无穷(infinity)用符号 $\infty$ 来表示。我们说该数列的极限值是 $\pi$,也可以简称极限(limit)。以上这种情况,用极限符号表示,就是
\begin{equation}
\lim_{n \to \infty } {a_n} = \pi ~.
\end{equation}
这里 $\lim$ 是极限的数学符号,下方用箭头表示某个量 “无止境” 变化的过程。对于数列而言,唯一的 “无止境” 变化就是项标 $n$ 不断增加。
$\lim\limits_{n \to \infty }$ 在这里相当于一个 “操作”,叫做算符(operator)。它作用在整个数列上,并输出一个数,也就是数列的极限值。这有些类似于函数输入一个自变量并输出一个函数值,只不过 $\lim$ 算符的自变量从数换成了数列。所以不要误以为式 2 是说当 $n = \infty$ 时,有1 $a_n=\pi$,而要理解成数列 $a_n$ 经过算符 $\lim\limits_{n \to \infty }$ 的作用以后,得出的结果是 $\pi$。类比函数 $\sin x = y$,是说 $x$ 经过正弦函数作用后等于 $y$。所以从概念上来说,极限中的 “趋于” 和 “等于” 是不同的。趋于是数列整体的性质,而不是某一个项性质。
我们可以总结出以上数列的一个性质,并把它作为数列极限的一般定义。具有极限的数列最显著的特征是,随着 $n$ 增加,后面的所有项都越来越接近极限值。可是一个难点在于如何定义 “越来越接近”。先看一个错误的理解:考虑数列
\begin{equation}
a_1 = 3.21,\ a_2 = 3.201,\ a_3 = 3.2001,\ a_4 = 3.20001, \dots~
\end{equation}
这个数列也同样越来越接近 $\pi$,但直觉告诉我们,它的极限是 $3.2$ 而不是 $\pi$。
既然要讨论有多接近,那就要定义距离。我们可以把第 $a_n$ 和极限值 $\pi$ 的距离用绝对值定义为 $ \left\lvert a_n - \pi \right\rvert $。对式 1 的数列,可以发现这个距离不光是越来越小,而且想要多小就有多小。例如要求 $ \left\lvert a_n - \pi \right\rvert < 10^{-2}$,容易发现 $n > 1$ 时就总能满足;又例如要求 $ \left\lvert a_n - \pi \right\rvert < 10^{-10}$,容易发现 $n > 9$ 时就总能满足;一般地如果要求 $ \left\lvert a_n - \pi \right\rvert < 10^{-q}$($q$ 为整数),只要 $n > q-1$ 就总能满足,这就意味着 $\lim\limits_{n \to \infty } a_n = \pi$。
有了这个定义,我们就可以轻易地判断式 3 的极限不是 $\pi$。因为无论 $n$ 为多大,总是有 $ \left\lvert a_n - \pi \right\rvert > 3.2 - \pi > 0.05$,所以如果要求一个比这更小的距离,那么就没有任何 $n$ 可以满足。
定义 1 数列的极限
考虑无穷项的实数数列 $a_1, a_2, \dots$,若存在一个实数 $A$,使得:无论多么小的正数 $\varepsilon$,总存在正整数 $N$,对任意 $n > N$ 都满足 $ \left\lvert a_n - A \right\rvert < \varepsilon$,则该数列的极限就是 $A$。
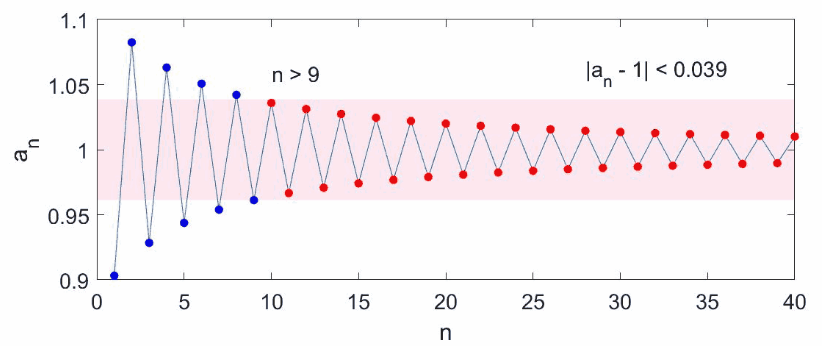
图 1:数列的极限(
查看动画):图中每点代表数列的一项,数列的极限值为 $1$,红色区域表示对距离 $ \left\lvert a_n - A \right\rvert $ 的要求,满足要求的 $a_n$ 为红色,不满足的为蓝色。无论红色区域有多窄(只要不为零),总能找到一个不等式 $n > N$ 使之后所有的点都是红色。
我们来看几个简单的例题,加深一下印象。
例 2 根据定义证明对数列 $\displaystyle a_n= {(-1)^n}{1\over{2^n}}$,$\lim\limits_{n\to\infty}a_n=0$
证明:
对任意 $\varepsilon$,取 $N=[-\log_2\varepsilon]$,则 $n>N$ 时有
$n>-\log_2\varepsilon$,即 $2^{-n}<\varepsilon$。又 $|a_n-0|=2^{-n}$。
因此,对任意 $\varepsilon$,存在 $N=[-\log_2\varepsilon]$,使得当 $n>N$ 时,$|a_n-0|<\varepsilon$。根据定义有 $\lim\limits_{n\to\infty}a_n=0$。
一些数列不存在极限:
习题 1
考虑数列 $a_n = n$ 以及 $a_n=(-1)^n$。它们存在极限吗?
定义 2 数列的敛散性
如果一个数列不存在极限,就称它是发散(divergent)的。如果存在极限,则称它是收敛(convergent)的。
例 3
容易发现数列的极限和前面有限项的值都无关,例如把式 1 中的前 10 项都改成 $0$,那么该数列的极限仍然是 $\pi$。把前一万项改成 $0$ 也同理。
例 4
根据定义,数列极限也并不要求 $n\to \infty$ 时数列的项不能等于极限值,例如数列
\begin{equation}
b_0 = 3.3~,\,\, b_1 = 3.2~, \,\, b_2 = \pi~, \,\, b_3 = \pi~, \,\, b_n = \pi \;\; (n \ge 2)~.
\end{equation}
当 $n \ge 2$ 时所有的项都等于 $\pi$,那么根据
定义 1 他的极限显然也是 $\pi$。因为令 $n > 1$ 即可满足定义中对距离的任何限制。
例 5
注意存在极限的数列未必要求距离 $ \left\lvert a_n - A \right\rvert $ 是严格递减的,例如数列
\begin{equation}
\frac{1}{2},\;\; \frac{1}{4},\;\; \frac{1}{3},\;\; \frac{1}{5},\;\; \frac{1}{4},\;\; \frac{1}{6},\;\; \frac{1}{5},\;\; \frac{1}{7},\;\; \dots~
\end{equation}
的极限是 $0$。
1. ^ 有两个理由可以说明这种理解不正确:首先,按定义,每个 $a_n$ 都是有理数,而 $\pi$ 是无理数,所以不应该有任何一个 $a_n=\pi$;其次,$\infty$ 不是一个实数,不存在 $n=\infty$ 的说法。这里的 $n\to\infty$ 只是表示 $n$ 无限增加的过程。